基于经验分布的投资选择

万云倩,范爱华

(安徽工业大学数理科学与工程学院,安徽 马鞍山 243032)

1 引言

俗话说:不能把鸡蛋放在一个篮子里.经济人在股票市场进行投资,要选择适当的投资组合,其中心问题是在回报与风险之间进行权衡.Markowitz[1]提出把投资组合收益率的期望和方差分别作为回报和风险,提出了均值-方差模型.首次对不确定情况下投资组合选择提供了宝贵分析方法.文献[2]利用均值-方差模型讨论了投资者的最优投资策略.文献[3]通过构建投资组合进行应用分析,分析均值和方差变动对投资组合有效前沿曲线的变动情况以及该变动对实际投资活动的影响.文献[4]讨论完备标准动态金融市场中在允许投资组合条件下的概率准则问题.文献[5]利用罚函数法,对最小风险组合证券的非负投资比例系数进行研究.

在文献[6]中引入滑动平均.假设一个经济人在证券市场中进行投资,他在观察了一段时间之后,在an时刻做出决策开始投资,然后等待在未来某个时刻an+ϕ(n)时刻退出市场,此模型称之为滑动投资模型.最后,利用凸函数,函数连续性,泰勒级数,勒贝格控制收敛定理等方法,研究在这一模型下经济人的平均收益与期望收益之间的大样本性质.

2 基本概念与模型假设

定义 2.1[7]一个股票市场是由各只股票为分量组成的列向量:

上标T表示转置,

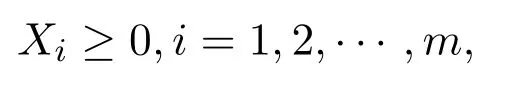
其中m是该股票市场中所有股票的只数,Xi称为相对价格,其为第i只股票当天的收盘价与开盘价之比.

定义 2.2[7]一个投资组合是列向量:

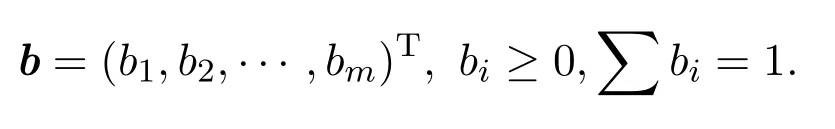
其实,它就是将资金如何按比例分散投资到各股上的分配方案,其中bi理解为某人投资第i只股票的资金占其总投资的比例.

定义 2.3[7]如果采用投资组合策略b,而股票向量为X,那么相对收益(指当天收盘时的总市值与开盘时的总市值之比)则为:

定义 2.4[6]若将流动资金进行再次分配,在第i次分配中,投资组合bi对股票向量X1,X2,···进行重复投资,那么重复n次之后获得的相对收益Sn为:

定义 2.5[6]考虑函数h(·):Rn → R∪{∞}.epih(·)表示集合{(y,α)∈ Rn×R:h(y)≤ α}.

定义 2.6[6]设B表示投资组合的集合,B∗表示对数最优投资组合的集合.

假设 1股票市场收益率向量X1,X2,···是独立同分布的.

假设 2股票的概率分布预先未知.

如果

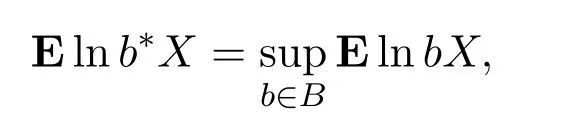
那么投资组合b∗被称为对数最优.由于投资组合选择可以依靠过去的结果,那么投资组合就可被描述成一列投资组合选择{bn(X1,X2,···,Xn−1)}∞n=1.

可测函数bn(X1,X2,···,Xn−1)的映射是从股票市场收益率向量的过去结果到投资组合的集合.表示为:

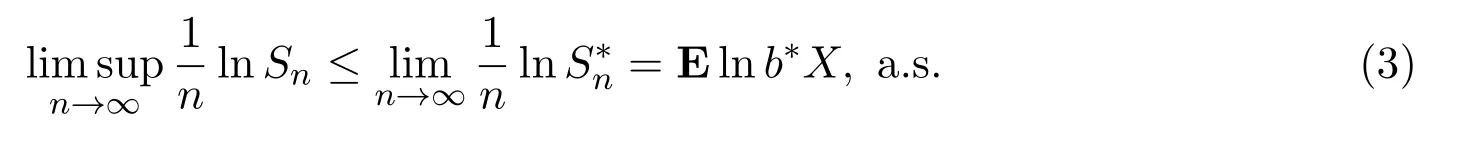
其中

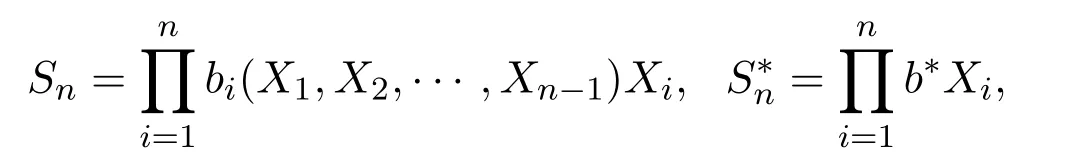
表示资金经过n次重复投资得到的投资选择和对数最优投资组合.由文献 [11]可知,是投资选择可得到的资本最优渐近增长率.

考虑一个可实现资本渐近最优增长率的目标,并寻找它的投资选择

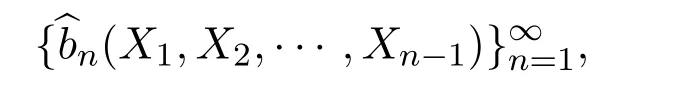
即

其中

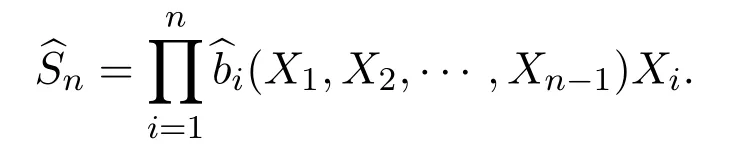
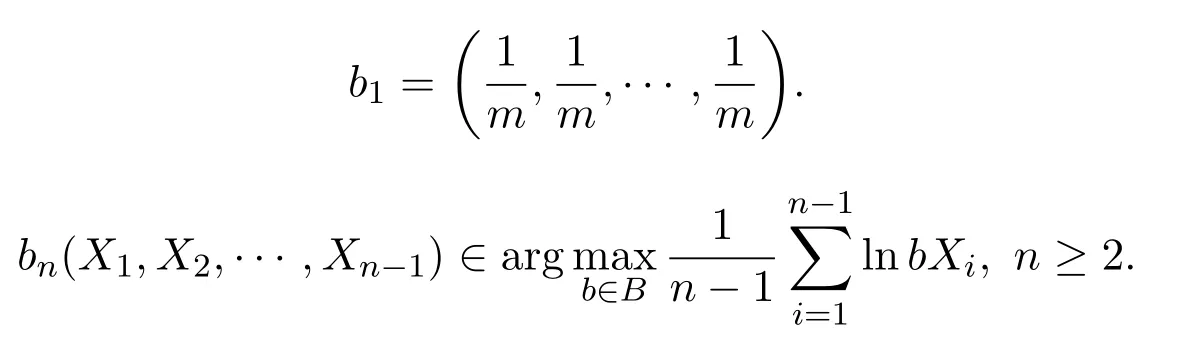
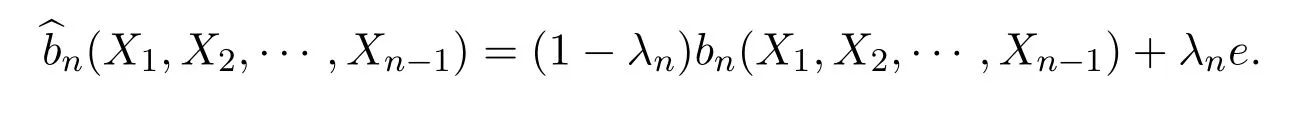
3 基本引理

引理 3.1设概率空间(Ω,D,P),其中 Ω=Rm,且D表示关于P的 Borelσ-代数,设 Φ表示集合:

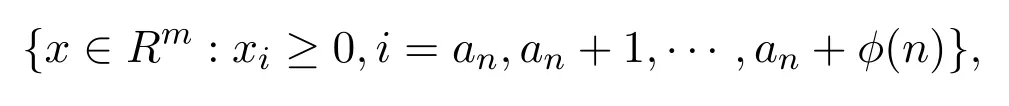
考虑函数

即f(·,·):Rm ×Ω→ R ∪ {∞},那么

1)∀x∈Ω,集合 epif(·,x)={(b,α)∈ Rm ×R:f(b,x)≤ α}是凸的.

2) 集合 epif(·,x) 是闭的.

3)对所有闭子集F ⊆Rm+1有{x∈Ω:epif(·,x)∩F ≠∅}∈D.

4)在乘积概率空间 (Ω(n),D(n),P(n))中,∀(xan,xan+1,···,xan+ϕ(n))∈Ω(n),集合是闭的.

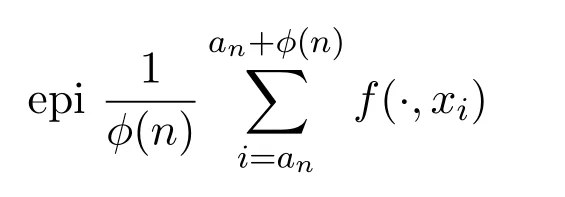
5)对所有闭子集F⊆Rm+1有

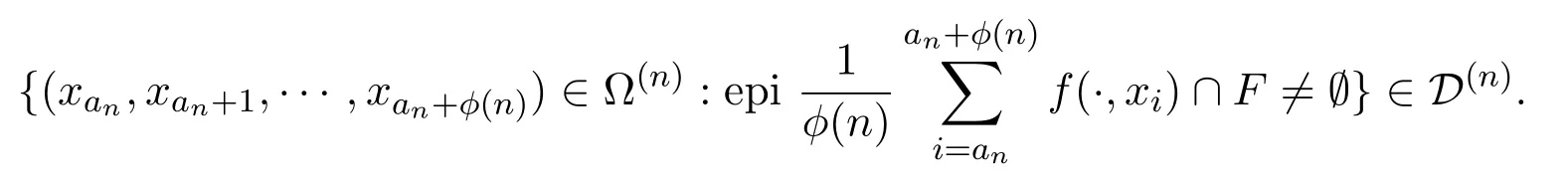
证明1),2),3)的证明参见文献[6].

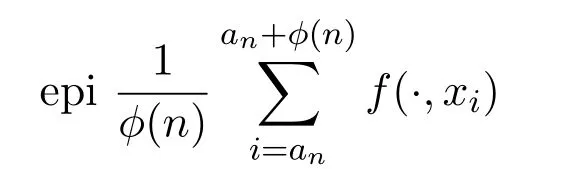
是空集.

假设 (xan,xan+1,···,xan+ϕ(n))∈Φ(n),若 (b′,α′) 是集合

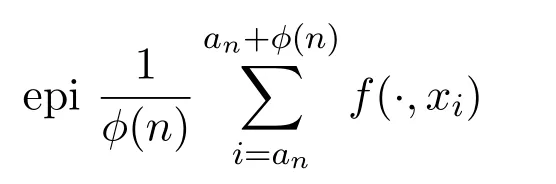
的边界,设 (bi,αi) 收敛于 (b′,α′),使得

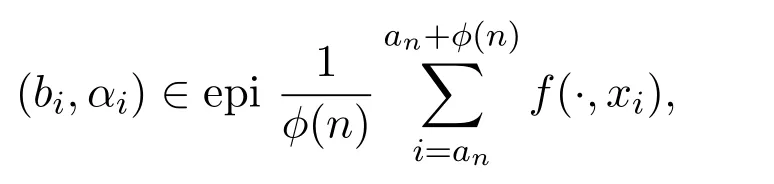
因此bi,b′∈Bn,αi,α′∈Rn.设∀ε＞0,当α′是有限的,且i足够大,那么

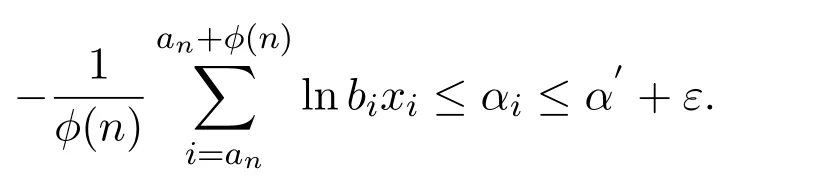
由函数−lnbx的连续性,

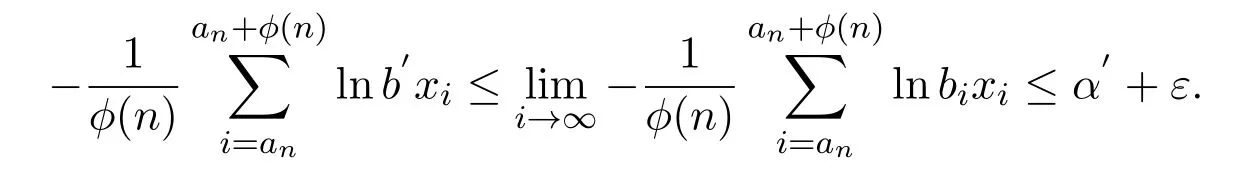
由于ε是任意的,那么

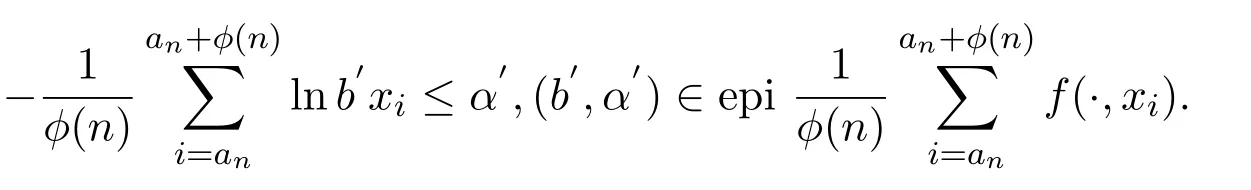
5)假设G是Rm+1的有界闭集,设

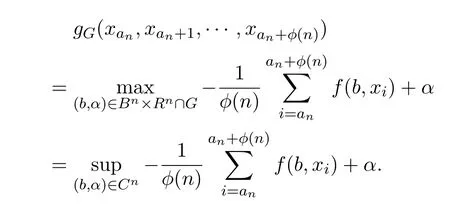
其中Cn是Bn×Rn∩G上的可数稠密子集,对每个b∈Bn,α∈Rn,函数

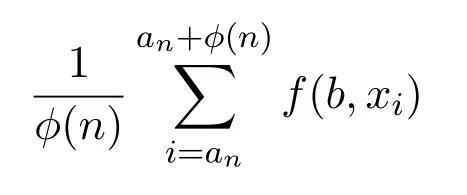
是可测的.

设F表示Rm+1的闭集,下列叙述都等价的:

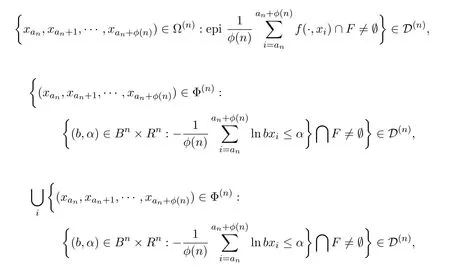
其中Fi是有界闭集(可数多个),使得

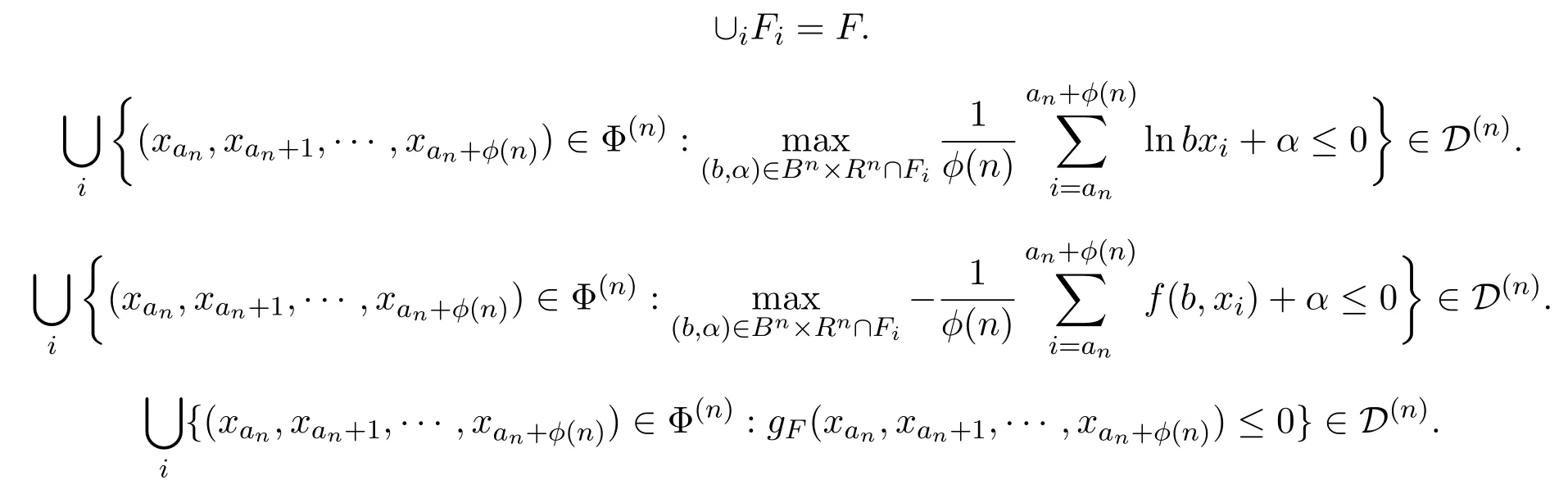
上述已经证明了

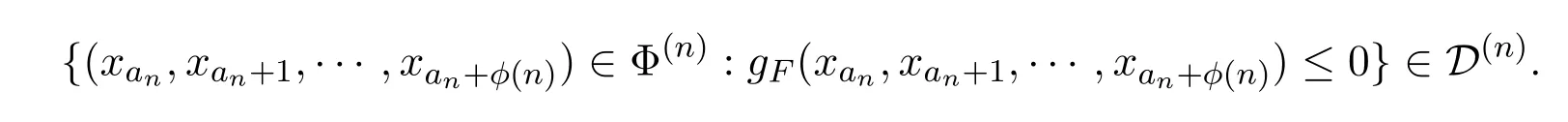
并且函数gF(xan,xan+1,···,xan+ϕ(n)) 是可测的,因此

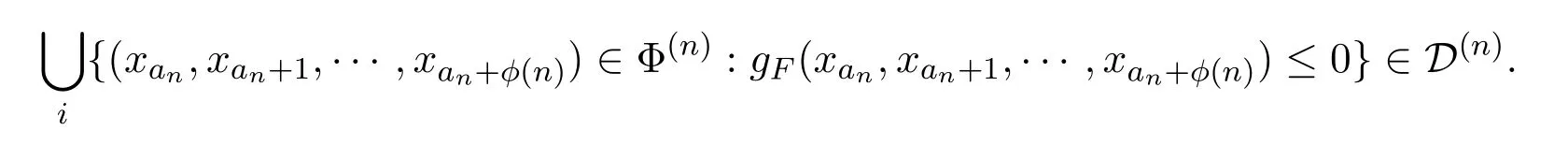
引理 3.2假设Xi≥0 a.s.,i=an,an+1,···,an+ϕ(n),并且

设

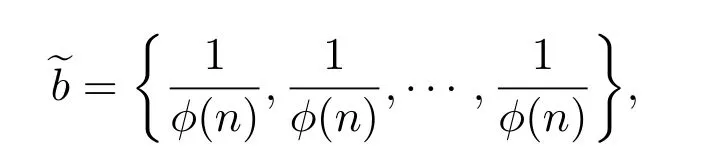
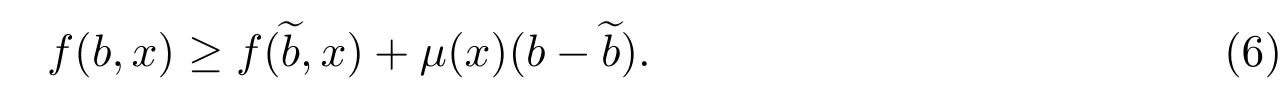
所有的b∈Rm,x∈Ω,并且 E‖µ(X)‖＜∞.

证明因为

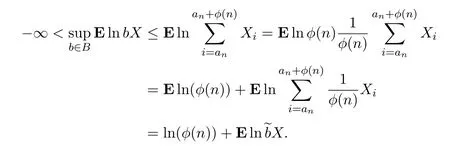
因此

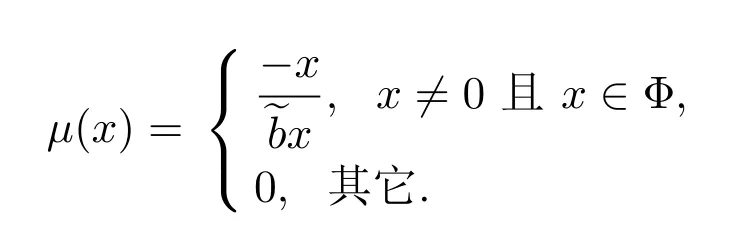
µ(x)显然是可测的.

若x=0或x∉Φ,那么∞≥∞+0.

若b∉B,x≠0且x∈Φ,那么

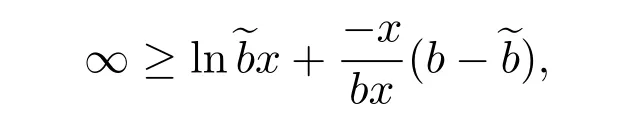
若b∈B,x≠0且x∈Φ,那么

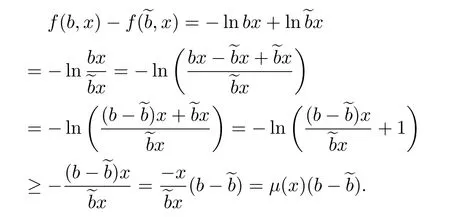
此外

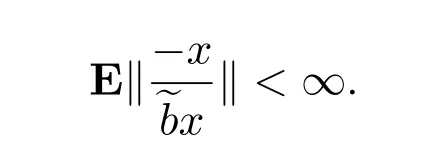
引理 3.3[8]设Y是概率空间(Γ,A,F)的随机变量,其中A表示包括关于F的σ-代数.

考虑下列假设:

假设 1g(·,·):Rk×Γ→R∪{∞}是一个凸的正被积函数,那么

(1)∀y ∈Γ,集合 epig(·,y)是闭的.

(2)y→epig(∩,y)的映射是可测的,且对闭子集

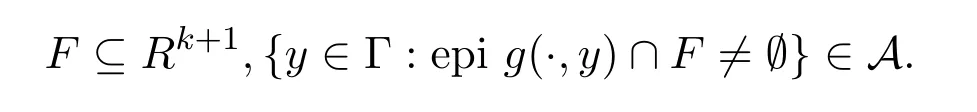
(3)∀y∈Γ,epig(·,y)几乎处处是凸的,且不是空集.

假设 2存在∈Rk,使得是有限的,且可测函数µ(·):Γ→Rk,使得

(1)对所有c∈Rk,y∈Γ,有

假设 3随机变量Yi是独立同分布的.

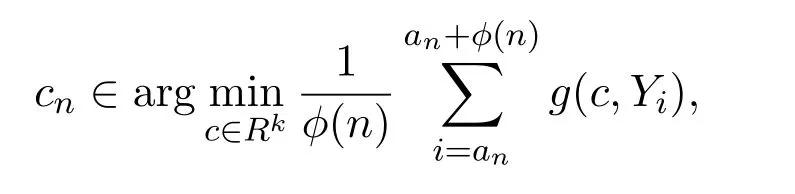
那么

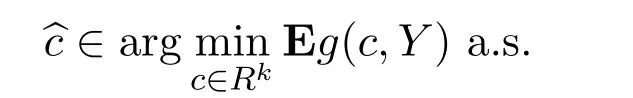
证明参见文献[8]的定理2.3和命题2.1,文献[9]的定理3.4.

引理 3.4假设随机股票市场收益率向量Xi是独立同分布的,且

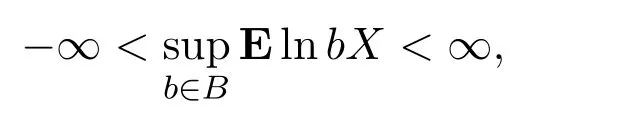
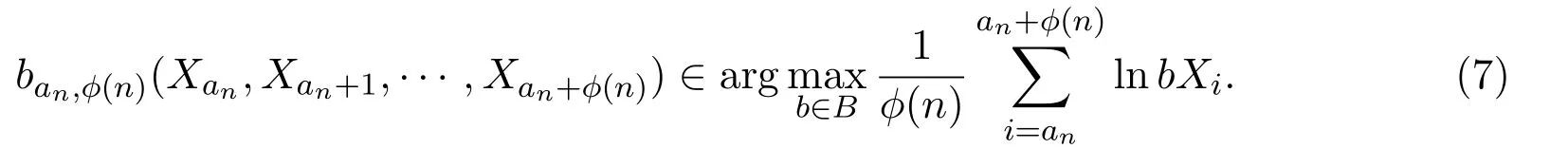
证明根据引理3.1,文献[10]定理1C和定理2K得到可测选择

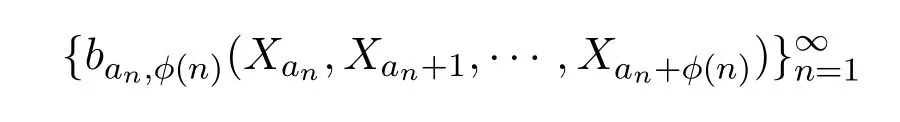
的存在性,那么

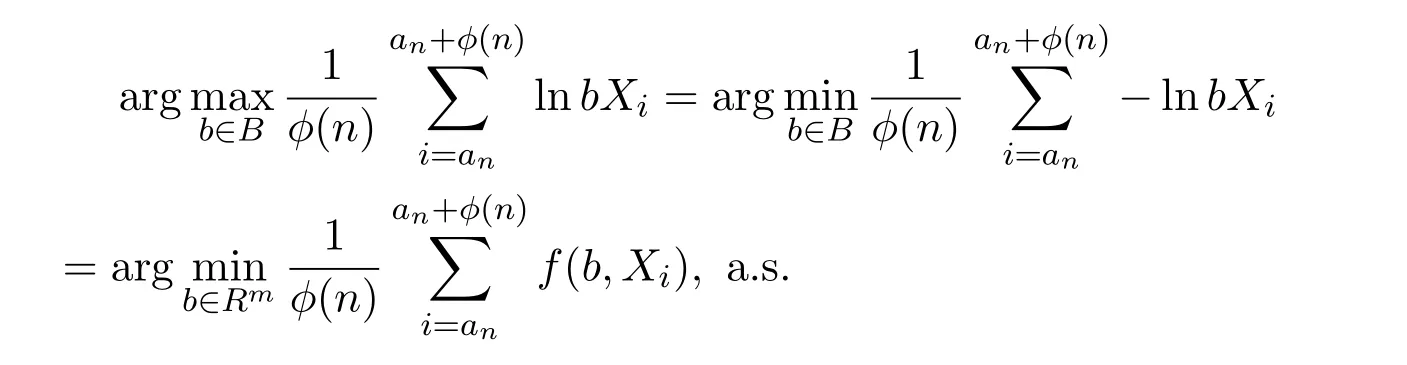
对所有b∈B,有

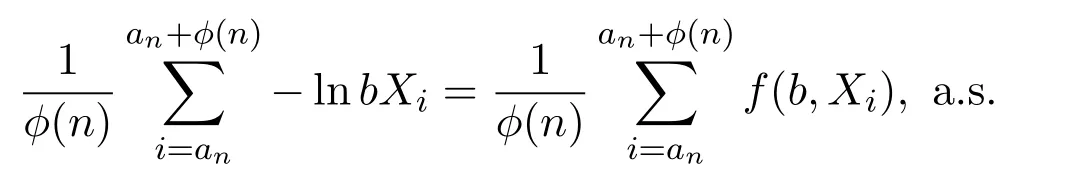
那么根据引理3.1,引理3.3得到聚点的对数最优.

引理 3.5经验对数最优投资组合的聚点和建立的投资组合选择一致,因此序列

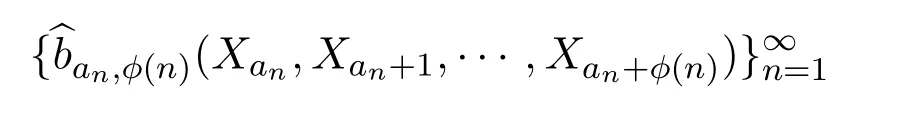
的聚点依概率1是对数最优.

证明设由于

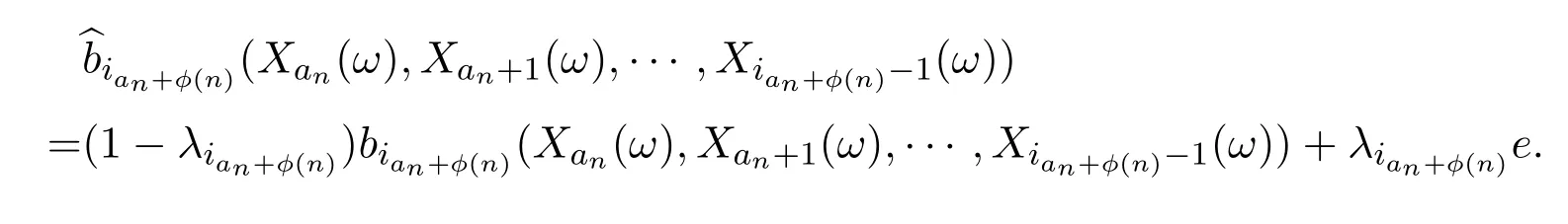
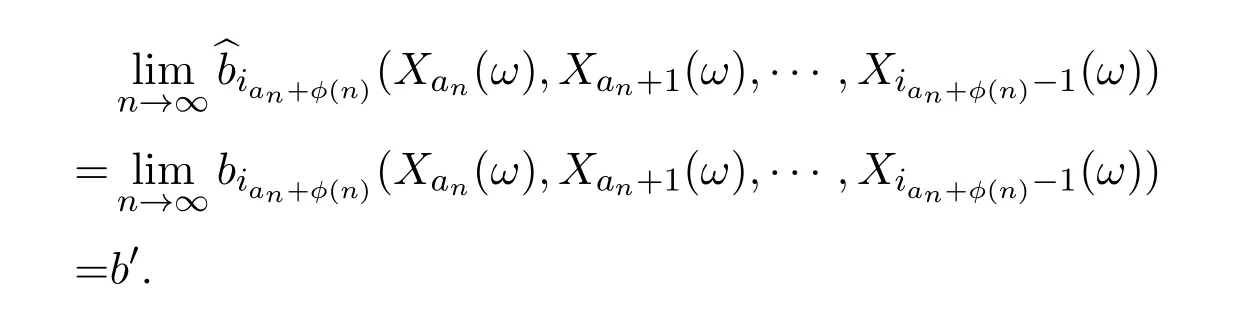
反之证明类似.

设

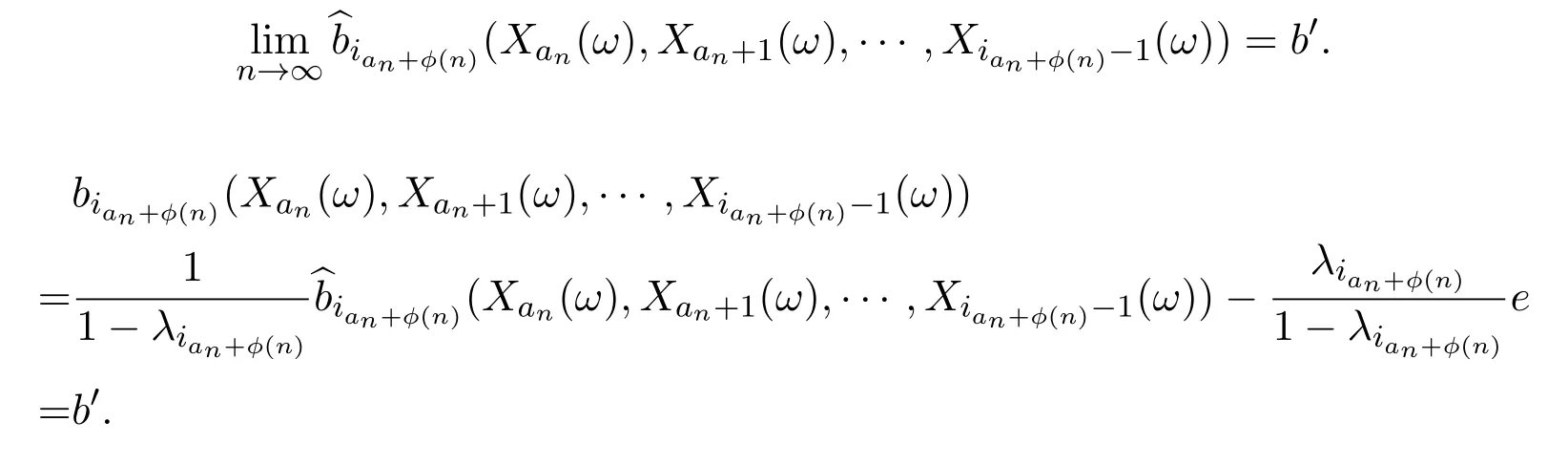
由引理3.4得对数最优性.

引理 3.6设随机股票市场收益率向量Xan,Xan+1,···,Xan+ϕ(n)是独立同分布的,且

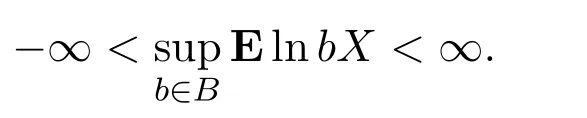
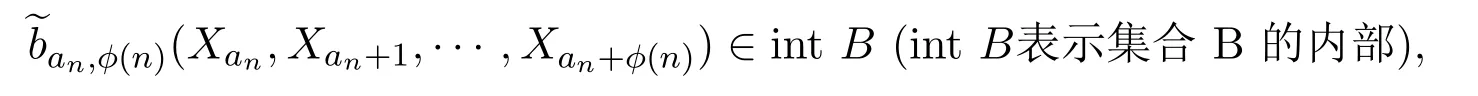
且

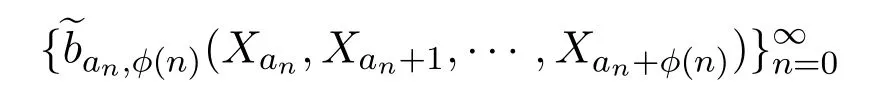
的聚点几乎处处是对数最优的,那么

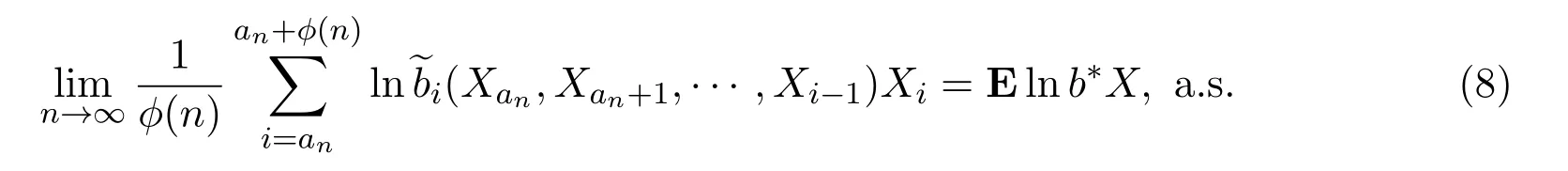
证明设b∗′是一个最优投资组合使得即对所有那么存在一个投资组合,假设且且包含的0的个数小于如果这个新的投资组合不满足条件,我们可以重复这个步骤.最多经过m步,可得到一个适合的投资组合.

存在集合L使得P(X∈L)=1且

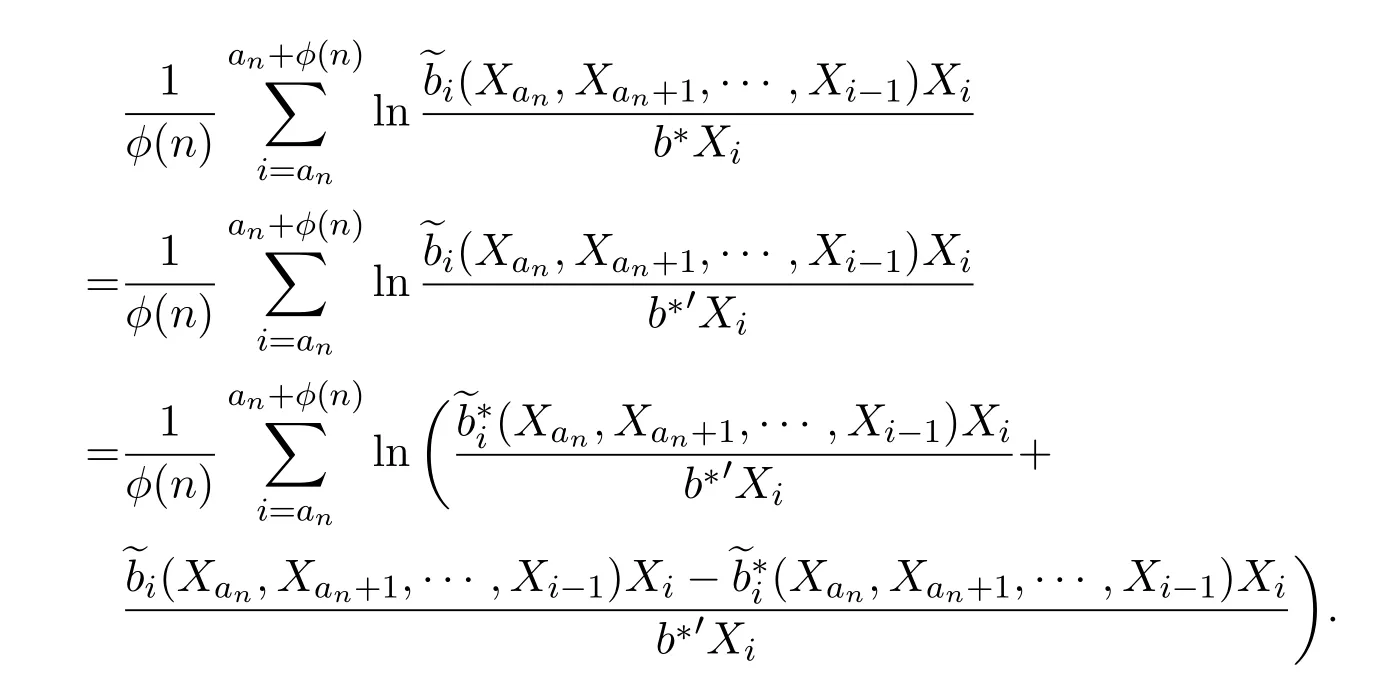
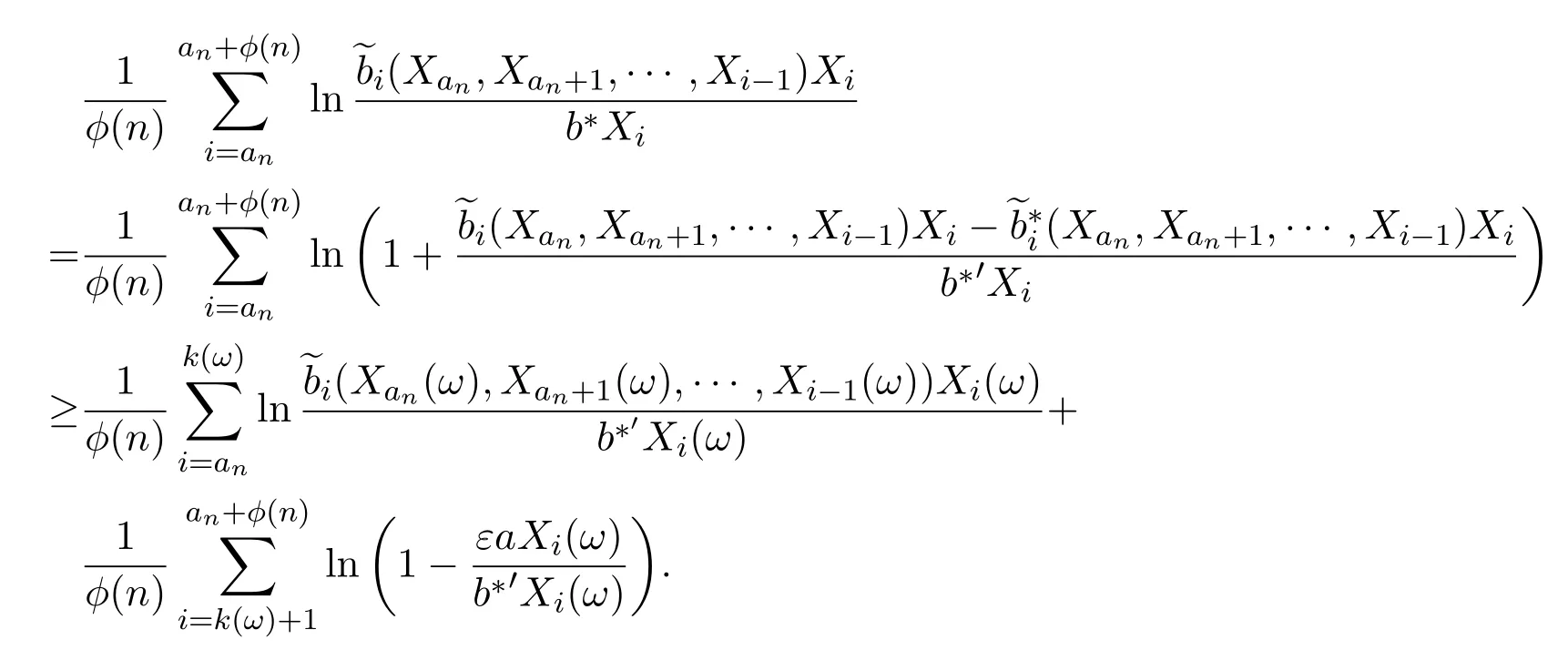
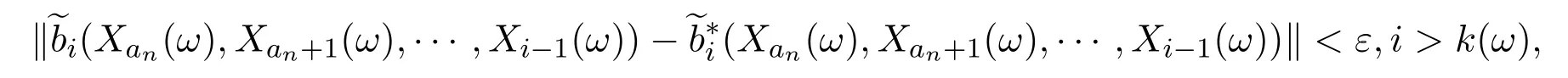
其中

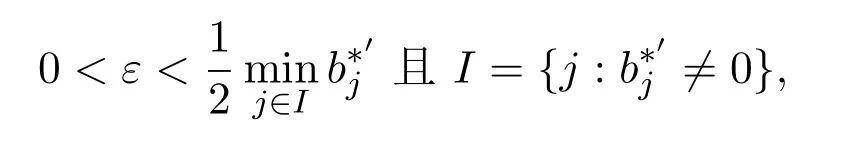
因此

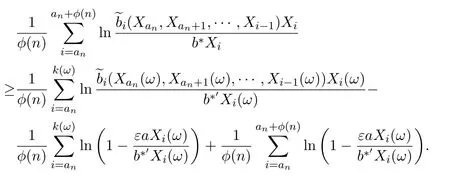
因此

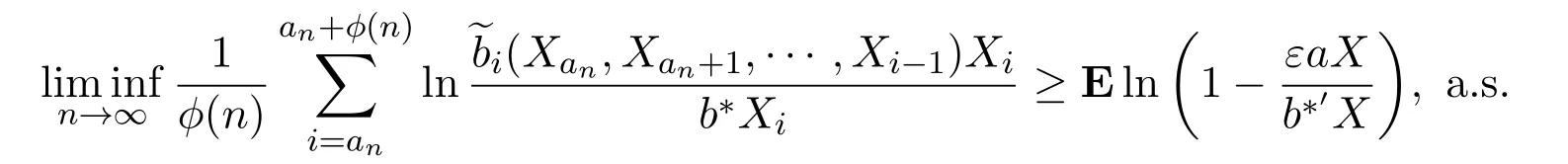
利用泰勒级数在区间[0,ε]中扩展函数令

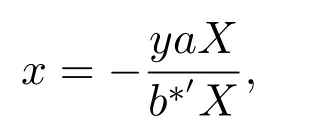
由麦克劳林公式,可得到

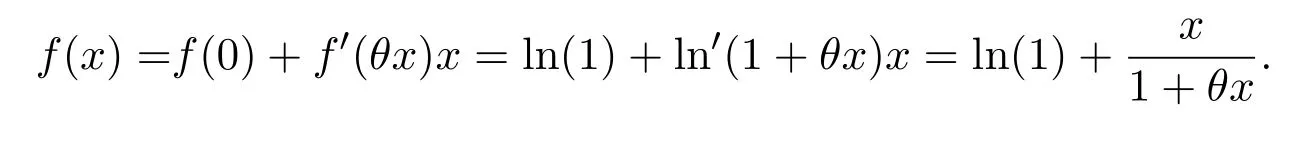
将

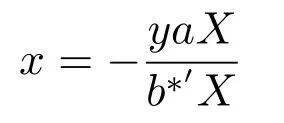
代入上式,有

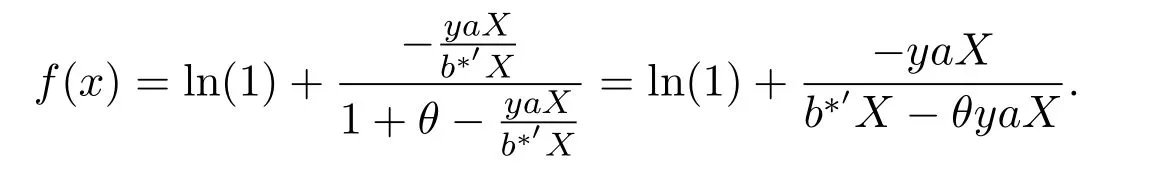
令t=θy,有

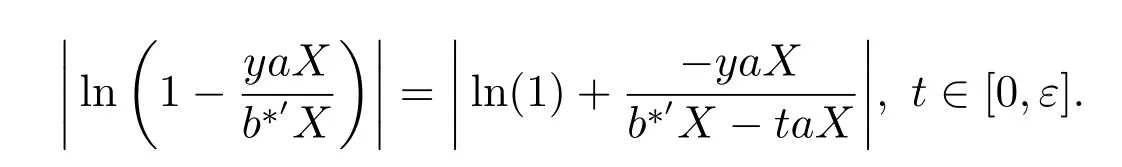
因此

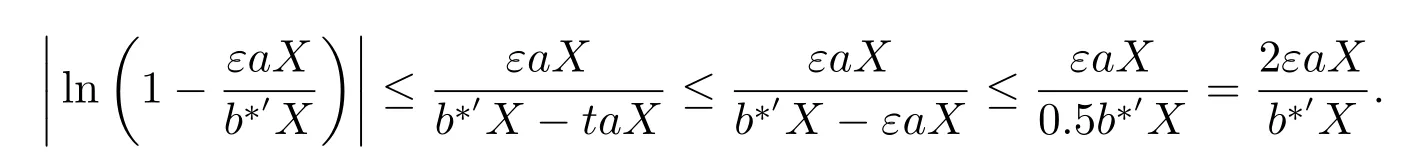
由对数最优性[11],

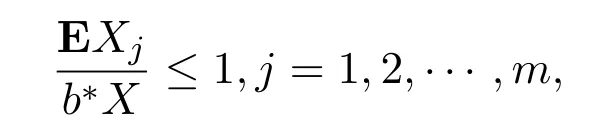
因此

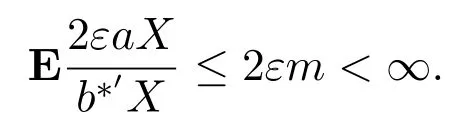
其中ε是任意的,

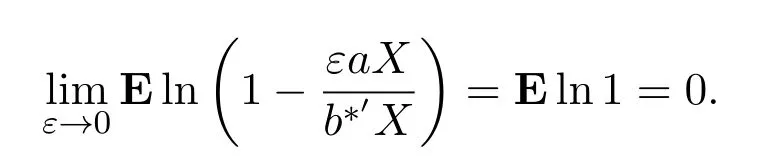
由勒贝格控制收敛定理,上界类似

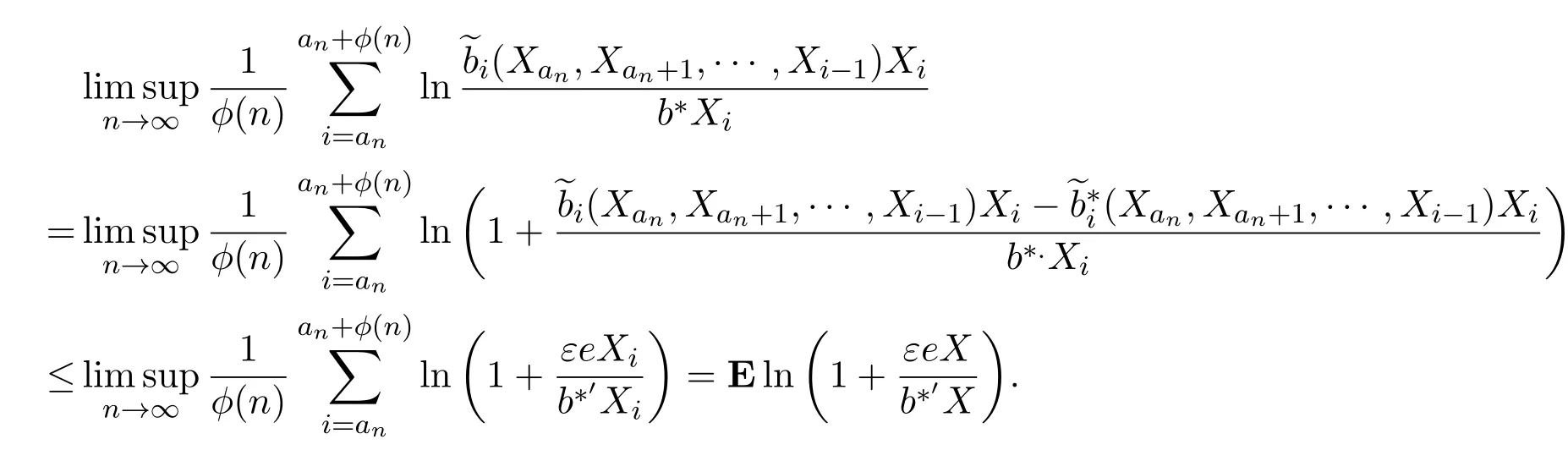
其中e=(1,1,···,1),ε是任意的

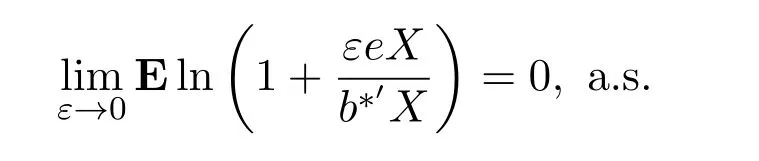
根据勒贝格控制收敛定理,因此

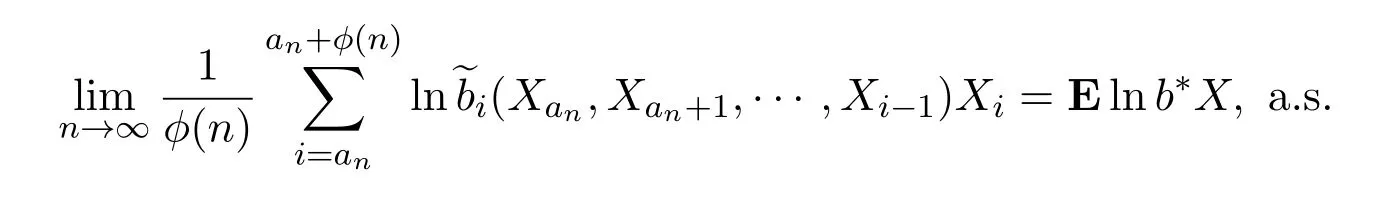
4 主要结论

定理 4.1假设Xan,Xan+1,···,Xan+ϕ(n)是独立同分布的随机股票市场收益率向量,并且

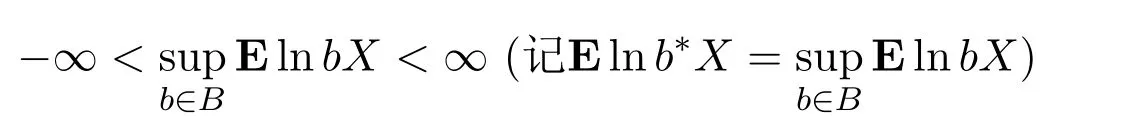
那么

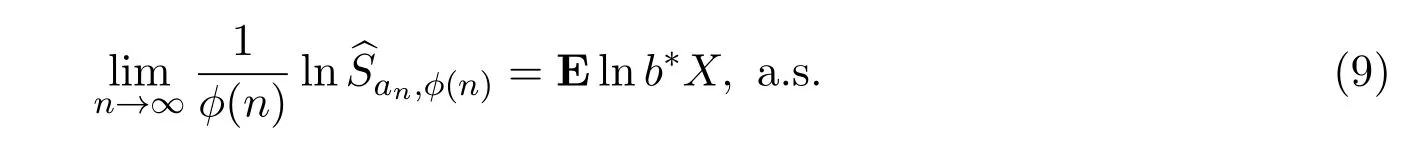
其中

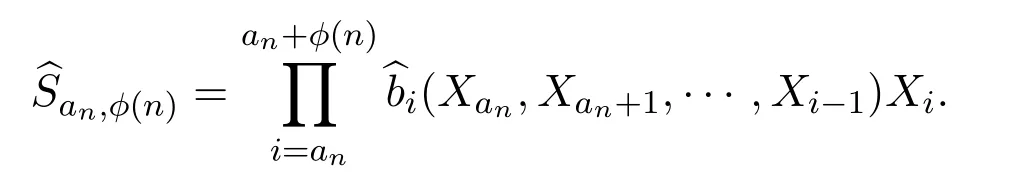
证明根据引理 3.5,的聚点是对数最优的.对所有n,有

因此定理4.1由引理3.6推断.

定理4.1解释了当随机股票市场收益率向量是独立同分布的,那么资本渐近最优增长率是根据所建立的投资组合选择实现的.在进一步优化了文献[6]中的模型后,所建立的模型相较于文献[6]中的应用范围更广,这一结果的证明确立了普通投资选择与滑动投资模型之间的密切联系.然而,值得注意的是,在实际生活中,经济人不能仅依赖纯理论的经验对数最优投资选择,因为它可能导致我们最终破产.

[1]Markowitz H.Portfolio Selection[J].Journal of finance,1952,7:77-91.

[2]姚海洋,易建新,马庆华.共同基金和无风险资产投资的最优策略[J].纯粹数学与应用数学,2006,22(2):154-158.

[3]张贺清.均值和方差变动的马科维茨投资组合模型研究[D].哈尔滨:哈尔滨工业大学,2015.

[4]李银兴,李彩萍.允许投资组合条件下概率准则[J].纯粹数学与应用数学,2003,19(2):185-190.

[5]邓雪.最小风险组合证券非负投资比例系数的确定[J].纯粹数学与应用数学,2007,23(4):524-528.

[6]Morvai Gusztáv.Portfolio choice based on the empirical distribution[J].Kybernetika,1992,6:484-493.

[7]Cover T M,Thomas J A.Elements of Information Theory[M].2nd ed.New York:John Willey Sons Inc,2006.

[8]King Alan J,Wets Roger J B.Epi-consistency of convex stochastic programs[J].Stochastics Rep.,1991,34:83-92.

[9]Wets Roger J B.Constrained estimation:consistency and asymptotics[J].Appl.Stochastic Models Data Anal.,1991,7:17-32.

[10]Rockafellar R T.Integral Functionals,Normal Integrands and Measurable Selections[M].In:Nonlinear Operators and the Calulus of Variations(Lecture Note in Mathematics).New York:Springer-Verlag,1976:157-207.

[11]Algoet A H,Cover T M.Asymptotic optimality and asymptotic equipartition properties of log-optimum investment[J].The Annals of Probability,1988,16(2):876-898.