由六个顶点的箭图诱导的项链李子代数

余德民, 梅超群

(1.湖南理工学院数学学院,湖南 岳阳 414006;2.首都经济贸易大学统计学院,北京 100070)

1 引言

Z为整数集合,C为复数域,项链李代数是新的一类特征0上的无限维李代数.在非交换几何的研究中,当探讨Weyl代数A1(C的C-代数自同构群AutA1(C)在轨道Weyln上的作用时,得到一个AutA1(C)在n×n矩阵轨道空间Calon上的可迁作用,但是此作用是不可微的,从而是非代数的.Berest和Wilson提出是否可将Calon等同于某种无限维李代数的余伴随轨道.文献[1-2]都曾用项链字刻画自由李代数的基,来试图解决Berest和Wilson提出的问题,但都没有成功,文献[3-4]分别引入了项链李代数解决了这一问题.项链李代数是某一箭图Q所诱导的重箭图¯Q中全体项链字为基张成的无限维向量空间,并在此向量空间上定义了特殊的李运算.箭图在代数表示论应用已经越来越广泛[5-6],并成为代数表示论的基本概念.项链李代数在非交换几何及奇点理论,量子群等领域有着重要的应用.我们曾经研究过一些项链李代数的同构和同态[7-8],在文献[7]中研究了一些特殊箭图的同构,这些同构包括单向循环箭图,混向循环箭图以及垂直叠加的箭图和水平叠加的箭图的同构.在文献[8]中研究了些特殊箭图的同态,这些同态包括只有两个顶点,两条不同方向的箭图,只有三个顶点,三条同方向的箭图以及n个顶点,n条不同方向的箭图的同态.梅超群[9]研究了项链李代数的一些特殊项链李代数的结构.文献[10]研究了可传递李代数的结构.本文重点讨论了由一个特殊箭图诱导的项链李子代数,并证明了其中一些李子代数是半单李代数.后续研究工作将探讨项链李代数的一些重要性质,如半单性,可解性,可分解性.

2 主要结果

令

是任一具有两个或两个以上顶点的连通有向图,其中

是Q的顶点集合,Q中的有向边称之为箭,

Q1是Q中所有箭的集合,s,t是从Q1到Q0的映射,使对∀α∈Q1,s(α)=v是α的起点,t(α)=v′是α的终点,记作α:v→v′,且s(α)≠t(α),并称Q是一个箭图.Q中有箭序列:

这里i1,···,iu ∈ {1,···,m}.如果满足

则称

为Q中的路,若还有则称c是一个循环,u称为循环的长度.在箭图Q的所有循环集合上定义关系～如下,设c是Q中的一个循环,若c′是依次轮换c中的箭头而得到的循环,定义c′～c.显然～是等价关系.Q的一个循环等价类称为Q的一个项链词.若是循环,则相应的项链字用图 1表示如下:

图1 循环c=···对应的项链字

对于Q中的每个箭α:v→ v′,添加α关于v,v′的对称箭α∗,即α∗:v′→ v,α∗称为α的星化得到Q所诱导的重箭图.记

β∗也称为β的星化。显然从定义可知将中所有的循环等价类即所有的项链词构成集合记此集合中所有的元素为基在C上张成向量空间为NQ.

(ω1,ω2的箭的下标排列顺序一旦取定之后,便再不能置换),∀i ∈ {1,···,r},j ∈ {1,···,s},∀α ∈Q1,在集合定义二元运算如下[3-4]:

将上述李运算线性地扩展到NQ,对于任意的ai,bj∈C,x,y∈NQ,令

定义

可验证上述定义的李运算[ω1,ω2]与ω1,ω2所选的循环代表无关,及箭的排列顺序无关.

根据(1)式与如下图2所示的项链字,可以形象的定义李运算:对有

图2 李运算的形象定义

即∀α ∈Q1,如果α出现于ω1中,再找寻α∗是否出现于ω2中,若是,则同时删去α和α∗,以打开ω1和ω2这两个项链,将打开后的两条路的首尾对应相接（同一顶点接在一起）,构成一个新的项链字,若α在ω1出现n1次,若α在ω2出现n2次,则这个过程需重复n1n2次,这n1n2个项链字的和构成一个新的项链字的组合,若α∗不在ω2中,则将新的项链字看作0.然后在ω2中找寻上述的α,在ω1中找寻α∗.重复上述操作,得到又一新的项链字组合,用先得到的新的项链字组合减去后得到项链字组合,最后遍历∀α∈Q1,把相减后得到的所有的项链字加起来,和式为 [ω1,ω2].因为

所以

于是此李运算在此向量空间NQ上满足反对称性,也可验证此李运算满足双线性和封闭性和Jacobi恒等式.

假定六个顶点的箭图如图3所示:

图3 箭图

如果一个项链字

那么k1,k2称为项链字ω1的复制指数.

如果一个项链字

那么k1,k2称为项链字ω1的复制指数.

g1是α2α∗2(α2α3α1)k1(α4α5α6)k2,∀k1＞0,∀k2＞0,k1,k2∈Z,张成的线性空间;

g2是α4α∗4(α2α3α1)q1(α4α5α6)q2,∀q1＞0,∀q2＞0,q1,q2∈Z,张成的线性空间;由于∀k1＞0,k1∈Z,k2＞0,k2∈Z,q1＞0,q1∈Z,q2＞0,q2∈Z,

从而g1是李子代数.

∀k1＞0,k1∈Z,k2＞0,k2∈Z,令为则有

由于∀k1＞0,k1∈Z,k2＞0,k2∈Z,q1＞0,q1∈Z,q2＞0,q2∈Z,

从而g2是李子代数.

∀k1＞0,k1∈Z,k2＞0,k2∈Z,令为则有

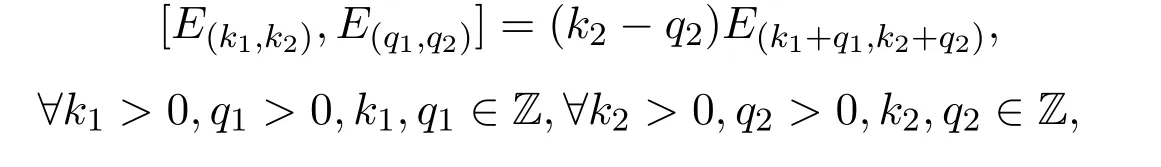
由于∀k1＞0,q1＞0,k1,q1∈Z,k2＞0,q2＞0,k2,q2∈Z,g是

张成的线性空间.∀k1＞0,q1＞0,k1,q1∈Z,k2＞0,q2＞0,k2,q2∈Z,

即∀k1＞0,q1＞0,k1,q1∈Z,k2＞0,q2＞0,k2,q2∈Z,

从而g是李子代数.本文重点研究李子代数g1及g2的李子代数的性质.

命题 2.1

证明建立g1到g2的线性映射如下:

从而原命题成立.

命题 2.2g2的中心为:

证明设

因为x∈c(g2),∀y∈g2有 [x,y]=0,取

因为c1,c2为任意整数,取

则

另外，该项目主体结构为双塔结构，两侧双塔区域为混凝土剪力墙，双塔之间地下室区域为框架结构，其整体性及刚度存在较大差异，水化热的释放选择在薄弱区域，因此地下室顶板裂缝主要出现在双塔之间的—/○A—○G区域；并且由于东西向长为55.13 m，而南北向仅长28.20 m，地下室顶板类似于单向板受力状态，其不利受力位置为东西向跨中，这也就能解释为什么地下室顶板裂缝主要沿南北方向分布.

构造上的g1到的线性映射如下:

f1在g1的基向量

线性扩张.

命题 2.3f1是李代数g1到的同态，且Kerf1是g1的无限维非交换真理想.

证明从f1的构造知f1是g1到的线性映射,可验证:

从而

因为

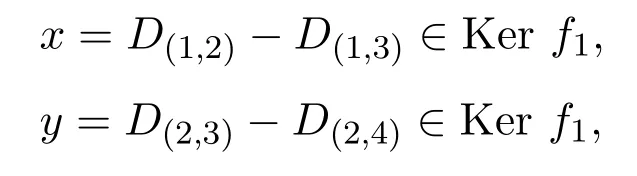
为Kerf1的线性无关的向量,随着n无限增大,Kerf1为无限维线性空间.因为D(1,2)∈g1,而f1(D(1,2))≠0,从而Kerf1为无限维非交换真理想.

命题 2.4设

[u1,u2]=0当且仅当c1=c2.

证明当c1=c2时,显然[u1,u2]=0.

充分性:不妨设

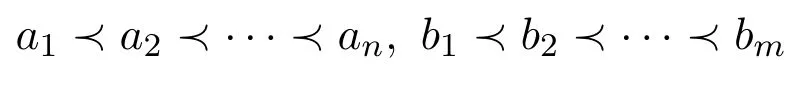
否则只需调整一下次序.因为

所以

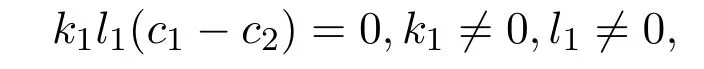
从而

构造g上的自同构映射如下:

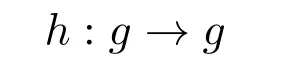
h在g的基向量上线性扩张.

命题 2.5h是李代数g的自同构,且将h限制在g1上,则h是g1到g2的同构.将h限制在g2上,则h是g2到g1的同构.

证明从构造知h为g上的线性映射,经计算可验证:

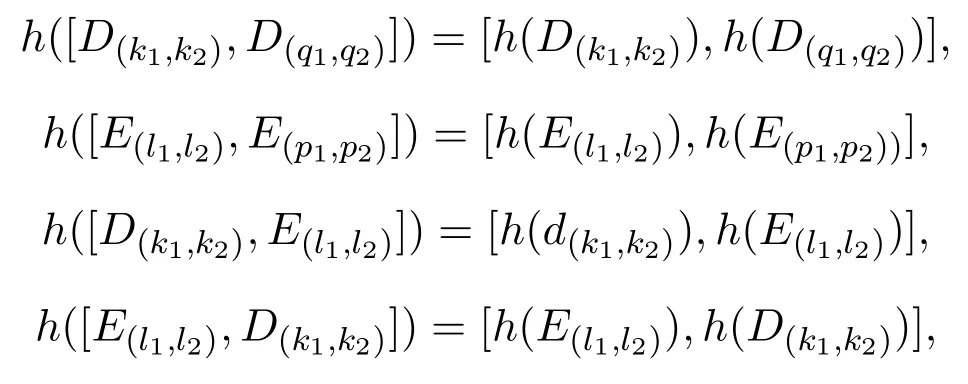
从而

将h限制在g1上,则h是g1到g2的同构,将h限制在g2上,则h是g2到g1的同构.

[1]Lothaire M.Combinations on Words[M].London:Cambridge University Press,1983.

[2]Reutenauer C.Free Lie Algebras[M].Oxford:Clarendon Press,1993.

[3]Bocklant R,Le Bruyn L.Necklace lie algebras and nocommunicative symplectic geometry[J].Math.Z.,2002,240(1):141-167.

[4]Ginzburg V.Non-commutative symplectic geometry,quiver varieties and operads[J].Math.Res.Lett.,2001,8(3):337-400.

[5]Guo J Y,Martinez-Villa R.Algebra pairs associated to mckay quivers[J].Comm.Algebras,2002,30(2):1017-1032.

[6]Peng L G.Lie algebras determined by finite auslander reiten quivers[J].Comm.Algebras,1998(1):235-258.

[7]Yu D M,Guo J Y,Mei C Q.Automorphisms and automorphism groups of necklace lie algebra[J].Chinese Annals of Mathematics(in Chinese),2012,34(5):569-578.

[8]Yu D M,Guo J Y,Mei C Q.Homomorphisms of some special necklace lie algebra[J].Chinese Annals of Mathematics(in Chinese),2009,30(4):551-562.

[9]Mei C Q,Yu D M.The structure of necklace lie algebras[J],Journal of Mathematics in Practice and Theory,2012,42(1):195-204.

[10]Post G.On the structure of transitively differential algebras[J].J.Lie theory,2001,11:111-128.