教材中一道立体几何问题的多视角探究

☉浙江省宁波市第二中学 李建明

教材是我们日常学习的主要载体，教材中的例题、习题具有典型性和代表性，对其进行多方法求解、多角度探究，是巩固所学知识的重要途径，本文以北师大版必修2中的一道立体几何习题为例说明，以期抛砖引玉.

题目 （北师大版必修2例题）如图1所示，已知正方体ABCD-A1B1C1D1，求证：平面AB1D1∥平面C1BD.

本题的证明较为简单，利用线线平行即可证明面面平行.分析近年模拟题及高考题，以此题为背景的试题屡见不鲜，下面简举几例.

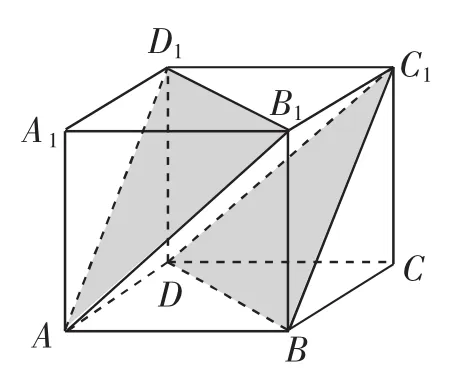
图1

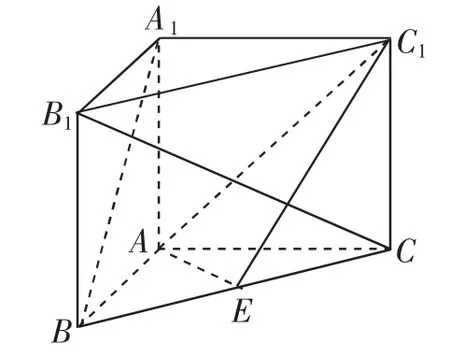
图2

一、变换几何体的类型

例1（2017年北京高考模拟）如图2所示，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1，且E是BC的中点.

（1）求证：A1B//平面AEC1；

（2）求证：B1C⊥平面AEC1.

分析：不难看出将题目中的几何体沿对角面A1C1CA一分为二，即可得本题中的几何体，本题证明线面可行，通常可从如下两个视角入手.

解：（1）证法1：如图3所示，取B1C1的中点M，连接BM.因为MC1∥BE，且，所以四边形MC1EB为平行四边形，所以BM∥EC1.

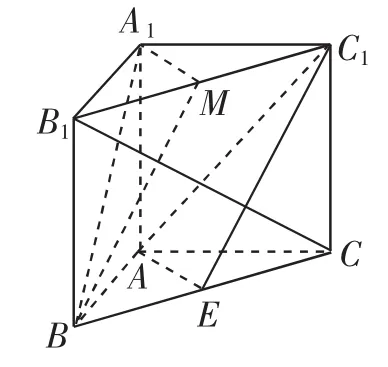
图3

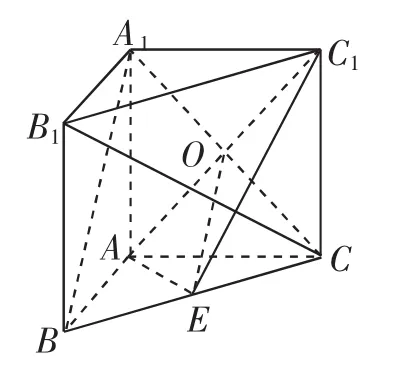
图4

又A1M∥AE，A1M∩BM=M，C1E∩AE=E，所以平面A1BM∥平面AEC1，所以A1B∥平面AEC1.

证法2：如图4所示，连接A1C，交AC1于点O，连接OE，因为四边形AA1C1C为矩形，所以O为A1C的中点.

因为E为BC的中点，所以OE为△A1BC的中位线，所以OE∥A1B.又因为OE⊂平面C1AE，A1B⊄平面C1AE，所以A1B∥平面AEC1.

（2）略.

评注：证明线面平行通常有两种视角：（1）在面内寻找一条与已知直线平行的直线，由线面平行的判定可证.证法1即为此视角.（2）构造已知直线所在的平面，证明两平面平行.利用面面平行的性质证明.证法2即为此视角.

二、变换问题条件

例2 如图5所示，在三棱柱ABC-A1B1C1中，AA1⊥底面ABC，∠BAC=90°，AB=AC=2，AA1=.M、N分别是BC和CC1的中点，P为侧棱BB1上的动点.

（1）求证：平面APM⊥平面BB1C1C；

（2）假设P为线段BB1的中点，求证：A1N∥平面APM.

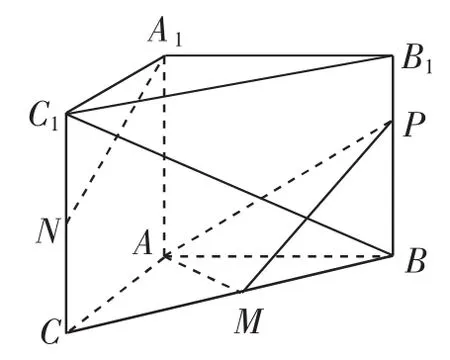
图5

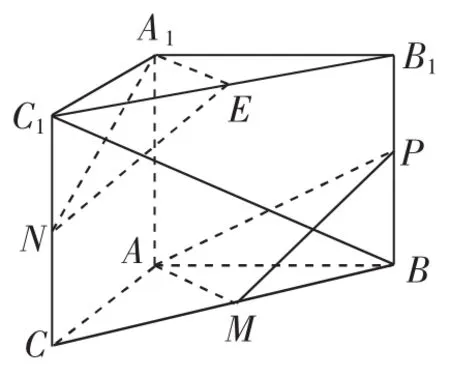
图6

解析：（1）略.

（2）证法1：如图6所示，取B1C1的中点E，连接A1E，NE.由已知条件易证A1E∥AM，NE∥PM，且A1E∩NE=E，PM∩AM=M，所以平面A1EN∥平面

PAM.又因为A1N⊂平面PAM，所以A1N∥平面A1NE.

证法2：如图7所示，取AA1

的中点S，连接SC、SB，SB交PA 于点T，连接MT.

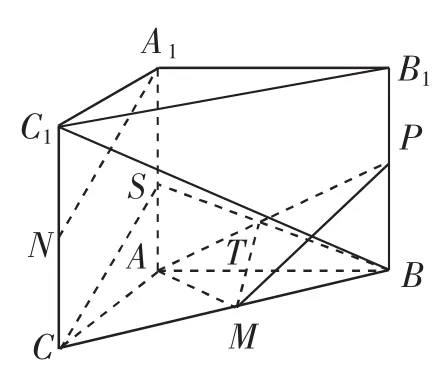
图7

易知四边形SABP为平行四边形，所以T为SB的中点，所以MT为△SBC的中位线，所以MT∥SC，又因为A1N∥SC，所以MT∥A1N，所以A1N∥平面APM.

评注：证法1是从面面平行的角度入手，即构造经过A1N且与平面APM平行的平面.证法2是从寻找线线平行的角度入手，即通过构造三角形的中位线，在平面SBC内找到与A1N平行的直线，从而实现了问题的证明.

三、变换问题结论

例3 如图8所示，在正方体ABCD-A1B1C1D1中，E是棱DD1的中点，P是侧面CDD1C1上的动点，且B1P//面A1BE，则B1P与平面CDD1C1所成角的正切值构成的集合是（ ）.

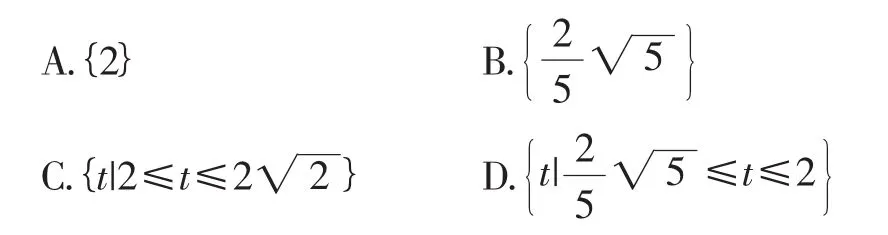
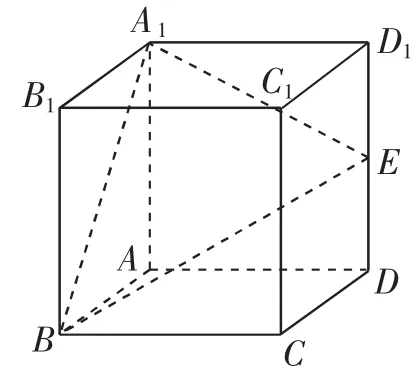
图8

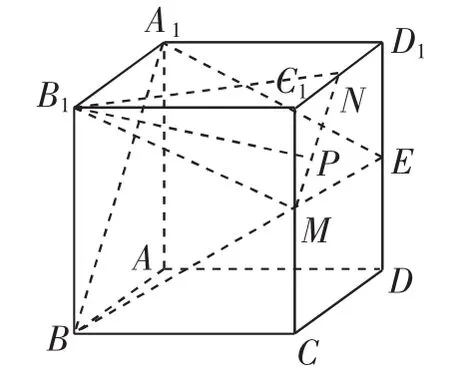
图9

解析：如图9所示，取CC1的中点M，C1D1的中点N，连接B1M，B1N，MN.

易知B1M∥A1E，MN∥A1B，所以平面B1MN∥平面A1BE，已知B1P//面A1BE，故点P在线段MN上.

因为B1C1⊥平面C1D1DC，所以B1C1⊥C1P，所以∠B1PC1即为B1P与平面CDD1C1所成的角.在△B1PC1中，tan∠B1PC1=，故当点P与点M或N重合时，tan∠BPC取得最小值112，当点P是MN的中点时，tan∠B1PC1取得最大值

故正确选项为C.

评注：P是平面CDD1C1上的动点，但B1P平行于平面A1BE，所以B1P在一个与平面A1BE平行的平面内，因此转换求解视角去寻找与平面A1BE平行的平面.

四、变换问题背景

例4 （2016年全国卷Ⅰ）已知平面α经过正方体ABCD-A1B1C1D1的顶点A，平面α//平面CB1D1，平面α∩平面A1B1C1D1=m，平面α∩平面ABB1A1=n，则直线m，n所成角的正弦值为（ ）.

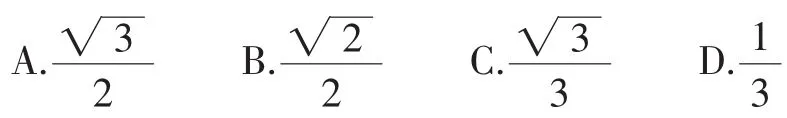
解法1：如图10所示，延长D1A1至点D2，使得A1D2=D1A1.延长B1A1至点B2，使得A1B2=B1A1.连接B2D1，B2D2，AB2，AD2，B1D2.

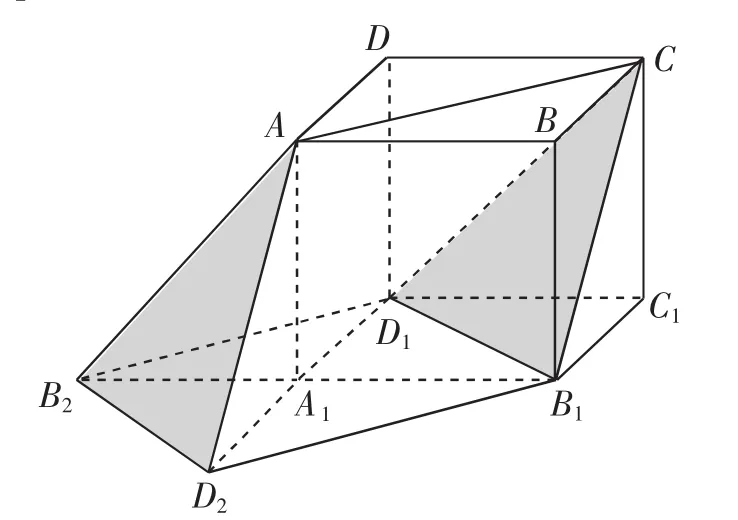
图10

易知B2D2∥B1D1且B2D2=B1D1，AB2∥CD1且AB2=CD1，AD2∥CB1且AD2=CB1，所以平面AB2D2∥平面B1CD1，所以平面AB2D2即为题目中的平面α，B2D2即为直线m，AB2即为直线n.

又因为CD1，CB1，B1D1均为正方体ABCD-A1B1C1D1的面对角线，所以CD1=CB1=B1D1，所以B2D2=AB2=AD2，即△AB2D2为正三角形，则直线m，n所成角即为AB2与B2D2的夹角，其大小为，故直线m，n所成角的正弦值为

解法2：如图11所示，构造与正方体ABCD-A1B1C1D1相连的正方体，则已知条件中的各种关系直观地体现出来.

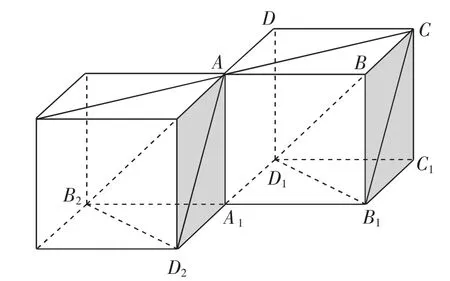
图11

易知平面AB2D2即为已知条件中的α，则直线m即为B2D2，直线n即为AB2.

评注：已知条件中平面α的位置并没有明确给出，直线m，n的位置亦不确定.因此构造出过顶点A且与平面CB1D1平行的平面α，这是问题求解的关键.

综上所述，通过对课本例题、习题作必要的挖掘、探究、引申，有助于学生构建知识网络，进而对数学问题的类型及解决问题的方法有一个明确的认识.对例题进行挖掘，是引导学生跳出题海，减轻负担的重要举措.F