巧构知识导图 妙用一题多解

☉河南省内乡县高级中学 齐若贝

一首优美的经典音乐，不论哪个歌手翻唱，抑或用不同的乐器演奏，都是旋律优美，百听不厌.平时我们有做不完的题，而每道题有可千变万化，我们在解一些好题、难题时，往往百思不得其解，丝乱如麻，正所谓“东风夜放花千树，更吹落，星如雨”，但如果学会用策略导图，进行不同事物之间转换，从不同角度进行不同的解法，然后从中寻求最简捷的方法，以待考试用，厚积而薄发，问题自然迎刃而解，正所谓“众里寻他千百度，蓦然回首，那人却在，灯火阑珊处”.如此怎不让人叹为观止，拍案叫绝，回味无穷.

下面以一道填空题为例，谈谈用多元思维求解的策略方法.

一、问题

已知x，y都是大于0实数，若x2-xy+y2=1，求x+2y的取值范围是__________.

分析：这道题虽是填空题，还是有一定困难的.看似简单，似曾相识，思来想去，求不出正确答案.这样的题，一定要先分析，厘清思路后再动手.

二、绘制核心知识导图

利用核心知识导图的构建，通观了概念间的立体联系，形象快速地把握知识点间的关联，在分析和解决难题时思路非常清晰，让解题思路看得见，解题方法更快捷.本题主要采取6种方法，概括8个方面知识点，体现3种数学思想.

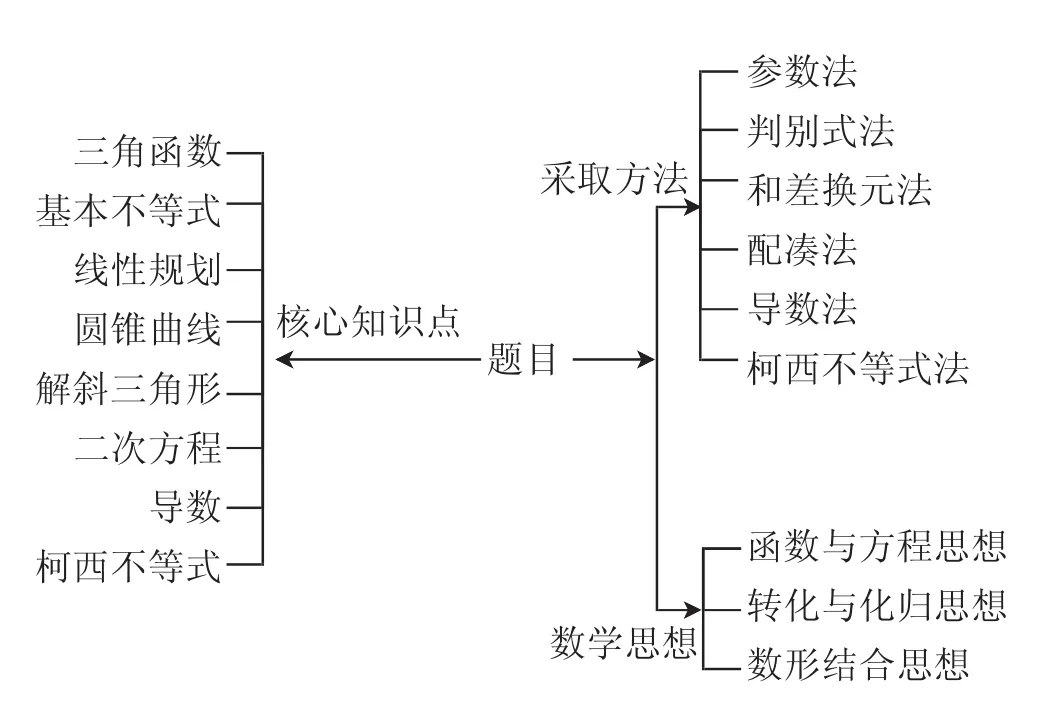
三、解法

（一）方法1：参数方程法

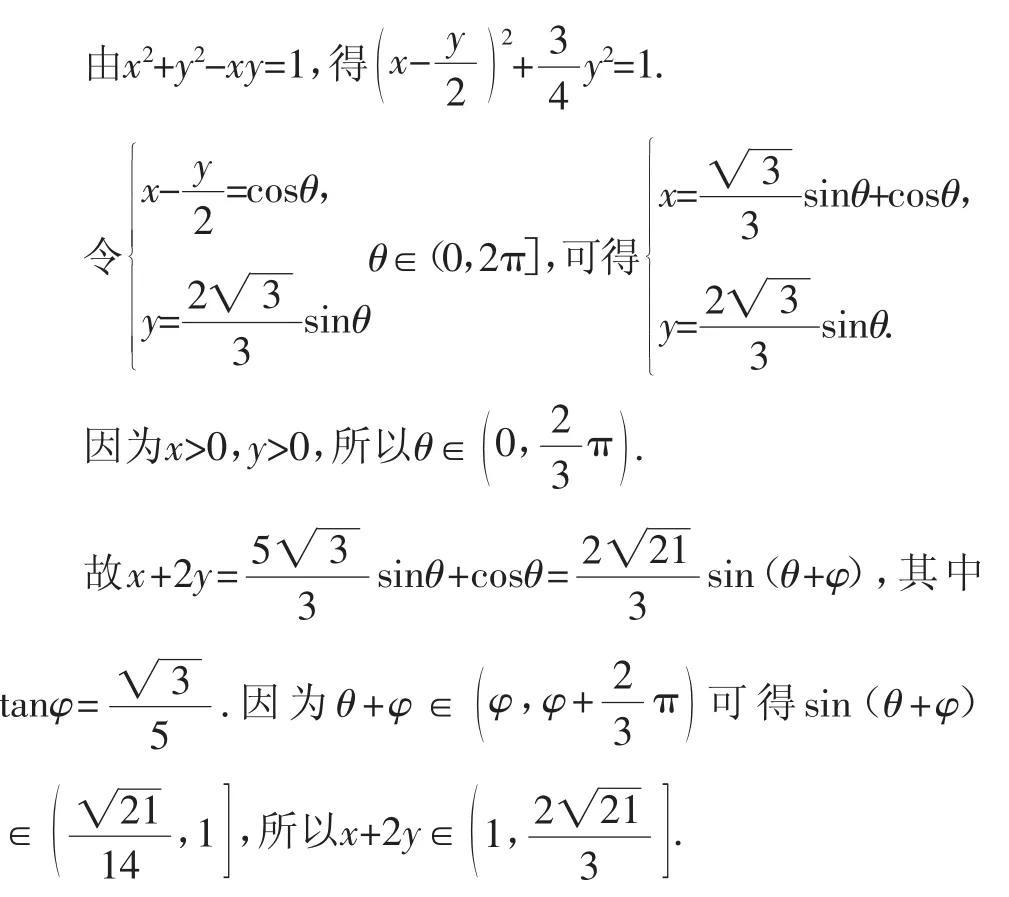
感悟：本法从圆的方程形式“x2+y2=1”受到启发，下面就是想办法怎样去掉条件式“x2+y2-xy=1”中的“xy”就好了，然后利用三角函数参数方程进行换元即可，此法比较大众化，是最易想到的方法.

（二）方法2：判别式法

设x+2y=t，则x=t-2y，代入x2+y2-xy=1，整理后得7y2-5ty+t2-1=0，则判别式Δ=-3t2+28≥0，由已知条件可得t＞0，解得

又因为y＞0，在函数f（y）=7y2-5ty+t2-1中，根据二次函数性质，所以f（0）＞0，解得t＞1.

感悟：此法巧妙转化方程有解问题，是最基本的一种方法，也是最常用、最易想到的方法.

（三）方法3：和差换元法

令x=m+n，y=m-n，代入x2+y2-xy=1，整理后得m2+3n2=1，又因为x=m+n＞0，y=m-n＞0，则m2+3n2=1表示椭圆的一部分，即直线m+n=0的上方，直线m-n=0的下方.

感悟：此法多用于数学竞赛中，妙在这种变换能改变问题的结构形式，使解题思路清晰，灵活新颖，步骤简洁，让人大开眼界.

（四）方法4：斜三角联想法

由已知条件知，可将x，y分别看成△ABC的两边a，b，则c=1，由x2+y2-xy=1，得a2+b2-ab=c2.

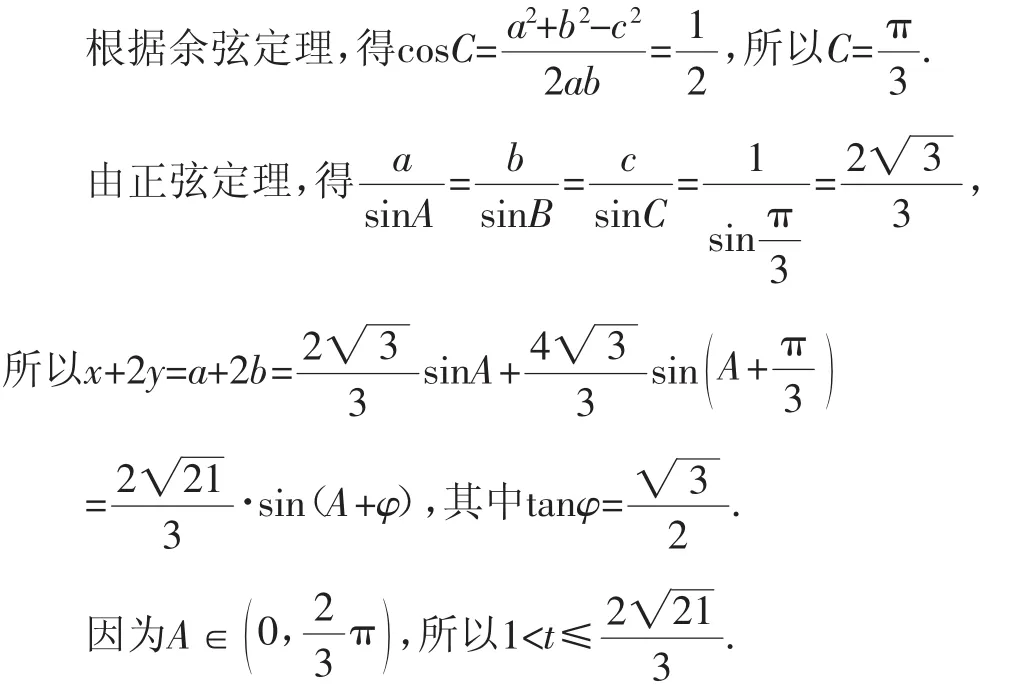
感悟：本法根据结构特征，巧妙联想到斜三角形函数形式，考查知识点多，既有三角函数变换、单调性，又有两角和差公式、正余弦定理，必须具备一定的推理能力、计算能力及联想能力.

（五）方法5：不等式配凑法

由x2+y2-xy=1，得xy=x2+y2-1.

设x+2y=t，则t2=x2+4y2+4xy，整理后可得t2=5x2+8y2-4.

感悟：有些题实在“看不出来”的情况下，把不等式变形，然后利用两次平方，待定系数法进行拼凑.此题内涵丰富，简约不简单.

（六）方法6：导数法

感悟：此法出现分类讨论，也涉及函数的单调性问题，一定要注意函数的定义域，是分段函数的要分开计算.但知识新颖，方法灵活，不失为一种方法.

（七）方法7：柯西不等式法

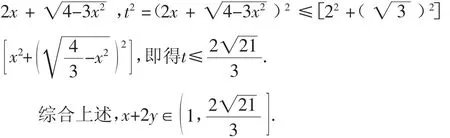
感悟：本题解法与导数法的前半部分一样，求t=x+2y=2x+的最值时用到柯西不等式.挖掘出题目隐含的条件，合理转化，巧妙拼凑出柯西不等式的结构形式，是解题的关键和亮点.

至此，我们已把问题研究得清晰透彻，也使脑洞大开.很明显，三角函数换元、判别式应用、图形结合是我们比较常用的方法，其他方法也很有学问，很耐人寻味，在平时练习的过程中，应不满足于一种解法，多思则多解，遇到具体问题才能做到随机应变，达到快速求解的目的.博观约取，厚积薄发，这是一个持久渐进的过程，贵在持之以恒.正所谓纵横广博，积累深厚，方能有所摘