极化恒等式的应用

☉郑州外国语学校 姚思宇

向量是沟通代数与几何的桥梁，向量的坐标运算为几何运算插上了“代数的翅膀”，从而实现了向量与几何、代数的巧妙结合.a·b=|a||b|cosθ建立了向量的数量积与两个向量的长度及其夹角之间的关系，极化恒等式a·b=却建立了向量的数量积与几何长度之间的关系.因此对研究向量的数量积有广泛应用.

一、极化恒等式

人教版必修4第二章第五节第一课时“平面几何中的向量方法”的例1中，证明了平面几何中一个常见的结论“平行四边形两条对角线的平方和等于两条邻边平方和的两倍”.

图1

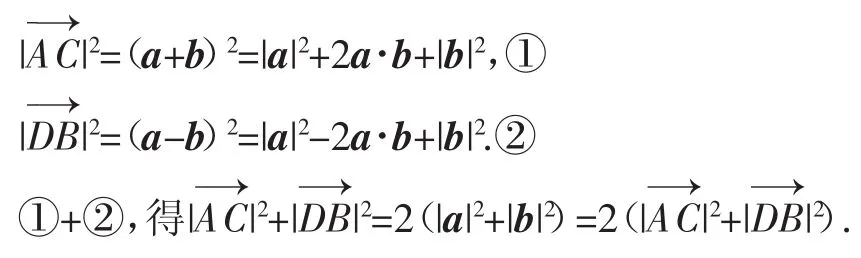
然而①-②可得另外一个结论：

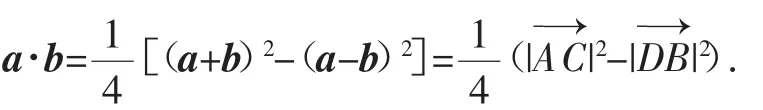
二、应用极化恒等式求向量的数量积

向量作为一种工具，由于它独特的性质，在全国各地的高考中成为创新命题的出发点，向量试题有着越来越综合、越来越灵活的命题趋势，极化恒等式成为越来越重要的考查点.

例1 （2012年浙江卷）在△ABC中，M是BC的中点，AM=3，BC=10，则________.

解析：如图2，因为M是BC的中点，连接AM，根据极化恒等式有

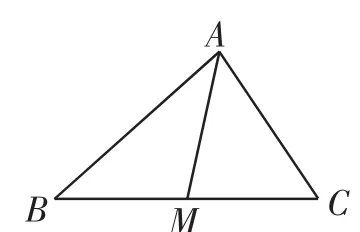
图2

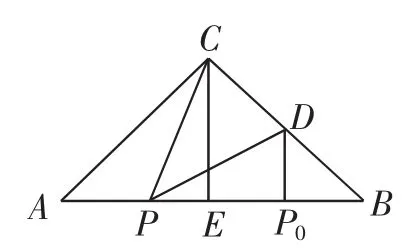
图3

例2 （2013年浙江卷）在△ABC中，P0是边AB上一定点，满足，且对于边AB上任一点P，恒有，则（ ）.

（A）∠ABC=90° （B）∠BAC=90°

（C）AB=AC （D）AC=BC

由几何性质知，P0D⊥AB，又因为CE平行P0D，所以CE⊥AB，故AC=AB，所以正确答案为D.

例3 （2016年江苏卷）如图4，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，则=_______.

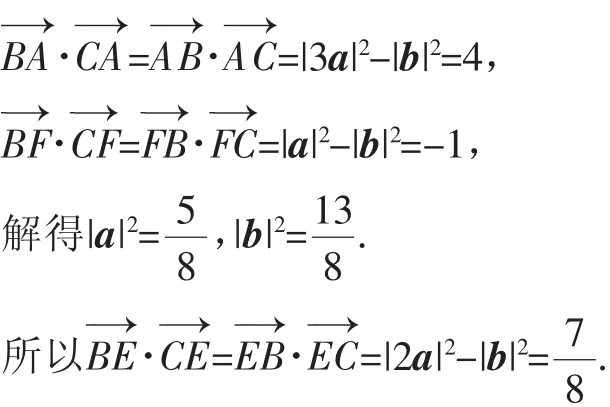
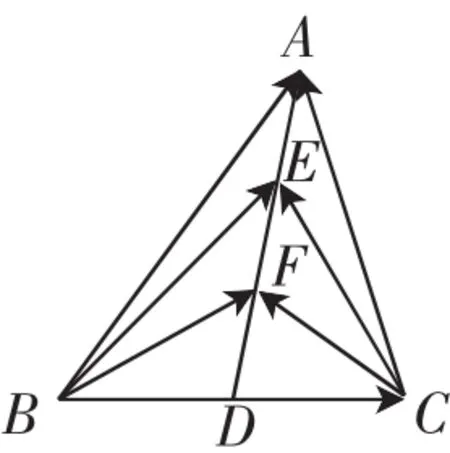
图4

三、应用极化恒等式求向量数量积的最值和范围

求解平面向量的数量积的最值和取值范围时可以从定义或坐标运算入手，但是解题过程常常会由于计算复杂、过程繁冗而导致出错，使用极化恒等式，往往能化繁为简，快速求解.

例4 已知正三角形ABC的外接圆O的半径为2，点P是圆O上的一个动点，则的取值范围是________.

解析：如图5，取AB的中点D，连接PD，O为△ABC的重心.因为△ABC为正三角形，所以O在CD上，OC=2OD=2，CD=3，AB=2，根据极化恒等式有：

图5

例5 （2012年安徽卷）平面向量a，b满足|2a-b|≤3，则的最小值为________.

评注：本题直接利用极化恒等式进行恒等变形，变形后对等式进行适当的放缩，要注意等号成立的条件.

例6 如图6，正方形ABCD的边长为4，动点P在以AB为直径的半圆弧上，则的 取 值 范 围 是________.

解析：取CD中点E，连接PE，在△PCD内根据极化恒等式有，由图6知，所以∈［0，16］.

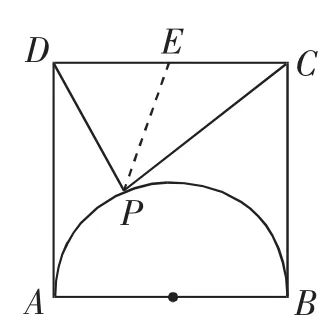
图6

评注：本题利用极化恒等式将向量的数量积进行代数转化，由于P是动点，就需要探求的取值范围.

例7 如图7，在△ABC中，点E，F分别是线段AB，AC的中点，点P在直线EF上，若S△ABC=2，则的最小值______.

解析：如图7，取BC中点D，在内根据极化恒等式有：

图7

例8 点P是棱长为1的正方体ABCD-A1B1C1D1的底面A1B1C1D1上的 一 点 ，则 向 量的取值范围是________.

评注：本题是极化恒等式在立体几何中的应用，题目比较简单，目的在于说明极化恒等式不仅适用于平面几何，也适用于空间几何.

例9（2017年全国卷Ⅱ）已知△ABC是边长为2的等边三角形，P为平面ABC内一点，的最小值为_______.

解析：如图8，设BC，AD的中点分别为D和E，连接PA，PB，PC，PD，PE，则，根据极化恒等式可得.因为△ABC是边长为2的等边三角形，所以，，当时的最小值为

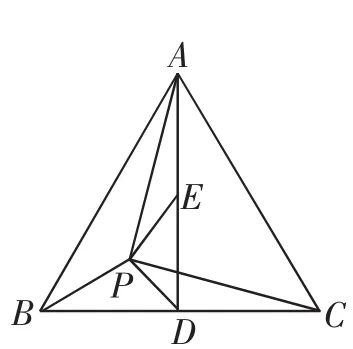
图8

极化恒等式不仅适用于平面向量，同样适用于空间向量，以上例题我们可以发现极化恒等式对于解决向量的数量积有着非常重要的作用，掌握了这种方法为解决向量数量积拓宽了思路和方法.

1.王宏权，李学军，朱成万.巧用极化恒等式，妙解一类高考题考题［J］.中学教研（数学），2013（8）.

2.单长松.平面向量中不得不提的一个恒等式［J］.中学教研（数学），2014（1）.

3.张城兵.极化恒等式的妙用［J］.高中数学教与学，2016（7）.

4.杨苍洲，周兰英.例谈极化恒等式的应用［J］.中小学数学：高中版，2016（10）.