数学欣赏视角下提升解题能力的实证研究*

☉江苏省太仓高级中学 张 敏

一、提升解题能力的重要意义

与初中数学不同，高中数学无论是内容上还是学习难度上都有明显的提升，知识点繁多，分布分散，使得高中数学的学习成为了一大难点.又因为数学学科在高考中所占的比重较大，因此也是学习的重点.尽管如此，高中数学的学习并不是毫无章法的，在解决不同类型的习题时可以寻找、总结出规律.

在教育改革不断深入的背景下，高中数学的学习不再局限于知识点的学习，培养学生的解题能力与提升学生的数学思维能力是当下高中数学教学的重点.数学是一门对学生的逻辑思维能力要求较高的学科，解题能力在一定程度上能体现学生的理论知识掌握情况.正因如此，全方位、多途径地提升学生的解题能力，才能使得学生更好地理解高中数学知识，提升应用数学的能力，把不同学习阶段的内容串联起来，形成一个完整的知识体系，在这个过程中也能形成适合自己的数学解题思想.

二、解题能力提升策略导向

（一）稳抓基础知识，加强理解学习

要想提升学生的解题能力，首先要做的就是强化学生对基础数学知识的掌握，加强学生对基础知识的学习，做到内化于心.笔者在教学过程中发现，很多数学习题都是教材中基础知识点的变换或变形，归根结底就是课本上的性质或定理，只是加上了具体的数学情境.尽管如此，在解决这些数学问题的过程中，有相当一部分的学生把这些“变形基础题”看成难题，这就说明这部分学生对于课本知识点掌握得不牢固，理解不深刻，看不出习题的本质所在.

在苏教版高中数学教材中，基础知识都比较简单，是学生学习高中数学的入门资料.尽管如此，在日常的教学过程中，教师不能忽略了教材基础知识，一味地求难、求异，只有强化基础训练，才能使得学生将理论知识融会贯通，在做题时能较快地想到解题思路.除此之外，数学教师在讲授过程中也要注意方法，在讲解习题时要引导学生总结习题背后的数学概念或基础定理、性质，让学生知其然，更知其所以然，提高解题能力.

（二）提升审题能力，明确解题方法

由于中学生的思维能力尚不发达，在题干要求比较复杂时，难免会存在理解不完全甚至理解错误的情况.因此，教师在强调审题的同时，要加强学生理解能力的培养，从根本上提升学生的审题能力.比如，苏教版高中数学选修的导数部分有这样一题：

（三）知识内容为主，思想方法为辅

高中数学知识点繁多，融合了代数、几何等诸多的知识，难度水平较高，因此对学生的基础知识掌握情况以及知识运用能力是较大的考验.尽管如此，知识点都是成体系的，不同的知识点、不同的习题都可能存在共通性，题目不同但采用的思想方法可能是相同的.因此，在日常的教学过程中，数学教师需要从思想方法着手，引导学生探索、总结有效的解题思路与解题方法.

1.方程与函数思想

函数思想就是对函数基础内容更深层次的概括，在不等式、数列、方程等内容中均有所体现.与函数思想相关的，方程思想也是现阶段高中数学学习中常用的思想方法，也是各地高考命题的重要内容.方程思想在各类数学计算题中应用广泛，能极大地展现学生的数学计算能力.对比各地历年的高考数学试题，笔者发现方程内容占比相当大.

综上，广大一线数学教师要注意学生函数思想和方程思想的培养.下面是苏教版数学教材中的应用实例：

例2 若不等式x2+ax+1≥0在范围内恒成立，试求a的最小值.

方法2：设函数y=x2+ax+1，结合二次函数图像分析，注意对称轴与区间]的相对位置关系，分三种情况讨论.

方法3：设函数y1=x2+1，y2=-ax，可将原问题转化为），可得a≥，即a的最小值为

2.分类讨论思想

分类讨论的解题思想的依据就是待解决对象的性质和特征，以此为基础，从多个情况对问题进行划分，单独分析，最终汇总得出结论.这一解题思想的一大特点就是涉及的数学知识点比较多，逻辑性与综合性较强，因此是对学生基础知识的掌握程度以及分类思想的直接体现.下面以苏教版教材中的数列问题为例.

在等差数列的教学过程中，根据公差的正负情况可以将等差数列分成递增数列、常数列以及递减数列；与此相类似的，对于等比数列，可以根据公比q以及首项a的范围对其进行分类：

如果a1＞0，q＞1或者a1＜0，0＜q＜1，那么该数列为递增数列；

如果a1＞0，0＜q＜1或者a1＜0，q＞1，那么该数列为递减数列；

如果q=1，那么该数列为常数列；

如果a1＜0，q＜1，那么该数列为摆动数列.

除此之外，在求等比数列前n项和Sn时，首先需要确定公比q的值是否等于1，若已知条件不能判断，则需要分成以下两种情况进行讨论：

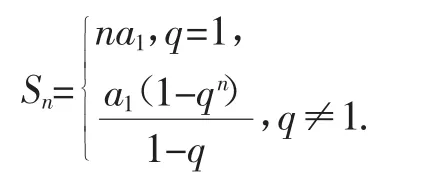
3.数形结合思想

在高中数学问题的解决过程中，数形结合这一解题思路极为实用.通过这一解题技巧，学生可以将代数与图形有机地结合起来，运用图像将题目中的代数关系直观描述.掌握数形结合的解题思想，准确运用图像与数量的相互关系，学生能厘清条件以及结论之间的层次关系，更好地解决这些问题.

【解答过程】题干中的已知函数可以理解成点（2，3）到动点（cosx，sinx） 的斜率. 因为cos2x+sin2x=1，所以动点（cosx，sinx）围成的轨迹是一单位圆，原问题也就转化成了点（2，3）到单位圆某一点连线的斜率问题.由图1可知，最大值与最小值分别出现在两切线处，解得原函数值域为y∈

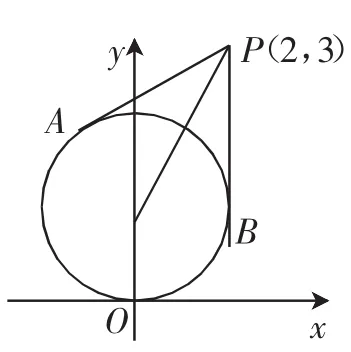
图1

4.转化思想

在做题过程中，常常会出现条件缺失或者是解题方法明确但解答过程繁杂的情况，这是教师就需要引导学生换个角度看问题，将问题进行转化，巧妙地解决问题，而不是一味地进行计算.

例4 a，b，c满足a2+b2+c2=ab+ac+bc，试判断长度为a，b，c的三边组成的△ABC的形状.

【解答过程】因为a2+b2+c2=ab+ac+bc，

所以2a2+2b2+2c2=2ab+2ac+2bc，

所以（a-b）2+（b-c）2+（a-c）2=0.

所以a=b，a=c，b=c，

所以△ABC为等边三角形.

四、结语

在高中数学的学习过程中，数学知识是基础，数学思想与解题能力是关键.为了有效地提升广大高中学生的数学解题能力，本文以苏教版高中数学教材为依托，从高中学生核心素养的要求出发，探索了数学解题能力的培养方法，通过具体数学案例详细介绍了常见的解题技巧，希冀切实提升高中学生的数学学习效率，强化高中学生的数学学习能力，引导学生积极主动地思考、学习，进而有效提升学生的数学学习成绩.