不经历风雨，也能见彩虹——对一道稽阳联考题的思考

☉浙江省诸暨市湄池中学 蔡旦燕

在教学中，我们总能发现，很多学生的运算能力真的太弱，知道解题的方法和思路，但在运算的具体实施中，过程烦琐，东漏西漏，花了好久时间还是算错，但就是坚持自己的思路对就一定能解出来，何况老师说过解析几何的计算就像经历一场暴风雨的洗礼，才能海阔天空见到彩虹.也认为这是通性通法，就是要经历复杂的计算.但事实上转化一下思路，就会发现不用经历复杂计算的洗礼，也能愉快地到达目的地，而且很多高考题、模考题、调研题看起来很普通，实际上却很漂亮，是命题专家经过精心思考命制出来的，有很大的研究空间和教学价值.本文从稽阳联考的一道求解离心率的选择题出发，将题目所给的条件灵活转化为解三角形，不用再联立方程组解点坐标.

一、试题展示

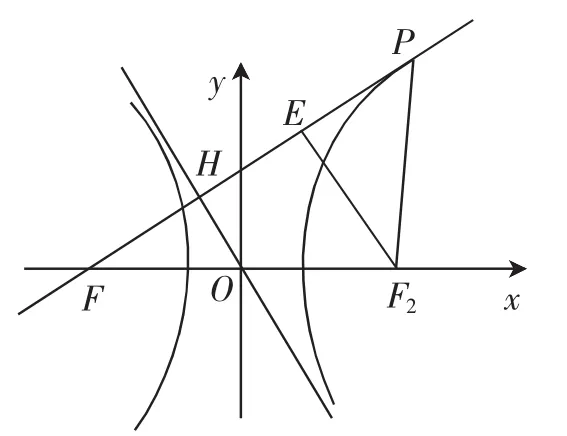
图1

分析2：F2为双曲线的右焦点，因为FH⊥PF，所以|FH|=b，则|OH|=a.又因为所以|PF|=3b，根据双曲线定义知|PF2|=3b-2a.在Rt△OFH中，.在△PFF2中，利用余弦定理得到cos∠PFF2=，而它们相等，很容易得到2b=3a，从而得到离心率.这就转化到解三角形问题了.

分析3：如图1，还可以取PH的中点E，则根据相似比|EF2|=2a，而且EF2⊥PF，所以在Rt△PEF2中，（EF2）2+（PE）2=（PF2）2，即（2a）2+b2=（3b-2a）2，计算更加简单.

点评：这种解法思路非常清晰，根据联立直线方程可得点坐标，再根据向量共线，得出点P的坐标代入双曲线方程就得到a，b，c的关系式，化解可得结果.但在实际操作过程中，学生遇到了几个难关，现在的学生计算能力比较差，尤其是纯粹的字母运算，求点H的坐标还可以，求点P的坐标时就出现了问题，还有一个问题是代入双曲线方程后化解不了.结果就是花了好多时间还是没有得到正确答案，以至于做后面的题目就没有时间了，而且心浮气躁，影响考试的情绪.

那么我们转化一下思路，放到双曲线的本质上去，到平面内两定点的距离之差的绝对值是定值.而且双曲线的焦点到渐近线的距离为b，这里出现了一个直角三角形，根据相似比，我们知道了一个三角形的各边的长度，利用余弦定理转化为了解三角形的问题.而在分析3中构造一个Rt△PEF2，计算更加的简洁明了.

二、类题再现1

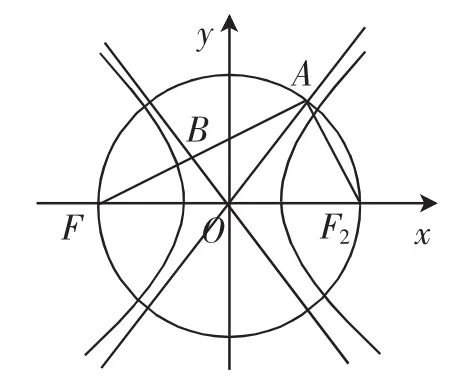
图2

点评：分析1完全是题目的直译，根据相交求出点坐标，根据向量相等得到坐标之间的等式，但计算复杂.分析2注意到等腰三角形的三线合一，利用垂足，可以少算一个点坐标，计算量大大地减少.而分析3巧妙地注意到这个图形的特殊性以及渐近线特征，得到△OAF2为正三角形，马上可以得到渐近线的斜率.

三、类题再现2

类题2 （2015年浙江省数学高考文科试题第15题）椭圆的右焦点F（2c，0），关于直线的对称点Q在椭圆上，则椭圆的离心率为_________.

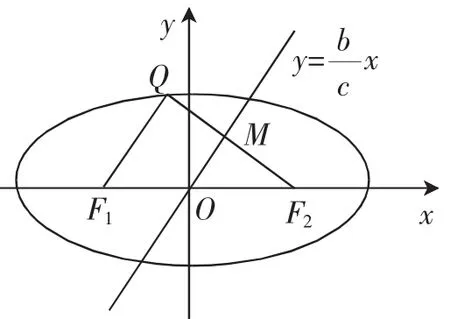
图3

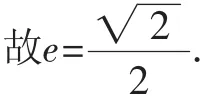
点评：本题跟前一题一样，直译题意就是求对称点，然后把对称点代入椭圆方程得到a，b，c之间的关系，但求解点也好，化简也好，大部分学生花了九牛二虎之力还是解决不了.但第二种解法把点关于直线对称的条件等价转化，得到中位线，从而有相似比，再利用椭圆定义，得到a，b，c之间的关系，计算量大大减少.

反思感悟：从这几题的解答可以看出，对于求这样一类圆锥曲线的离心率问题，即条件中有点关于直线对称或者说有几等分点出现，不一定要求出点的坐标，代入方程进行复杂的字母计算，才能得出我们的答案.我们往往可以根据相似比来得出线段长度之间的关系，或者根据直角三角形的勾股定理，或者利用一般三角形的余弦定理等价转化、数形结合得出一个含有a，b，c或其中任意2个的关系式，从而算出离心率.这种办法才是我们优先考虑的办法.也就是说烦琐的办法，直译的办法不一定就是通性通法，简洁有效的办法也是通性通法.这就需要我们平时在教学中，应鼓励学生积极参与，百家争鸣，更要引导学生从中提炼、总结出最初、最基本的数学概念，最自然、最优化的解题方法.逐步达到做一题，会一类，用一法，解多题的境界.这样不仅能让学生摆脱题海战术，而且对于以后学习新的知识有了方向，求同思维大大发展.同时需要我们长期有意识地营造氛围，让学生不时地感悟题目中所蕴含的数学思想方法，自然而然地掌握它.不经历烦琐计算的风雨洗礼，也能见到美丽的彩虹，甚至是更快地见到它！

1.中华人民共和国教育部.普通高中数学课课程标准（试验）［M］.北京：人民教育出版社，2004.

2.谢全苗.数学解题教学中要辩证地看待“通法”与“巧法”［J］.数学通报，2001（6）.F