线性代数中矩阵特征值的解析方法
朱韬
(安徽新华学院国际教育学院,安徽 合肥 230088)
一、三次多项式的对称点概述
对于三次多项式ax3+bx2+cx+d(a=0)如果存在某一实数x0,对任意x 都有a(x0-x)3+b(x0-x)2+c(x0-x)+a(x0+x)3+b(x0+x)2+c(x0+x)=2ax30+2bx20+2cx0成立, 就称x0为此三次多项式的对称点。例如, 三次多项式x3-3x2+2x+1, 实数1 满足(1-x)3-3(1-x)2+2(1-x)+(1+x)3-3(1+x)2+2(1+x) = 2×13+2×(-3)×12+2×1×1,那么实数1 就是三次多项式x3 - 3x2 + 2x + 1 的对称点.附注如果实数x0 是三次多项式的对称点, 那么有ax3 + bx2 + cx + a(2x0 - x)3 + b(2x0 - x)2 + c(2x0 - x)=2ax30+ 2bx20+ 2cx0只需要把a(x0-x)3+b(x0-x)2+c(x0-x)+a(x0+x)3+b(x0 + x)2 + c(x0 +x) = 2ax30+ 2bx20+ 2cx0 中的x 换为x0-x 即可证明.
二、三次多项式的对称点性质分析
性质一三次多项式ax3 + bx2 + cx + d (a = 0) 的对称点- b3a是三次函数f(x) = ax3 + bx2 + cx + d (a = 0) 二阶导数f′′(x) = 6ax + 2b 的零点.
性质二三次多项式ax3 + bx2 + cx + d (a = 0) 的对称点是三次函数f(x) = ax3 + bx2 + cx + d (a = 0) 一阶导数f′(x) = 3ax2 + 2bx + c 的对称轴x = - b3a.
性质三若三次函数f(x) = ax3 + bx2 + cx + d (a =0) 有两个极值点, 分别为x1, x2, 那么有x1 + x22=- b3a,f(x1) + f(x2)2= f(x1 + x22).
三、三次多项式的对称点的存在性
证明1 假设ax3 + bx2 + cx + d (a = 0) 那么对于任何一个变量x, 都有a(x0 - x)3 + b(x0 - x)2 + c(x0 - x) +a(x0 + x)3 + b(x0 + x)2 + c(x0 + x) = 2ax30+ 2bx20+ 2cx0,经过整理化简得x0 = - b3a.因此可以知道任何一个三次多项式ax3 + bx2 + cx +d (a = 0) 存在唯一对称点- b3a.证明2 a(0 - x)3 + c(0 - x) + a(0 + x)3 + c(0 + x) =2a×03 +2c×0, 因此三次多项式ax3 +bx2 +cx+d (a = 0)在b = 0 时, 也就是缺少二次项时, 有唯一对称点0. 在解一元三次方程ax3 + bx2 + cx + d = 0 (a = 0) 的时候, 是采用差根变换, 各根减去- b3a, 可得缺二次项的三次方程(未知元用x′表示, 即x′= x - b3a):
ax′3 + apx′+ aq = 0,其中p =3ac - b23a2 , q =2b3 - 9abc + 27a2d27a3 . ax′3 + apx′+aq 有唯一对称点0. 那么ax3+ bx2+ cx + d = 0 (a -= 0) 有唯一对称点- b3a.
证明3 三次函数的对称中心的横坐标就是三次函数所对应的三次多项式的对称点, 观察三次多项式ax3 + bx2 + cx + d (a = 0) 所对应的三次函数f(x) = ax3 + bx2 + cx + d (a = 0) 的图像, 可以知道函数图像在对称中心左右两边的凹凸性是相反的, 如果a > 0, 函数在对称中心的左边是凸函数, 在x自变量不断变大时,会导致切线斜率变小,对三次函数进行二阶求导,导数<0;而对称中心右侧为凹函数,x自变量变大时,会导致切线斜率随之变大,对三次函数进行二阶求导,导数>0;如果a < 0, 函数在对称中心的左边是凹函数, 随着自变量x 增大, 切线的斜率增大, 三次函数的二阶导数>0, 而在对称中心右侧为凸函数,在x自变量不断变大的过程中,会导致切线斜率不断变小,对三次函数进行二阶求导,导数f′′(x)<0[1]。由此可以得知,对称中心下的三次函数的二阶导数位置为零,所以三次多项式ax3 + bx2 + cx + d (a = 0) 的对称点可以求出三次函数f(x) = ax3 + bx2 + cx + d (a = 0) 的二阶导数f′′(x) 零点,其即为多项式对称点所在。综上所述,能够明确对于所有三次多项式来说,ax3 +bx2 +cx + d (a = 0) 存在唯一对称点-b3a.
四、三次多项式的因式分解U 型方法
对A=2-2 0-2 1-2 0-2 1 0 进行特征值计算时,得|A-λE|=2-λ-20-21-λ-20-2-λ,整理-λ3+3λ2+6λ-8=0。对该三次多项式借助U 型法进行分解,-1,3,6,-8四个系数为一行,找到乘积是-8×-1的数字,包括-1、-8和- 2、- 4等,该题中为1、8及- 2、- 4。若选- 2 ,- 4 这一组。- 2 放在3 下面,- 4 放在6 下面,然后3 减去-2 等于5,6 减去- 4 等于10,选- 2 ,- 4 这一组, 就是要满足-1-2=510=-4-8现在我们把式子写出来我们可以用笔依次连接- 1,- 2,5 ,10 . -4 ,-8 ,表示为U形[3]。借此转化多项式,可得3λ2和6λ为- 2λ2 + 5λ2和10λ- 4λ,由此得到-λ3-2λ2+5λ2+10λ-4λ-8=0下面分组(-λ3-2λ2)+(5λ2+10λ)-(4λ+8)=0每组提公因子得-2λ(λ+2)+5λ(λ+2)-4(λ+2)=0, 再提公因子得-(λ+2)(λ2+5λ-4)=0后面再对二次多项式用十字相乘法因式分解得-(λ+2)(λ-1)(λ-4)=得到特征值λ1=-2,λ2=1,λ3=4。对于乘积是-8×-1的数字,若选择的是2、4,则3之下为2,6下为4,3-2=1,6-4=2,按U 型
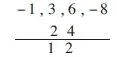
——从广州一模的一道选择题谈起

