例谈数学核心素养在高中数学试题中的体现

☉甘肃省秦安县第二中学 罗文军

新课标修订组认为：数学核心素养是具有数学基本特征的，适应个人终身发展和社会发展需要的人的思维品质与关键能力.高中阶段数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.在高中数学学习中，通过解题提高自身的数学核心素养，是每位同学都必须面对的问题.本文结合具体试题来谈一下高中数学试题中是如何体现核心素养的.

一、数学抽象

数学抽象是指舍去事物的一切物理属性，得到数学研究对象的素养.主要包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，用数学语言予以表征.

得1≤x＜2，故答案为［1，2）.

评注：本题从具体的题设背景中，联想导数的运算法则［f（x）·g（x）］′=f′（x）·g（x）+f（x）·g′（x），抽象出函数g（x）=x·f（x），体现了数学抽象的核心素养.本题主要考查利用导数研究函数的单调性、构造函数解不等式，属于难题.联系已知条件和结论，构造辅助函数是高中数学中一种常用的方法，解题中若遇到有关不等式、方程及最值之类的问题，设法建立起目标函数，并确定变量的限制条件，通过研究函数的单调性、最值等问题，常可使问题变得明了，准确构造出符合题意的函数是解题的关键.解这类不等式的关键点也是难点就是构造合适的函数，构造函数时往往从两方面着手：①根据导函数的“形状”变换不等式“形状”；②若是选择题，可根据选项的共性归纳构造恰当的函数.

二、逻辑推理

逻辑推理是指从一些事实和命题出发，依据规则推出其他命题的素养.主要包括两类：一类是从特殊到一般的推理，推理形式主要有归纳、类比；一类是从一般到特殊的推理，推理形式主要有演绎.

例2 已知数列｛an｝满足a1=1，an+1=3an+1.

评注：第（1）问中，通过递推关系式构造出一个我们比较熟悉的数列，从而求出数列的通项公式，运用了演绎推理的方法，体现了逻辑推理的核心素养，也体现出数学抽象的核心素养.第（2）问运用了将分母缩小的放缩法，将复杂问题简单化，证明不等式的过程运用了演绎推理，体现了逻辑推理的核心素养.

三、数学运算

数学运算是数学活动的基本形式，数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.数学中的运算主要有两大类：一类是纯代数运算；一类是借助几何图形进行的代数运算.

（1）求椭圆Γ的方程；

（2）直线l与圆O：x2+y2=b2相切于点M，且与椭圆Γ相交于不同的两点A，B，求|AB|的最大值.

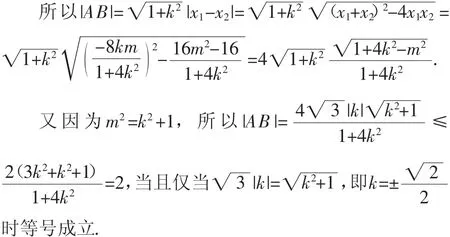
综上所述，|AB|的最大值为2.

评注：本题主要考查直线与圆锥曲线的位置关系，所使用的方法为韦达定理法：因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点及弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用.第（1）问和第（2）问的解答过程中，都是借助几何图形进行的代数运算，考查了运算求解能力，体现了数学运算的核心素养.解析几何的运算通常集“繁、长、巧”于一体，让很多同学望而生畏.究其原因，主要是同学们在运算长度的判断上出了问题：不能预估选择的解题方向会有怎样的运算及运算长度.若在解题过程中，同学们能认识到解题环节产生的运算，并通过分析进行合理的调控，更深入地理解算理，这样才可以提高运算的灵活性.

四、数据分析

数据分析是指针对研究对象获取数据，运用统计方法对数据进行整理、分析和推断，形成关于研究对象知识的素养.主要包括：收集数据，整理数据，提取信息，构建模型，进行推断，获得结论.

例4 （河南省长葛市一高2018届高三上学期开学考试）共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务，是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本（单位：元）与租用单车的数量（单位：千辆）之间的关系”进行调查研究，在调查过程中进行了统计，得出相关数据见下表：

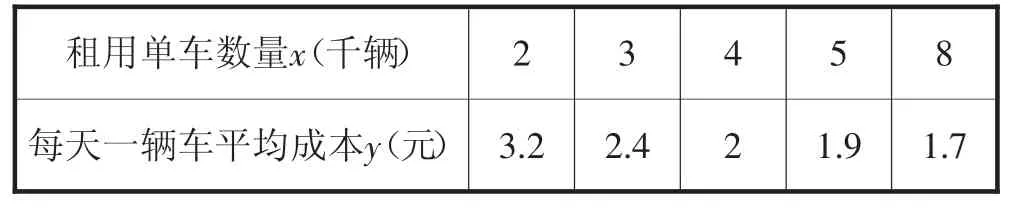
租用单车数量x（千辆） 2 3 4 5 8每天一辆车平均成本y（元） 3.2 2.4 2 1.9 1.7

根据以上数据，研究人员分别借助甲、乙两种不同的回归模型，得到两个回归方程，方程甲：，方程乙（1）为了评价两种模型的拟合效果，完成以下任务：①完成下表（计算结果精确到0.1）（备注：e^i=yi-y^i，e^i称为相应于点（xi，yi）的残差（也叫随机误差））；

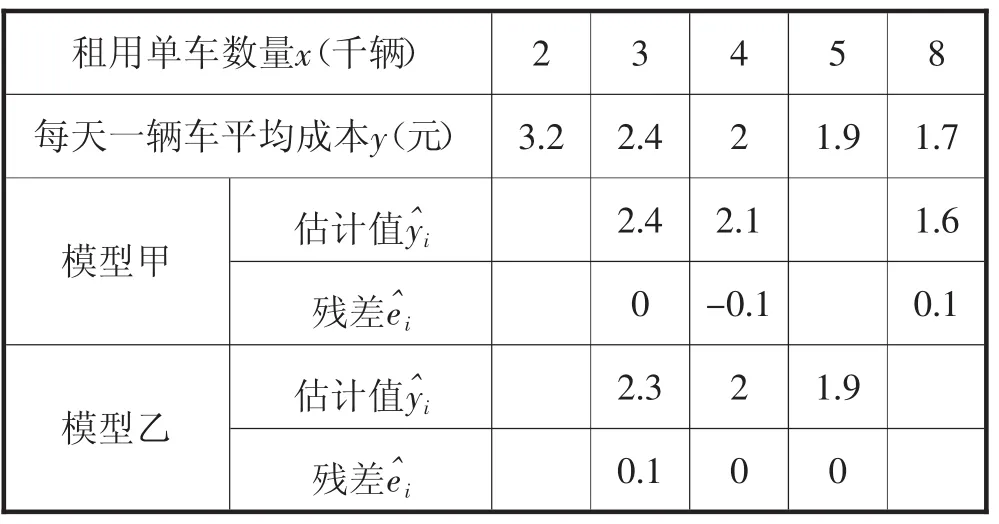
租用单车数量x（千辆） 2 3 4 5 8每天一辆车平均成本y（元） 3.2 2.4 2 1.9 1.7模型甲 估计值y^i 2.4 2.1 1.6残差e^i 0 -0.1 0.1模型乙 估计值y^i 2.3 2 1.9残差e^i 0.1 0 0

②分别计算模型甲与模型乙的残差平方和Q1及Q2，并通过比较Q1，Q2的大小，判断哪个模型拟合效果更好.

（2）这个公司在该城市投放共享单车后，受到广大市民的热烈欢迎，共享单车常常供不应求，于是该公司研究是否增加投放.根据市场调查，这个城市投放8千辆时，该公司平均一辆单车一天能收入10元，6元的概率分别为0.6，0.4；投放1万辆时，该公司平均一辆单车一天能收入10元，6元的概率分别为0.4，0.6.问：该公司应该投放8千辆还是1万辆能获得更多利润？（按（1）中拟合效果较好的模型计算一天中一辆单车的平均成本，利润=收入-成本）.

分析：（1）①通过对回归方程的计算可得两种模型的估计值y^i，代入e^i=yi-y^i，即可得残差；②计算可得Q1，Q2，比较Q1与Q2的大小可知哪种模型的拟合效果更好；（2）分别计算投放8千辆和1万辆时该公司一天获得的总利润，即可得结论.

解：（1）①经计算，可得下表：

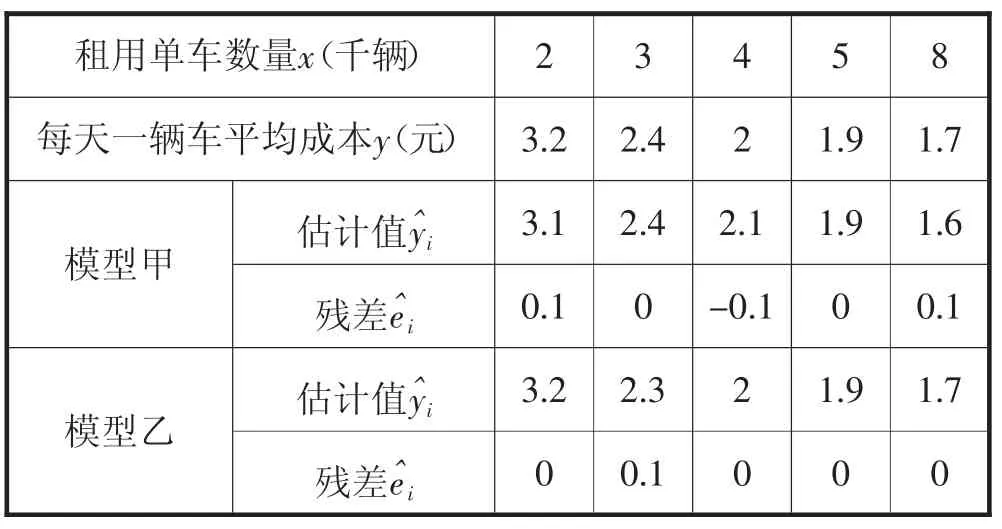
租用单车数量x（千辆） 2 3 4 5 8每天一辆车平均成本y（元） 3.2 2.4 2 1.9 1.7模型甲 估计值y^i 3.1 2.4 2.1 1.9 1.6残差e^i 0.1 0 -0.1 0 0.1模型乙 估计值y^i 3.2 2.3 2 1.9 1.7残差e^i 0 0.1 0 0 0

②Q1=0.12+（-0.1）2+0.12=0.03，Q2=0.12=0.01. 因为Q1＞Q2，故模型乙的拟合效果更好.

（2）若投放量为8千辆，则公司获得每辆车一天的收入期望为10×0.6+6×0.4=8.4，所以一天的总利润为（8.4-1.7）×8000=53600（元）.

所以投放1万辆能获得更多利润，应该增加到投放1万辆.

评注：本题主要考查了回归模型的残差分析及概率中的数学期望.本题主要涉及数据分析的数学核心素养.其中第（1）问的第①小问中分别计算模型甲和模型乙的估计值和残差，可以看成是数据分析中的整理数据和提取信息；第（1）问的第②小问中计算模型甲与模型乙的残差平方和Q1及Q2，并比较Q1，Q2的大小，可以看成数据分析中的构建模型、进行推断、获得结论，最终得出的结论是模型乙的拟合效果更好.第（2）问中，利用模型，计算每辆车一天收入的数学期望，再计算出总利润，比较利润大小，得出选择投放1万辆.

五、直观想象

直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的素养.直观想象是发现和提出问题、分析和解决问题的重要手段，是探索和形成论证思路、进行数学推理、构建抽象活动的思维基础.

例5 （云南师范大学附属中学2018届高考适应性月考）如图1，在长方体ABCD-A1B1C1D1中，A1C与平面A1ADD1及平面ABCD所成角分别为30°，45°，M，N分别为A1C与A1D的中点，且MN=1.

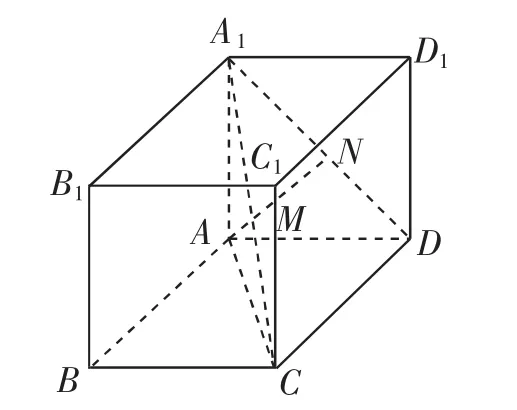
图1

（1）求证：MN⊥平面A1ADD1；

（2）求二面角A-A1C-D的平面角的正弦值.

分析：（1）根据中位线定理可得MN//CD，由长方体的性质可得CD⊥平面A1ADD1，从而可得结果；（2）以AB，AD，AA1所在直线为x，y，z轴建立空间直角坐标系A-xyz，分别求出平面A1CD与平面A1AC的一个法向量，根据空间向量夹角的余弦公式及同角三角函数之间的关系，可得结果.

解：（1）在长方体ABCD-A1B1C1D1中，因为M，N分别为A1C，A1D的中点，所以MN为△A1CD的中位线，所以MN∥CD.

又因为CD⊥平面A1ADD1，所以MN⊥平面A1ADD1.

（2）在长方体ABCD-A1B1C1D1中，因为CD⊥平面A1ADD1，所以∠CA1D为A1C与平面A1ADD1所成的角，即∠CA1D=30°.

又因为A1A⊥平面ABCD，所以∠A1CA为A1C与平面ABCD所成的角，即∠A1CA=45°.

所以MN=1，CD=2，A1C=4，A1A=，AC=.

如图2，分别以AB，AD，AA1所在直线为x，y，z轴建立空间直角坐标系A-xyz，所以A（0，0，0），D（0，2，0），C（12，，C（2，2，0），B（2，0，0）.

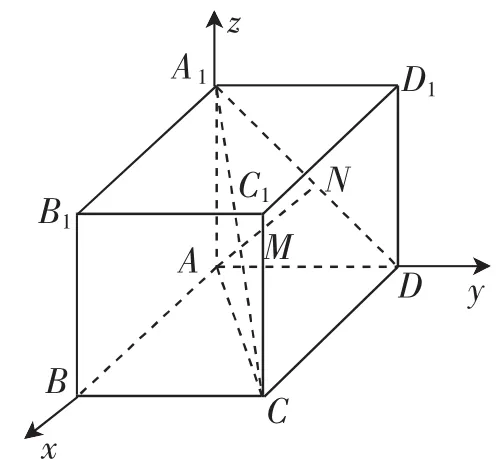
图2

评注：本题主要考查线面垂直的判定、利用空间向量求二面角，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，从而建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组，求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.本题第（1）问利用几何直观，借助题设和图形中的平行关系和垂直关系，利用了线面垂直的性质定理证明了线面垂直.第（2）问利用几何直观建立空间直角坐标系，利用法向量法，将几何问题代数化，体现出直观想象和数学运算的核心素养.

六、数学建模

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的素养.

例6（江苏省常州市横林高级中学2017～2018学年第一学期高三月考）某农户准备建一个水平放置的直四棱柱形储水器（如图3），其中直四棱柱的高AA1=10m，两底面ABCD与A1B1C1D1是高为2m，面积为10m2的等腰梯形，且若储水窖顶盖每平方米的造价为100元，侧面每平方米的造价为400元，底部每平方米的造价为500元.

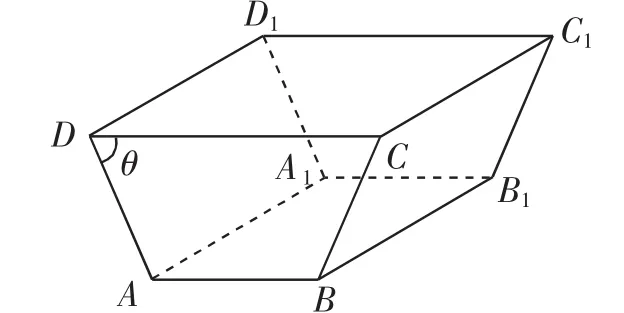
图3

（1）试将储水窖的造价y表示为θ的函数；

（2）该农户如何设计储水窖，才能使得储水窖的造价最低，最低造价是多少元？（取=1·73）

分析：（1）过A作AE⊥DC，垂足为E，令AB=x，先将x用θ表示，再求出CD，即可将储水窖的造价y表示为θ的函数；（2）利用导数确定函数的单调性，即可求出θ为何值时有最小值，从而可得如何设计储水窖，才能使得储水窖的造价最低.

解：（1）如图4，过A作AE⊥DC，垂足为E，则AE=2，

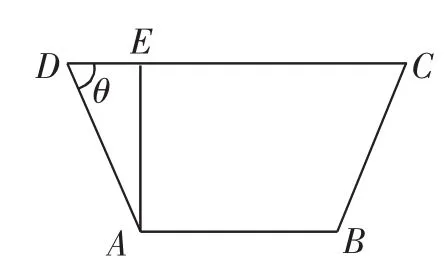
图4

答：当∠ADC=60°时，造价最低，最低造价为51840元.

评注：本题主要考查阅读能力及数学建模能力、函数的解析式，属于难题.与实际应用相结合的题型也是高考命题的动向，这类问题的特点是通过现实生活的实例考查书本知识，解决这类问题的关键是耐心读题、仔细理解，只有吃透题意，才能将实际问题转化为数学模型进行解答.解答本题的根据是将储水窖的造价y表示为θ的函数，从而利用导数求最小值.本题也考查了数学应用能力和创新意识.

1.中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.北京:人民教育出版社，2017.F