错在哪里
2019-02-21 07:44:28
中学数学教学 2019年1期
1 黑龙江省鸡西市第一中学数学教研室 (邮编:158100)
题目已知E、F、G、H、M、N分别为正四面体ABCD的棱AB、BC、CD、DA、AC、BD的中点,这4个顶点和6个中点共可确定( )对异面直线.
A.423 B.399 C.379 D.255
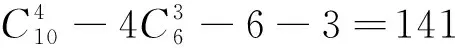
解答错了,错在哪里?
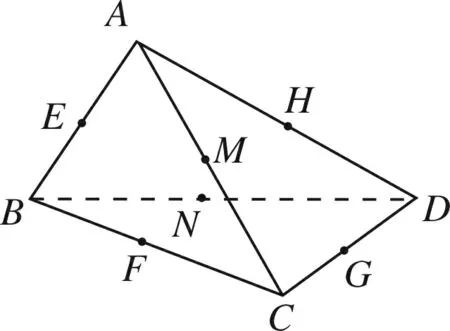
图1
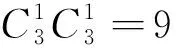
下面就按照所成角的大小对这255对异面直线进行归类梳理,希望这些结论能大家的教学或学习有所帮助.
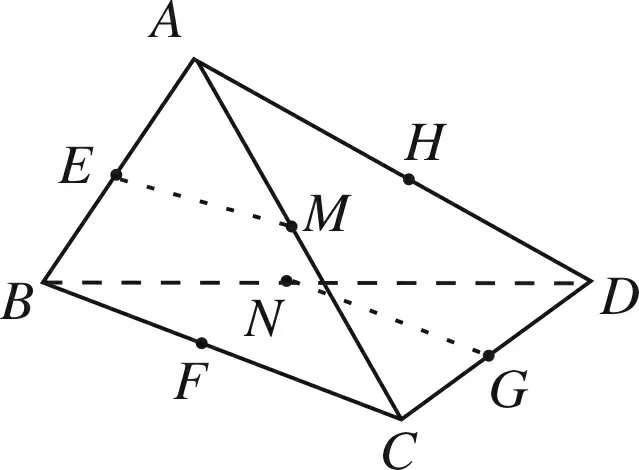
图2
第一类 成角为900
(1)易知正四面体ABCD的对棱确定的3对异面直线成角为900;
(2)如图2所示,直线AD与直线EM,NG成900角,这种情况共有6×2=12对;
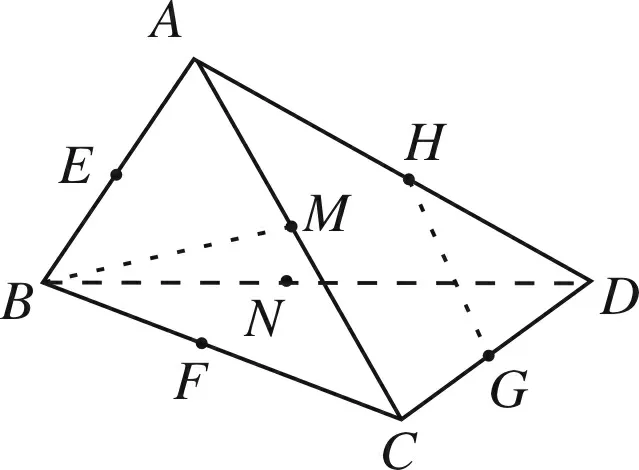
图3
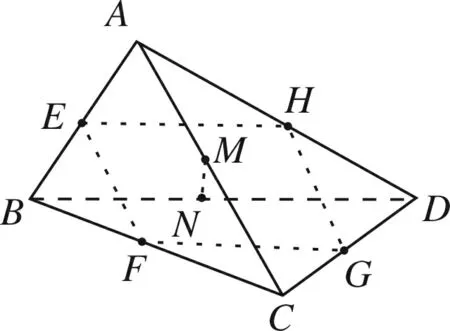
图4
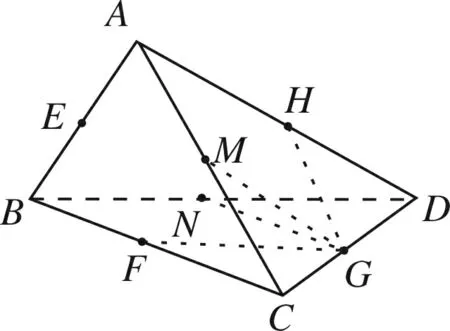
图5
(3)如图3所示,直线BM与直线GH成900角,这种情况共有3×4=12对;
(4)如图4所示,易知直线MN⊥截面EFGH,即直线MN与直线EF,FG,GH,HE均成900角,这种情况共有3×4=12对;
综合(1),(2),(3),(4)可知在这255对异面直线中,成角为900的共有39对.
第二类 成角为600
(1)如图5所示,直线AB与直线GM,GH,GN,GF成角均为600,这种情况共有6×4=24对;
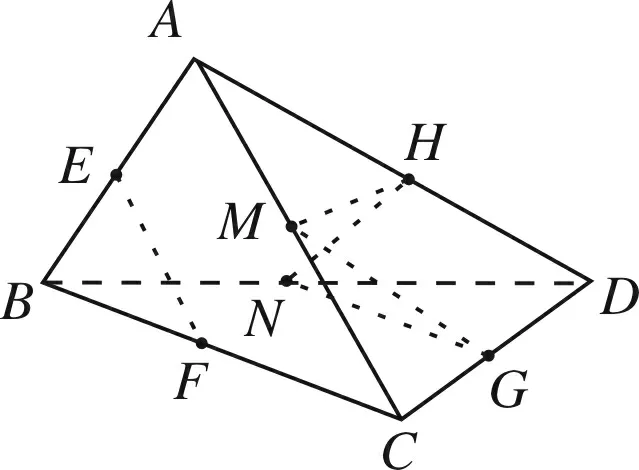
图6
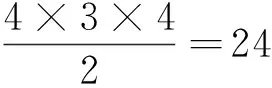
综合(1),(2)可知这255对异面直线中,成角为600的共有48对.
第三类 成角为450
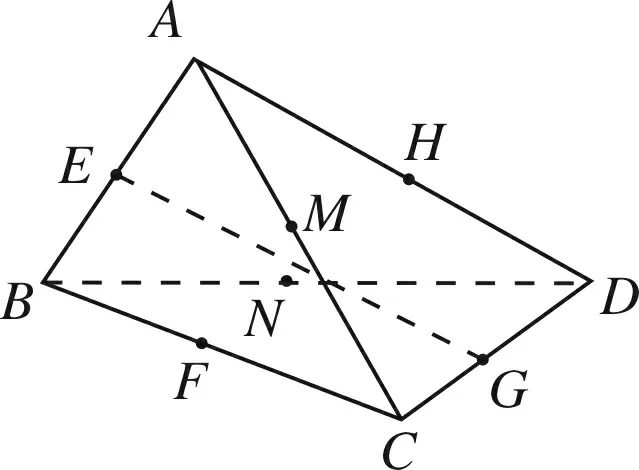
图7
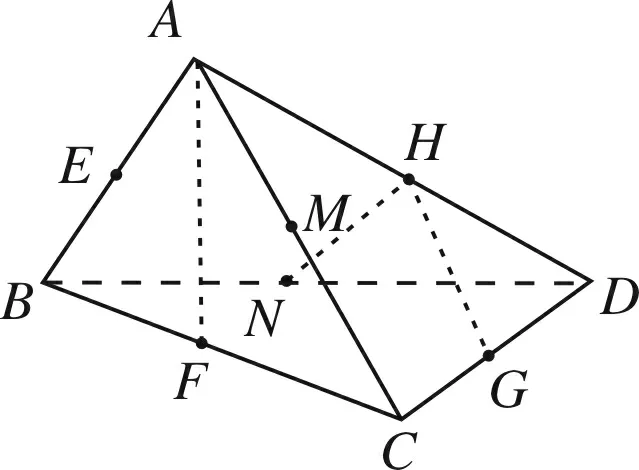
图8
如图7所示,直线EG与直线AC,BD所成的角均为450,这种情况共有6×2=12对;
第四类 成角为300
如图8所示,直线AF与直线HN,HG所成的角分别为300,这样的情况共有6×2=12对;
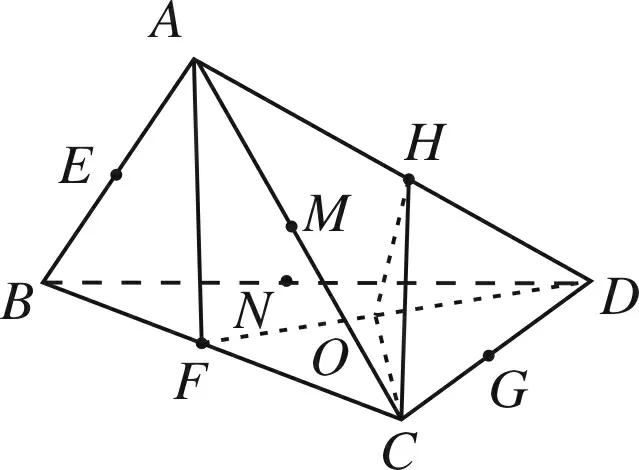
图9
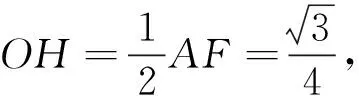
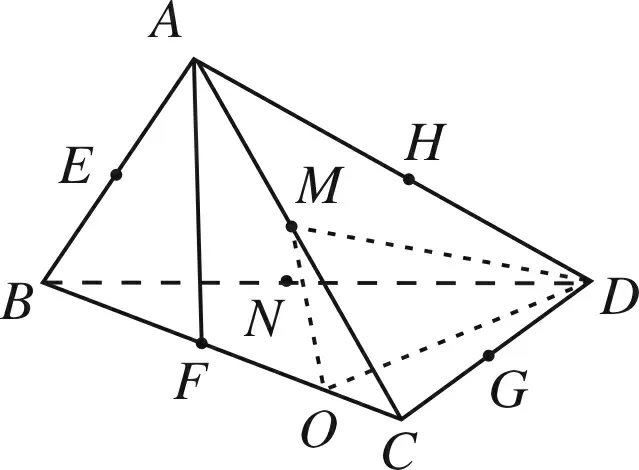
图10
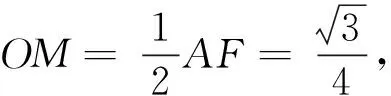
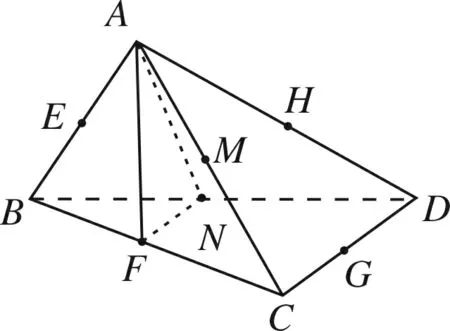
图11
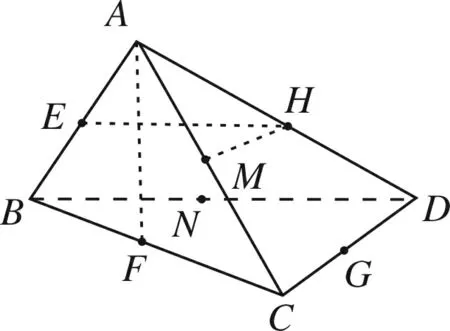
图12
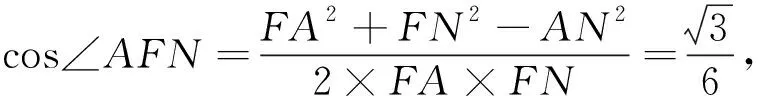
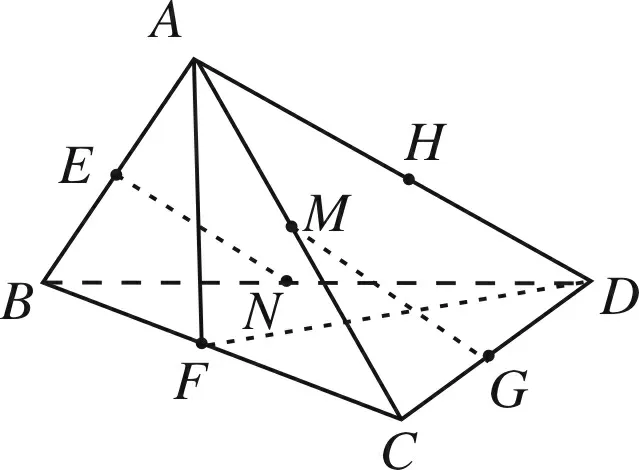
图13
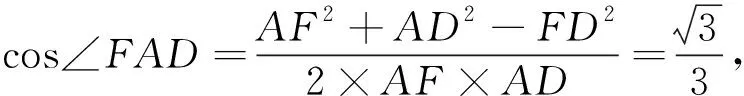
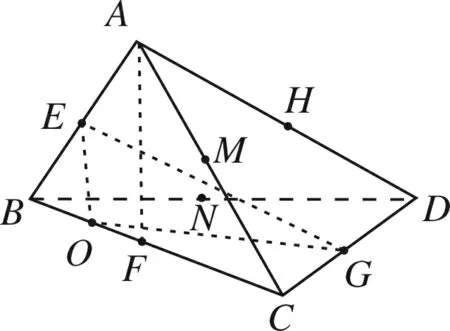
图14
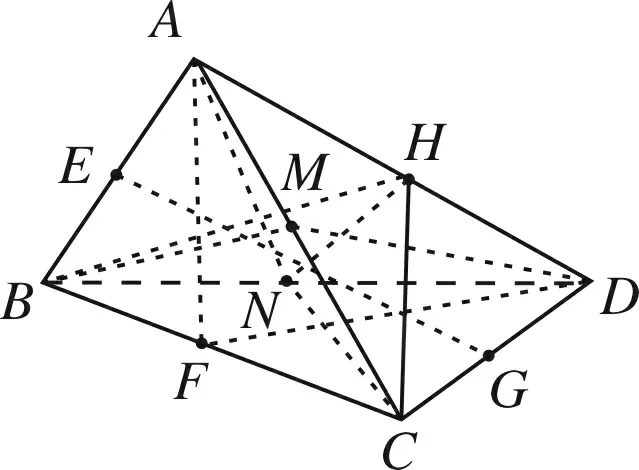
图15
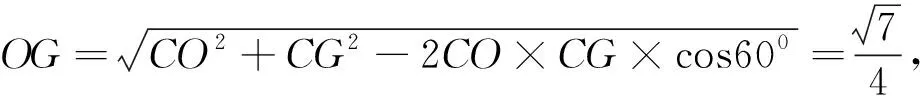
从上述分类可以看出这是一道内涵极其丰富的题目,有兴趣的读者,还可再进一步深刻挖掘,一定会得到更多好的结论,这些结论都是我们进行巩固练习和习题编制的绝好素材.
猜你喜欢
中学数学研究(2024年4期)2024-05-23 13:15:19
聊城大学学报(自然科学版)(2022年2期)2022-11-19 07:03:54
数理天地(高中版)(2022年9期)2022-07-24 05:56:01
语数外学习·高中版上旬(2020年8期)2020-09-10 07:22:44
中学生数理化(高中版.高二数学)(2018年2期)2018-04-04 05:12:28
戏曲研究(2017年3期)2018-01-23 02:50:52
青苹果·教育研究版(2016年6期)2016-12-02 09:15:30
高中生学习·高二版(2016年9期)2016-05-14 00:13:04
中学生数理化·高一版(2016年11期)2016-03-01 03:46:00
中学数学研究(2008年9期)2008-12-09 03:32:30

