两等圆中“等角对等弦”之应用

王德礼

安徽省宿州市萧县耿庄小学 (邮编：235232)

初中数学教材九年级上册中，关于圆周角定理有一个重要的推论：在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等.这个定理又可简记为：等角对等弧或等角对等弦.这个定理的前提条件是：“同圆或等圆中”，平时最常见的都是在同圆中来应用，在不同的等圆中几乎没用过.在非同等圆中，这个定理好像无用武之地，事实并非如此.下面略举几例为之正名.

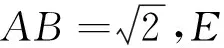
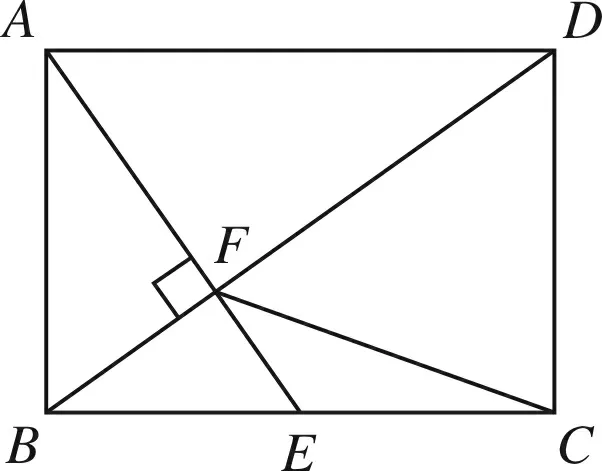
解析如图2，连接DE，

因为E是矩形ABCD边BC的中点，由矩形的对称性可知：DE=AE，

所以Rt△ABE和Rt△DCE的外接圆是等圆(直径AE=DE)，

因为∠DCE=∠BFE=90°，

所以∠AEB=∠CDF(即两等圆中的等角)，

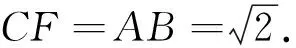
本例当然还有其他解法，在此不作讨论(下同，所有例题不谈其他解法)，用“等角对等弦”来解决，新颖别致，简洁明快！

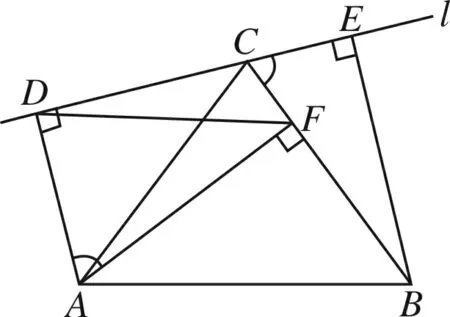
图3

例2如图3，△ACB中，CA=CB，AF是高，直线l过点C，过A、B两点向l作垂线，垂足分别为D、E，连接DF．求证：DF=BE.

解析因为∠ADC=∠AFC=90°，

所以∠DAF+∠DCF=∠BCE+∠DCF=180°，所以∠DAF=∠BCE.

又因为CA=CB，所以Rt△ACD和Rt△BCE的外接圆是等圆，所以DF=BE.

本例用“等角等弦”，一步到位，干脆利落，不需添加辅助线，要比其它方法来的直接.

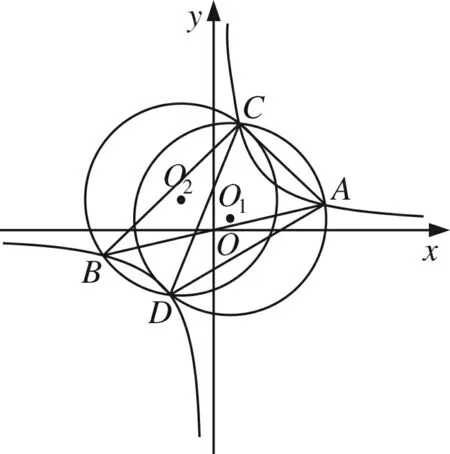
图4

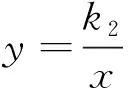
求证：△ACD的外接圆与△BCD的外接圆的半径相等.

这题将双曲线、圆和直线形结合，难度较大，初看似乎无处下手.若用“等角对等弦”，则可显示其威力非凡！

在解这道题之前，需要先介绍双曲线的一个性质.

双曲线等角定理双曲线上的任意一点向双曲线上一对中心对称点引直线，这两条直线与同一坐标轴相交成等角.下面仅给出该结论的一种证法：

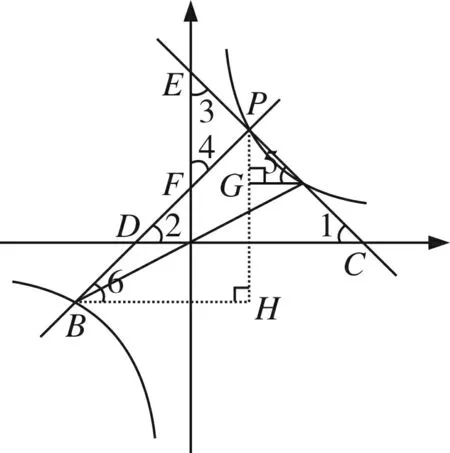
图5

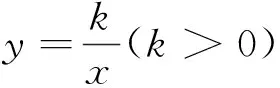
证明过P作x轴的垂线PH，分别过A、B向PH作垂线，垂足分别为G、H.

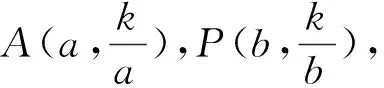
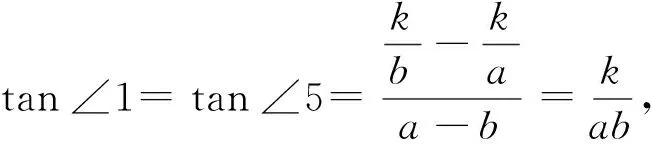
所以∠1=∠2；同理∠3=∠4.

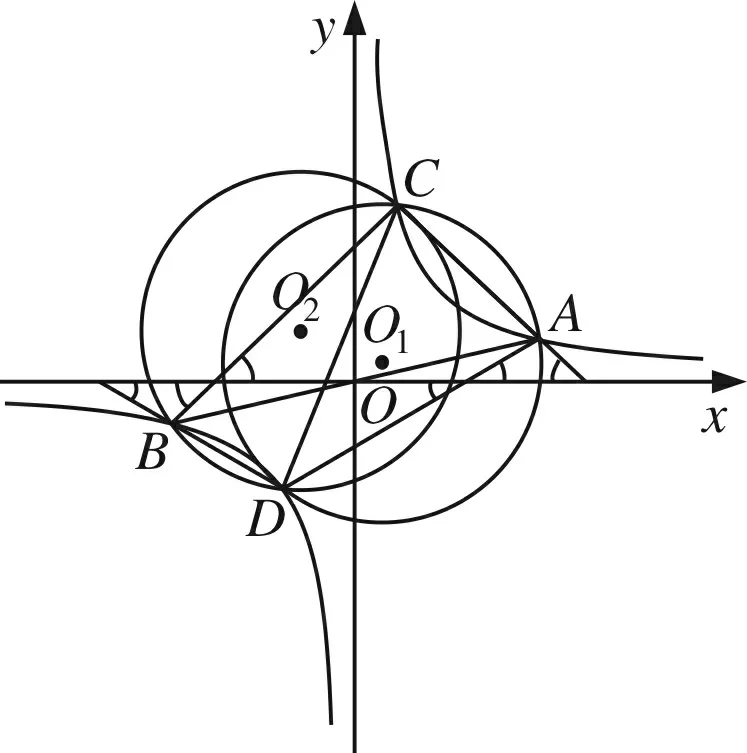
图6

例3解析如图6，延长CA交x轴于E，延长DB交x轴交于F，记AD、BC与x轴的交点为G、H.

由上述双曲线等角定理，可得∠CEH=∠CHE=∠BHF，∠DFG=∠DGF=∠AGE，所以∠CAD=∠CBD，又因为CD=CD，所以⊙O1和⊙O2是等圆.

结论得证.

由以上几例可以看出，“等角对等弦”，在非同等圆中大有作为，不可等闲视之.

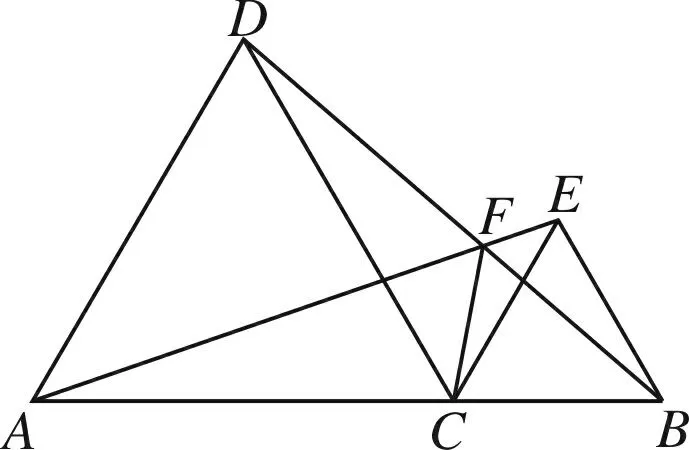
图7

还可以对这个定理再作进一步推广：

如果两圆的相似比为k，则两圆中相等的圆周角所对的弦之比也为k.

例4如图7，C是线段AB上一点，AC=2BC，以AC、BC为边，在AB的同侧作等边△ACD和等边△BCE，AE、BD交于F．若CF=3，DF=a，EF=b，则a、b满足( )

A.a=2bB.a=2b+1

C.a=2b+2 D.a=2b+3

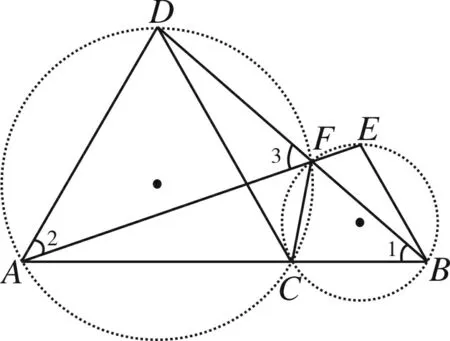
图8

简析这道题的背景非常熟悉.如图8，易证∠3=∠DAC=∠EBC=60°，所以A、C、F、D四点共圆，B、C、F、E四点共圆，且这两圆的相似比=AC∶BC=2∶1.

因为∠1+∠CAF=∠2+∠CAF=60°，

所以∠1=∠2(即两圆中的等角)，

所以DF=2CF，同理CF=2EF，

所以a=6，b=1.5，故选D.

用上述方法，可以解决如下问题，请你试一试：

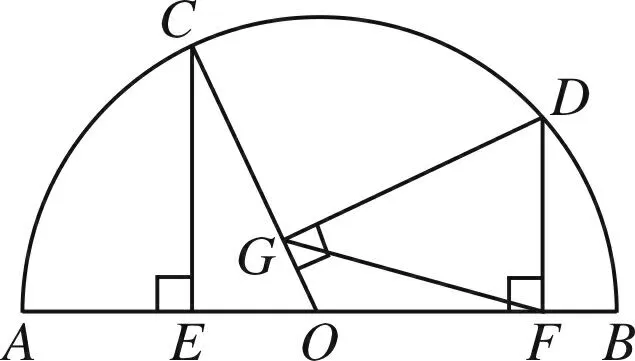
图9

如图9，半圆O的直径为AB，C、D是半圆O上的两点，CE⊥AB于E，DF⊥AB于F，DG⊥OC于G.试判断线段CE和GF的数量关系，并说明理由.