核心素养视域下中考试题命制的关注点
浙江省湖州市第五中学 (邮编:313000)
1 关注基本概念,注重数学理解
尊重教材,理解教材,以教材为依据设计试题.一可以充分发挥课本例习题的典型性、代表性和科学性的作用;二可以导引当今数学教学方向,是克服题海战术和极端功利主义的有效策略.通过教材或配套作业本中典型和具有代表性的例习题的直接引用、改编或引申而成的试题,让学生既熟悉又陌生,有效地与课本对接,考查对数学概念和数学本质的理解.

图1
例1如图1,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6 C.4 D.2
评注本题深入发掘课本中角平分线的性质定理,通过隐含条件“点P到BC的垂线段”这桥梁,添辅助线得到AP=PD,从而解决问题.很好地考查了学生对角平分线相关知识的理解、掌握和灵活运用的程度.

图2
例2如图2,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°. 过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
A.25° B.40° C.50° D.65°
评注本题深入发掘课本中切线的定义,90°的圆周角所对的弦是直径来解决问题,背景来源于课本,突出课堂教学引导学生经历概念形成过程和理解概念本质的重要性,对教学有很好的指导作用.
2 贴近生活实际,突出时代气息
以社会热点、旅游、农业、校园拓展类课程、社会养老问题为背景设计数学问题,考查知识点分别为图形的对称、科学计数法、反比例函数、统计、方程和函数建模思想等数学知识和方法解决实际生活问题.既充满时代气息,关注社会经济发展,又较好地反映了数学来源于生活又服务于生活的宗旨.
例3为了迎接杭州G20峰会,某校开展了设计“YJG20”图标的活动.下列图形中既是轴对称图形又是中心对称图形的是

评注本题以在杭州召开的杭州G20峰会为背景,考查了图形对称这一知识点,突出了时代气息,让学生在学习知识的同时也能关注时政热点.
例4随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位数不断增加.
(1)该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个.求该市这两年(从2013年底到2015年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三间(3个养老床位).因实际需要,单人间房间数在10至30之间(包括10和30), 且双人间的房间数是单人间的2倍.设规划建造单人间的房间数为t.
①若该养老中心建成后可提供养老床位200个,求t的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
评注本题随着社会老龄化日趋严重,养老问题已成社会重大民生问题之一.以湖州市养老机构的实际情况为背景,以及近几年湖州市每千名老人拥有的养老床位每年增长的情况命制.数据具有真实性和可靠性,考查了学生的阅读素养.通过对一元一次方程、一元二次方程、一次函数增减性等知识点和建模等思想方法解决实际问题的考查,意在检测学生阅读分析能力和解决问题的能力.
3 渗透PISA理念,关注数学本质
学以致用是学生学习的驱动力,只有学生真切感受到知识的应用价值,才能主动有效地学习.本题的取材内容贴近学生生活实际,使学生深刻感受到课堂上所学知识的实用性,体会到所学知识具有巨大的实际意义.

图3

图4
例5图3是我们常用的折叠式小刀.图4中刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成图4所示的∠1与∠2,则∠1与∠2的度数和是度.
评注试题蕴含着PISA理念:
一是含有“情境”,让每个学生都能参与到数学化过程中;二是关注运用,以学生熟悉的小刀片为背景,提炼出图形编制而成.
题中的“动中有静”,生活气息浓厚,但对知识点的考查又很简单.刀片转动中,∠1与∠2的度数和是一个定值.表面上此题仅仅考查了平行线的性质;实际上重点考查了数学的应用意识和解决问题的能力.并鼓励学生关注和热爱生活,善于利用数学思维来解决问题.


A.命题(1)与命题(2)都是真命题
B.命题(1)与命题(2)都是假命题
C.命题(1)是假命题,命题(2)是真命题
D.命题(1)是真命题,命题(2)是假命题
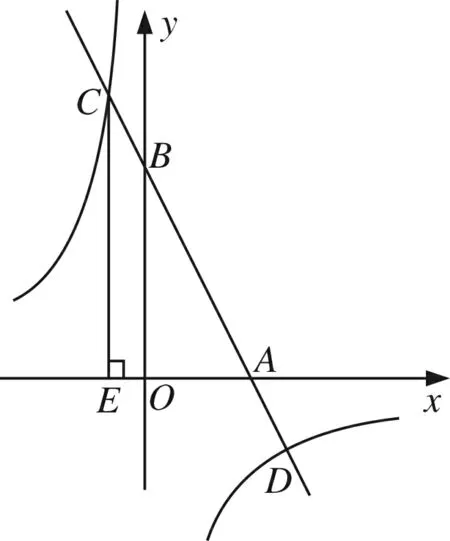
点评大家知道,数学的6个核心素养是:数学抽象、逻辑推理、数学建模、运算能力、直观想象、数据分析.本题通过阅读提炼和抽象出“派生函数”的定性性质:图象的对称轴在y轴的左侧和“派生函数”的定量性质:图象都经过同一点(0,0)是解决本问题的关键.试题难度不大,但却是考查学生核心素养的一种较好的尝试.
例7已知四个有理数a、b、x、y同时满足以下关系式:b>a,x+y=a+b,y-x 点评初看题目,认为四个有理数的大小比较应该不会困难,通过尝试发现试题内涵丰富,解法众多,是一道值得研究的好题. 动点问题年年有,我们翻看大多数的动点问题,一般都是点动牵引线动或点、线的动带动局部形状发生变化,下面的三类原创动点问题是通过折叠、平移、旋转的方法呈现的.目的是让考生通过“动中有静”的探究,关注数学学习的思想方法,凸显数学学习本质,试题的“动”较有特色. 图5 图6 图7 例8如图5,在等腰三角形ABC中,AB=AC=4,BC=7.如图6,在底边BC上取一点D,连结AD,使得∠DAC=∠ACD.如图7,将△ACD沿着AD所在直线折叠,使得点C落在点E处,连结BE,得到四边形ABED.则BE的长是 评注试题紧紧围绕着“四基”:基础知识,基本技能,基本思想方法,基本活动经验.主要考查了等腰三角形的性质,折叠的本质,平行四边形的性质,直角三角形勾股定理.如果注意观察,挖掘出隐含着圆,则容易证得AC∥BE,这对问题的求解是事半功倍的. 这类试题屡见不鲜,它既可以考查学生动手探索数学问题的能力,又能考查数学思维能力.该问题通过折叠这一熟悉的问题背景,将特殊三角形,平行四边形等相关知识有机地串联,让学生经历操作——观察——探究——计算的活动过程,在准确理解操作过程,分析操作结果获得数学知识.本问题是选取了这类折叠问题中的一个特殊位置来考查学生对折叠过程中图形本质的理解.在指导学生学习这类问题的解决策略的同时,还可以借助此类问题的背景,进行变式探究.例如: 变式一在等腰三角形ABC中,AB=AC=4,BC=7.在底边BC上取一点D,连结AD.将△ACD沿着AD所在直线折叠,使得点C落在点E处,使得△ACF为直角三角形.求CD的长. 图8 图9 变式二在等腰三角形ABC中,AB=AC=4,BC=7.在底边BC上取一点D,连结AD.将△ACD沿着AD所在直线折叠,使得点C落在点E处,使得△CDE为直角三角形.求CD的长. 图10 图11 变式三在等腰三角形ABC中,AB=AC=4,BC=7.在底边BC上取一点D,连结AD.将△ACD沿着AD所在直线折叠,使得点C落在点E处,使得△ACD是等腰三角形.求BE的长. 图12 图13 以上问题构成了一个问题串,通过这样一个问题串的研究,可以进一步探究发现,上述翻折问题的本质是一个点在圆上的运动的特殊位置.即以点E在点A为圆心,AC为圆心的圆上运动,以及∠CAE的角平分线AD之间所构成的位置和数量关系. 该题需要用动态的眼光分析,解决问题的灵活思维能力体现了新课程所倡导的动手实践自主探索的学习方式,同时该题在初中阶段学习的基础上,有意识地给学生今后的数学学习做了一个较好的准备和铺垫,有效地与立体几何在数学思维上进行了衔接,起到了桥梁延伸的作用.无独有偶,2016年浙江高考理科卷中第14题,实质上也是对这类折叠问题在空间上的探究,在初中阶段的平面范围内与高中数学空间范围内,两题呈现出“姐妹题”,是一次奇妙的高考题与中考题的偶遇,产生了遥相呼应的同频效果. 图14 变式四(2016年浙江理科高考题)在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是. 图15 例9已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上. (1)k的值是; 评注本题的动中有静是直线无论上下或左右平移,其中的待定系数k是不变的.本问题的设置较好地诠释了k的几何意义.通过设点P为(0,b),根据点P的平移,得到平移后的点为(-1,b+2)仍在直线y=kx+b上,可得:b+2=-k+b,从而求出k=-2.在这里很好地为考生的后续学习打下伏笔. 图16 图17 图18 例10数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究: 将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点). (1)初步尝试 如图16,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC; (2)类比发现 如图17,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH; (3)深入探究 总而言之,由于试题兼顾毕业与升学两重功能,因此数学的核心内容和主要思想方法是考查的重点,基础性和常规性是试题的主体.大部分试题来源于课本例习题和浙江省教研室编写的作业本改编而成的.试题从学科知识特点、学科思想方法和初高中衔接三个维度出发,加强对数学概念、数学本质、学习潜能和思想方法的考查.同时,重视渗透数学史、数学文化、PISA教育理念等.试题呈现形式多姿多彩,既要富有时代气息的正能量,又要蕴含丰富数学内涵创新思想.因此试卷的基础性、思想性、时代性、人文性、应用性、探究性、衔接性必须兼顾,试题设计必须:梯度明显、难度适中,目的使不同层次的考生发挥出自己的真实的水平.因此,中考复习要重视回归课本,关注思想方法,强化应用意识,突出发展能力.4 探究动态问题,感受数学之美