巧借“辅助圆”求解坐标系下全等问题——以两道坐标系下的三角形全等问题为例

浙江省绍兴市柯桥区平水镇中学 (邮编：312050)

初中几何中，在坐标系下由动点而产生的三角形全等问题历来是解题的难点，究其原因是由动点运动导致图形一直在变化，让学生难以分析出三角形全等时的位置，也无法从具体图形上分析求解.动点三角形全等问题的关键在于寻找确定的量，由这些定量探寻出动点形成的位置，从而根据位置分析出全等位置，即“由动寻定，由定定位，由位定点”. 虽有些试题，动点三角形全等直接跃然于纸上，让人一目了然；但有部分试题，动点三角形全等并非直观呈现，而是隐藏在所给的图形中，这就需要我们通过观察辨别和分析探究，合理地予以构造，借助“辅助圆”，化无序为有序、化“隐圆”为“显圆”，一针见血找到问题的本质，便能被有效快捷的解决.

1 知识预备

波利亚在《怎样解题》中指出“当我们的问题比较困难时，我们可能很有必要进一步把问题再分解成几部分，并研究其更细微的末节．”所以，研究几何图形，一个基本的方法就是要认真分析条件，寻找与之相关的基本图形，并利用这个基本图形的暗示作用来获得或推理相关的结论.

知识预备点1(静态条件下)：如图1，是4×4的正方形网络，方格纸中△ABC的3个顶点分别在小正方形的顶点(格点)上，这样的三角形叫格点三角形，如果以点D为另一个顶点作位置不同的格点△ABD，使所作的格点三角形与△ABC全等(不含△ABC)，那么，这样的格点三角形最多可以画出3个.

分析这种三角形全等构造属于“三定(点A、点B、点C)一动(点D)”．由于△ABC融于网格之中，直观、一目了然，所以易画出满足题意的三角形．笔者把图2称之为“镜面对称全等”型，图3称之为“角平分线全等”型，图4称之为“中心对称全等”型.

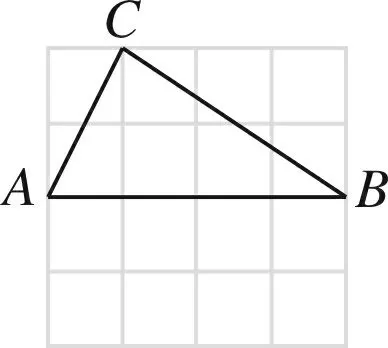
图1

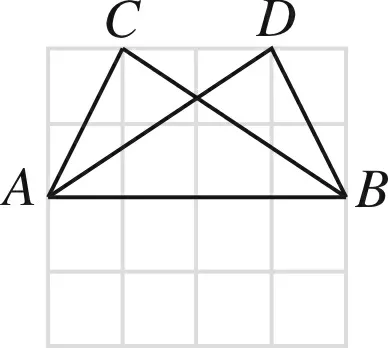
图2

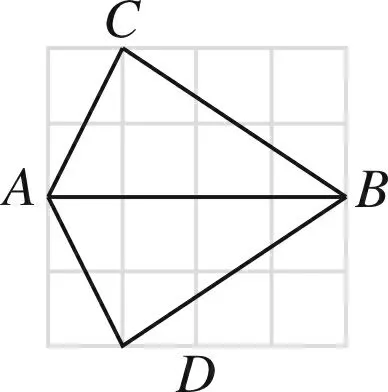
图3

图4

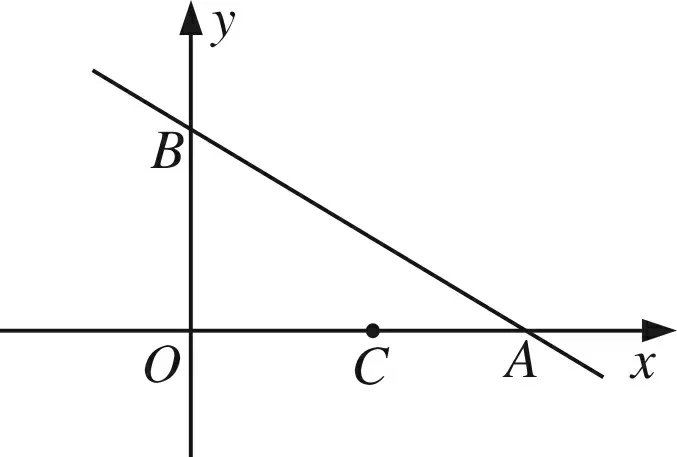
图5

图6

分析这种三角形全等构造属于“两定(点O、点C)两动(点P、点Q)”，显然难度比前者增大．由题意知，因为点C(4.8，0)，即OC是定长，所以△OQP中的点Q或点P必在以O为圆心，OC长为半径的圆上.这样要使以O、P、Q为顶点的三角形与△OCP全等，且这两个三角形在OP的异侧，则只存在两种情况:即OC=OQ或OC=PQ，但后者不满足题意，然后再作∠COQ的角平分线确定P点(如图6所示)．显然这种作图的思路是：先定圆，再定点，再作角平分线定另一个点，故把此方法称之为“3定全等” 型．这其实就是把图3的作图方式放在坐标系的背景下而已，而这种构图方式恰恰是解决一些坐标系下全等型问题的有效途径，需要学生在平时的学习中慢慢积累、体会，逐渐成为自己的解题利器.

2 典题举隅

例1(2018年嵊州市中考适应卷)定义：若四边形的一条对角线把它分成两个全等的三角形，则称这个四边形为等角四边形，并且称这条对角线为这个四边形的等分线．显然矩形是等角四边形，两条对角线都是它的等分线.

(1)如图网格中存在一个△ABC，请在图7，图8中分别找一个点D，并连结AD、BD，使得四边形ADBC是以AB为等分线的等角四边形．

图7

图8

图9

①求m的值.

②若点C的坐标为(5，0)，点P、点Q是△OAB边上的两个动点．当四边形OCPQ是以OP为等分线的等角四边形时，求BQ的长.

解析(1)此问其实属于“三定一动”型的全等构造，可参见图3、图4，图略.

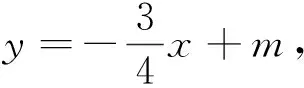
②此问属于“两定两动”型的全等构造，我们应分两种情况讨论：

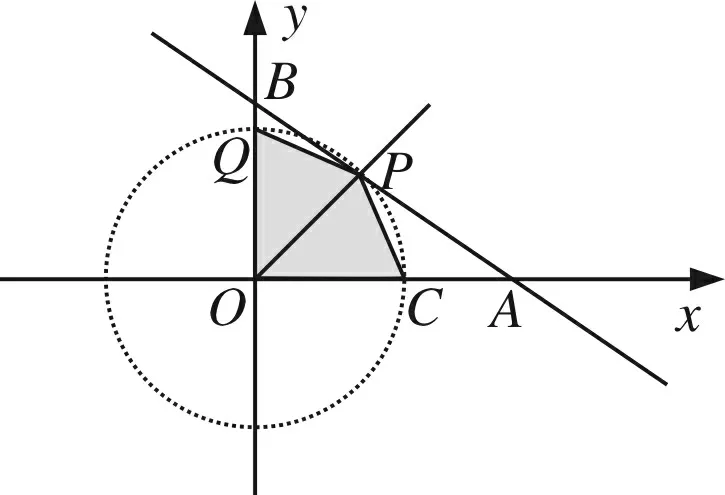
图10

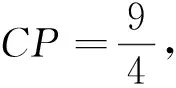
图11

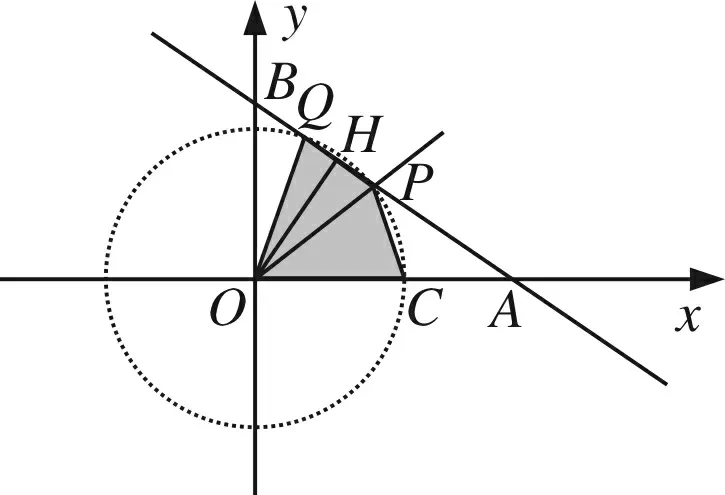
图12

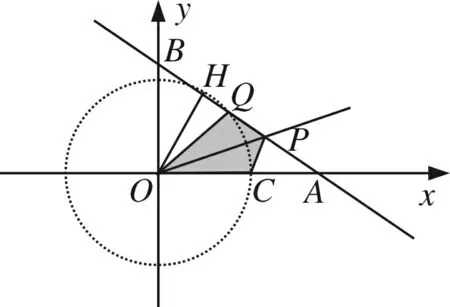
图13

当点P、Q两点都在AB上，有两种情形：由“3定全等”型的作图方法，画出如图12、图13的情形，显然四边形OCPQ都满足题意，此时过O作AB的高OH，则易求OH=4.8，BH=3.6，进而求得QH=1.4，所以在图12中的BQ=BH-QH=3.6-1.4=2.2，如图13中的BQ=BH+QH=3.6+1.4=5.

综上所知，满足题意的BQ长有BQ=1或BQ=3.75或BQ=2.2或BQ=5.

评注第(2)小题的第②问，关于“等角四边形”问题，根据约定，其实质是构造“三角形全等”问题．解答此题的关键是理解题意、领悟题意，再分层(点Q在OB上或点P、Q两点都在AB上)分类(再对每种情形尝试构图)，多面讨论，最终确定满足题意的图形．由此可见，借“图形”关联，明思维之道，用“模型”引路，逐步引导学生“由此向，及远方”．一旦悟透并掌握，这对于提高学生全面分析研究问题的能力大有裨益，真所谓“脑中有模型，心中有全等”，解法自然来.

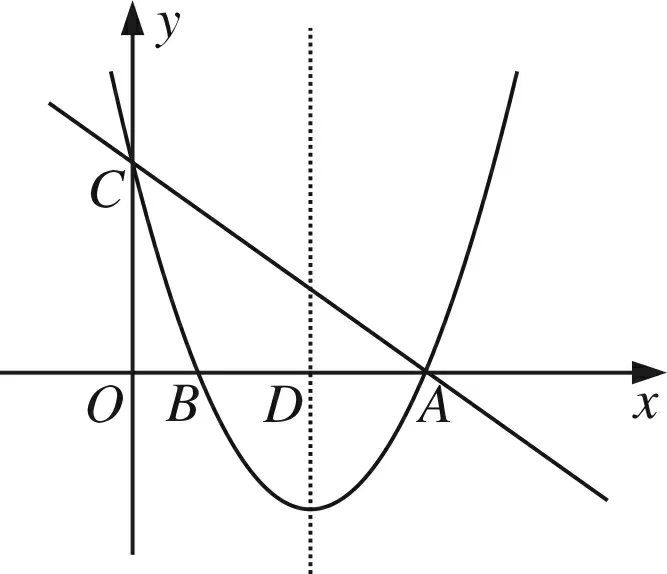
图14(1)

(1)求点A与点C的坐标；

(2)若在对称轴上有两个动点P、Q(点P在点Q的上方)，且PQ=2，求四边形BCQP周长的最小值；

(3)在△OCA的边上是否存在两点M、N，使得以M、N、O为顶点的三角形与△ODM全等？若存在，请求出M点的坐标；若不存在，请说明理由.

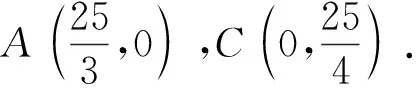
(2)略.

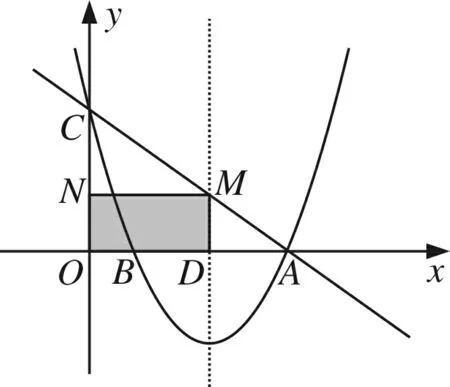
图14(2)

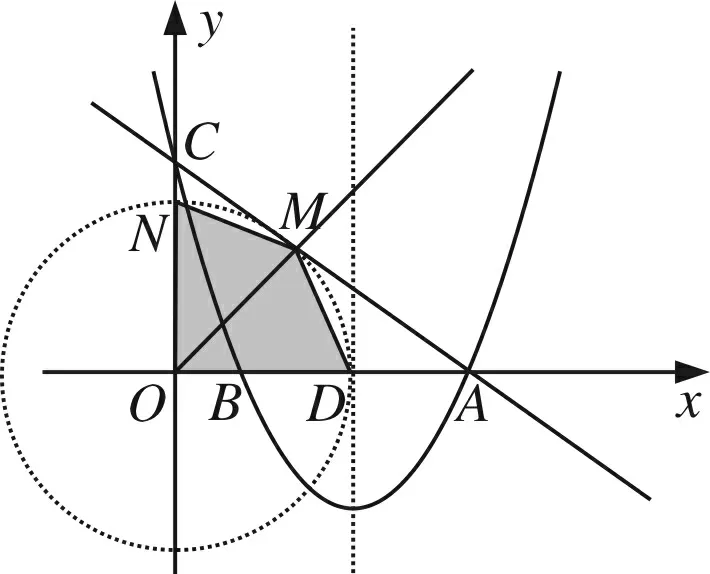
图15

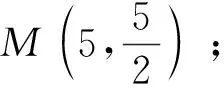
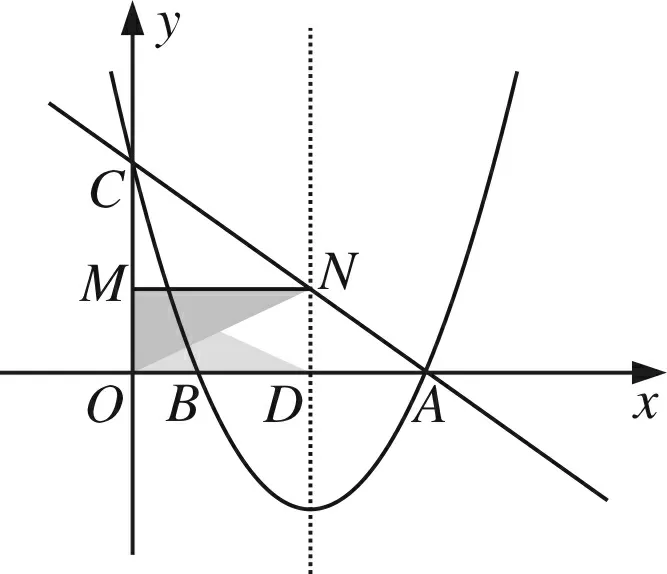
图16

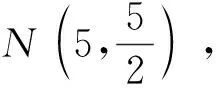
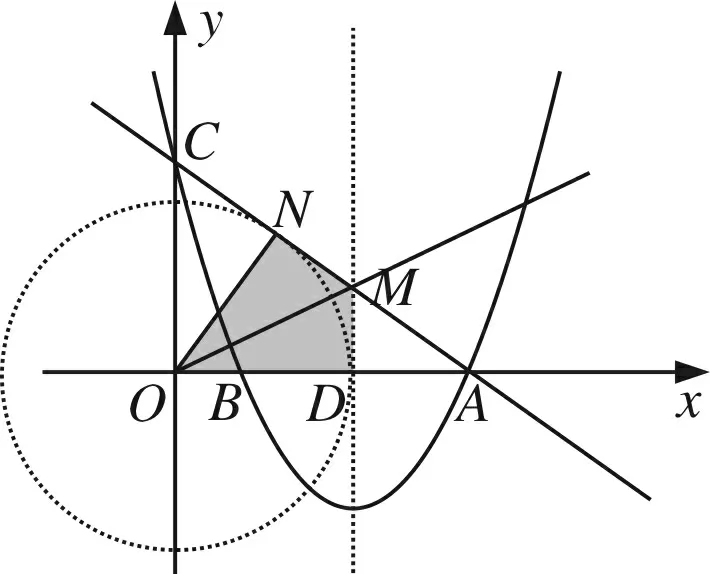
图17

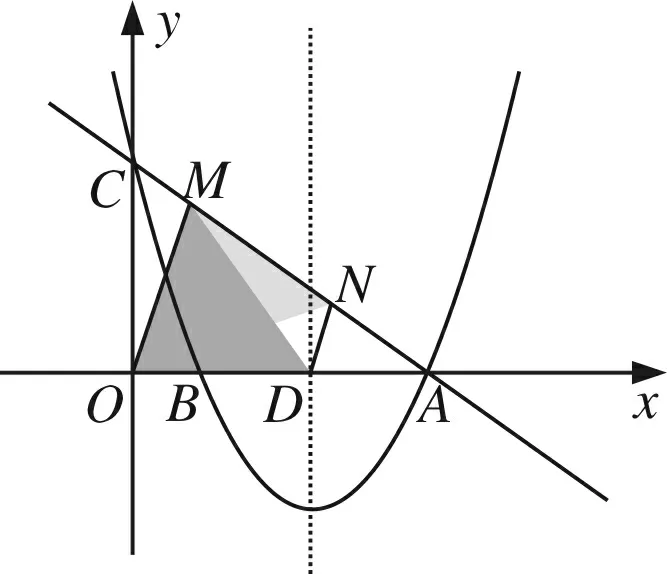
图18

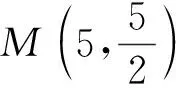
评注第(3)小题，关于构造“三角形全等”问题，解答除了需要经历观察、猜想、尝试等数学活动外，还要具备较深厚的构图功底．对于能分类探求出图14(1)—图17的情形已经不易，然后能构造出图18的情形，对学生来说实属不易，因为这一情形学生往往疏忽、遗漏．因此，如解决此类几何问题的一个基本策略就是：首先要认真审题，分析条件，将条件与相关“全等模型”结合起来，利用这个“全等模型”的性质，获得相应的结论．有时图形不一定有与条件匹配的“全等模型”，这是还需要联想相关知识作辅助圆构造出有效的“全等模型”，再通过众多信息的提取、组合，与已有模型关联、步步进阶，才能得心应手地将积累的知识及所提炼的方法应用创新，使思维敏捷，技法娴熟.

3 巩固提升

郑毓信教授曾说过：“知识求连，方法求变”.变则灵动，变则鲜活，变出智慧，变出情趣，“变”打开了学生获取解题方法的有效通道.进行有效试题“变式”可以链接中考试题或改编题，进一步感悟、理解问题的本质，数学思想方法，提升分析、思考、研究问题的思维能力.

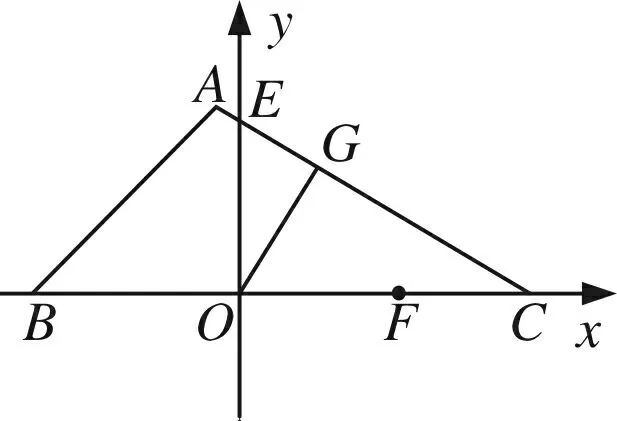
图19

(1)求AC所在直线的函数解析式；

(2)过点O作OG⊥AC，垂足为G，求△OEG的面积；

(3)已知点F(10，0)，在△ABC的边上取两点P、Q，是否存在以O、P、Q为顶点的三角形与△OFP全等，且这两个三角形在OP的异侧？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

通过上述例题的分析，我们不难看出：上述几种构造三角形全等的模型，单独来看，绝大部分中等偏上的同学已经掌握，可是在解题中隐藏着需要通过构造模型、构造辅助圆时，学生的分析能力和关联能力还是普遍欠缺，需要教师在平时的微专题复习中，开设相关的专题，重视对“问题串”的设计，设计一系列相互“关联”的、有“层次性”的“问题串”可以引导学生进行系统的、连续的思维活动；另一方面要重视对问题的变式探究，在比较、变化中体会问题的“形变而质不变”，进而促使学生能将掌握的知识、技能和模型意识应用到新问题解决过程中去，以提升学生的思维品质和综合能力.