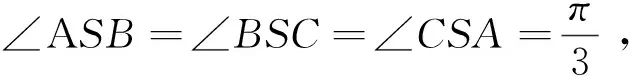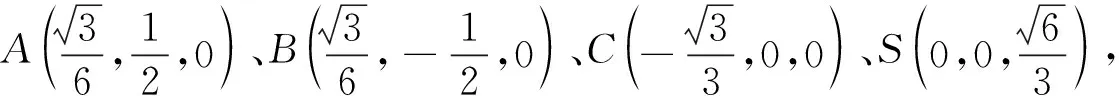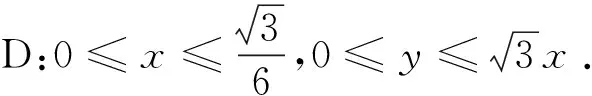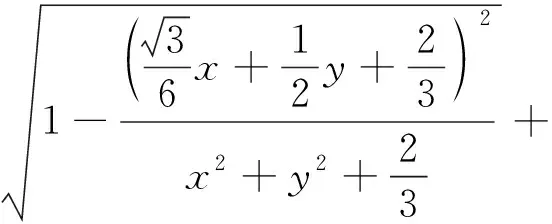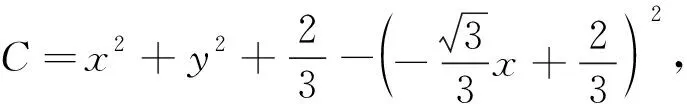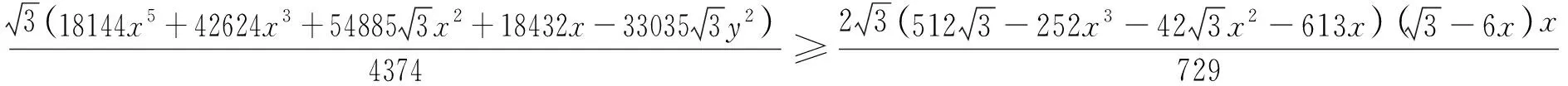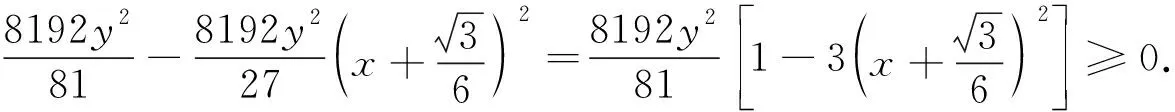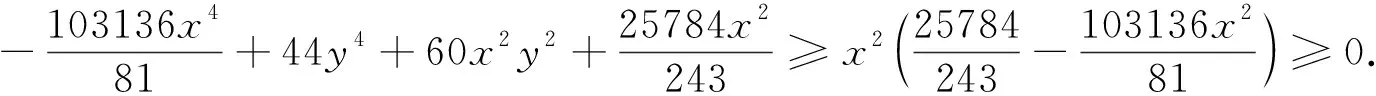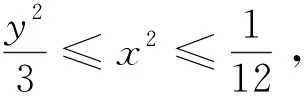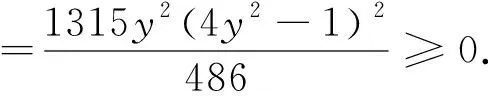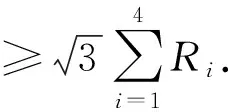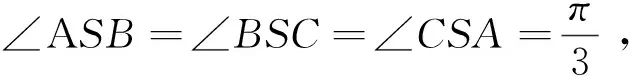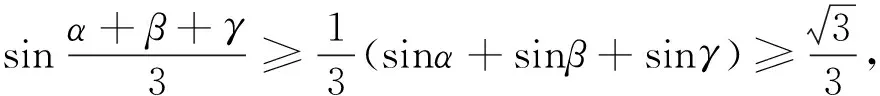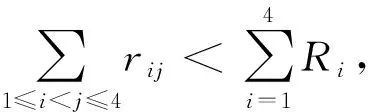关于四面体一个不等式猜想的证明

西安交通大学附属中学 (邮编：710054)

设rij是四面体A1A2A3A4内任意一点P到棱AiAj(1≤i

1997年，樊益武[1]证明了当P为四面体的重心时,有

①

2000年，唐立华[2]证明了当P为四面体的费马点时不等式①成立，同时猜想当P为四面体内任意一点时不等式①成立.2005年冷岗松在[3]中再次提到这个问题.

2017年，樊益武在[4]中提出了一个颠覆性猜想：

猜想设rij是正四面体A1A2A3A4内任意一点P到棱AiAj(1≤i

②

当且仅当P为正四面体A1A2A3A4中心或顶点时取等号.

本文将证明不等式②成立，从而否定了唐立华提出的猜想.为此我们需要以下引理.

③

根据△ABC的对称性，不等式③等价于

④

下面证明不等式④，为叙述方便记:

下面对以上五项作估值：

所以192ABCM-[(3M+C-A-B)2-4AB-12MC]2≥0.证毕.

不等式②的证明记∠PAiAj=αij(i≠j)，则

+R2(sinα21+sinα23+sinα24)

+R3(sinα31+sinα32+sinα44)

+R4(sinα41+sinα42+sinα43)

顺便指出，本文引理即为文[4]第17章《问题与猜想》的第一个猜想.由不等式③还可以证明文[4]中另一个猜想：

⑤

事实上，由于y=sinx在[0,π]上为凸函数，所以

最后值得一提的是关于此问题陈计曾猜测：设rij是四面体A1A2A3A4内任意一点P到棱AiAj(1≤i

据笔者所知，这个猜测还没有解决.