例说求异面直线所成角或角的三角函数值的方法

■胡景月

异面直线是空间中两条直线的位置关系的特殊情况,求异面直线所成角的关键是寻找异面直线所成角的平面角。下面举例分析求异面直线所成角的几种方法,供大家学习与参考。

一、勾股定理法

例1如图1,在正方体ABCD-A1B1C1D1中,M、N分别是CD、CC1的中点,则异面直线A1M与DN所成角的大小是( )。

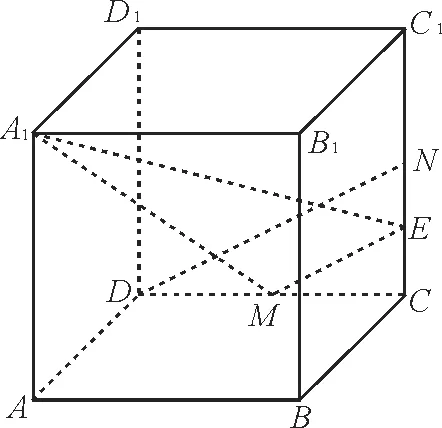
图1

A.30° B.45°

C.60° D.90°

解：设E为CN的中点。因为M是CD的中点,所以ME//DN,所以A1M与DN所成的角即为A1M与ME所成的角,即∠A1ME。令正方体的棱长为2,则A1M=3,。在△A1ME中,A1M2+ME2=A1E2,所以A1M⊥ME,所以∠A1ME=90°,所以异面直线A1M与DN所成角的大小是90°。应选D。

评注：利用勾股定理,既可以判断三角形是直角三角形,也可以作为直角三角形的性质进行应用。

二、余弦定理法

例2如图2,圆锥的底面直径AB=2,其侧面展开图为半圆,底面圆的弦AC=1,则异面直线AC与SB所成角的余弦值为____。

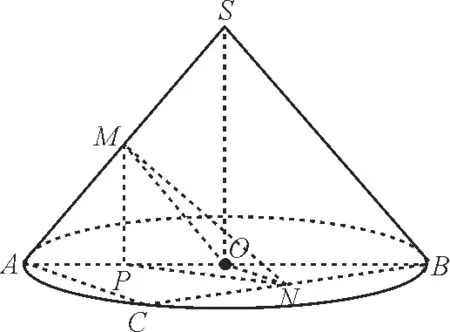
图2

评注：根据定义将异面直线所成的角转化为三角形中的一个角,再结合余弦定理求得结果。

三、三角函数定义法

例3在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60°,则异面直线PA与BC所成角的正切值等于____。

解：取AD的中点E,作PO⊥平面ABCD,如图3所示。

因为PE⊥AD,OE⊥AD,所以∠PEO为侧面与底面所成二面角的平面角,则∠PEO=60°。设AB=2,则EO=1,PE=2,AE=1。因为BC//AD,所以∠PAD为异面直线PA与BC所成的角。据此可得tan∠PAD=。

评注：根据定义将异面直线所成的角转化为直角三角形中的一个锐角,再结合三角函数的定义求得结果。

四、特殊点法

例4 如图4,在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,P是底面ABCD内(包括边界)的一个动点,若MP//平面A1BC1,则异面直线MP与A1C1所成角的取值范围是。

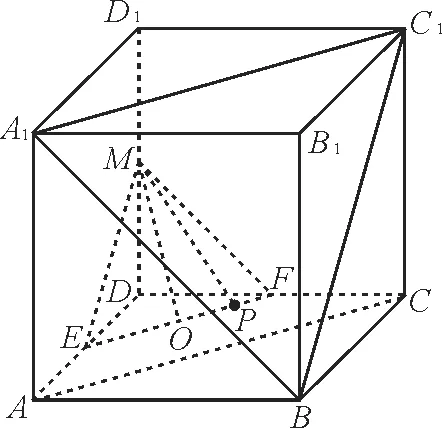
图4

解：取AD中点E,DC中点F,取EF的中点O。在正方体ABCD-A1B1C1D1中,M是棱DD1的 中 点,所 以ME//BC1,MF//A1B。因为ME⊄平面A1BC1,A1B,BC1⊂平面A1BC1,所以ME//平面A1BC1。同理可得MF//平面A1BC1。

因为ME∩MF=M,ME,MF是平面EFM内两相交直线,所以平面A1BC1//平面EFM。

因为P是底面ABCD内(包括边界)的一个动点,MP//平面A1BC1,所以P的轨迹是线段EF。因为ME=MF=EF,O是EF的中点,所以OM⊥EF。因为EF//A1C1,所以OM⊥A1C1,所以当P与O重合时,异面直线MP与A1C1所成的角取最大值

因为ME=MF=EF,P是EF上的动点,EF//A1C1,所以当P与E或F重合时,异面直线MP与A1C1所成的角取最小值。故异面直线MP与A1C1所成角的取值范围是。

评注：解题的关键是确定点P的轨迹是线段EF,当P与O重合时,异面直线MP与A1C1所成角取最大值,当P与E或F重合时,异面直线MP与A1C1所成角取最小值。

感悟与提高

如图5,在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成角的大小为_____。

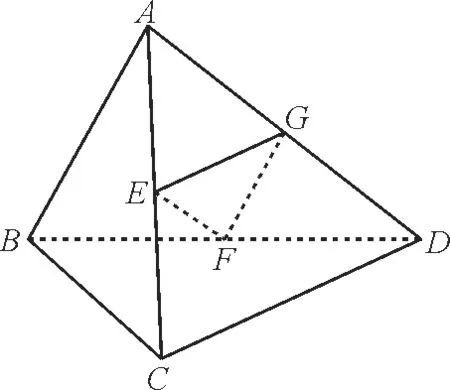
图5