2022 年高考“空间几何体”问题聚焦

■彭国强

下面以2022年高考题为载体,探究空间几何体问题的类型,以及求解的思维方法,希望对同学们的学习有所帮助。

聚焦1：旋转体的体积或表面积的计算

反思：理解旋转体的旋转过程,正确应用轴截面和侧面展开图中不变的量是解题的关键。本题主要考查运算能力、直观想象等数学素养。

聚焦2：多面体的外接球中的“直接法”和“函数法”

例2(1)(2022 年高考天津卷改编)已知正三棱台的高为1,上、下底边长分别为

反思：处理多面体的外接球问题的关键是确定球心的位置。求多面体的外接球的面积和体积问题的常用方法:①三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;②直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求出外接球的半径。

聚焦3：空间位置关系的判断

例3(2022年新高考卷)(多选题)如图1 所示,已知正方体ABCD-A1B1C1D1,则( )。

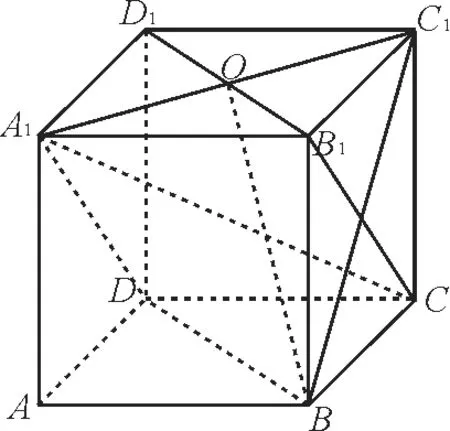
图1

A.直线BC1与DA1所成的角为90°

B.直线BC1与CA1所成的角为90°

C.直线BC1与平面BB1D1D所成的角为45°

D.直线BC1与平面ABCD所成的角为45°

解：因为DA1//B1C,所以直线BC1与B1C所成的角即为直线BC1与DA1所成的角。因为四边形BB1C1C为正方形,所以B1C⊥BC1,所以直线BC1与DA1所成的角为90°,A 正确。因为A1B1⊥平面BB1C1C,BC1⊂平面BB1C1C,所以A1B1⊥BC1。因为B1C⊥BC1,A1B1∩B1C=B1,所以BC1⊥平面A1B1C。又A1C⊂平面A1B1C,所以BC1⊥CA1,B正确。设A1C1∩B1D1=O,因为BB1⊥平 面A1B1C1D1,C1O⊂平 面A1B1C1D1,所 以C1O⊥B1B。因 为C1O⊥B1D1,B1D1∩B1B=B1,所 以C1O⊥平 面BB1D1D,所以∠C1BO为直线BC1与平面BB1D1D所成的角。设正方体棱长为1,则,所以直线BC1与平面BB1D1D所成的角为30°,C错误。因为C1C⊥平面ABCD,所以∠C1BC为直线BC1与平面ABCD所成的角。易得∠C1BC=45°,D 正确。应选ABD。

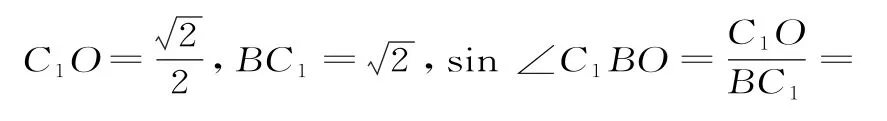
反思：以正方体模型为载体,考查空间位置关系问题是高考命题的热点,因此同学们一定要重视。

聚焦4：传统方法探究线线角、线面角以及二面角

例4(2022年高考浙江卷)如图2,已知正三棱柱ABC-A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点。记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F-BC-A的平面角为γ,则( )。

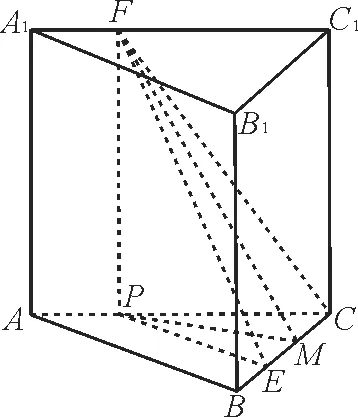
图2

A.α≤β≤γB.β≤α≤γ

C.β≤γ≤αD.α≤γ≤β

反思：传统方法作线线角、线面角、二面角的平面角的依据是利用定义得到的。利用直线的平行移动可作出异面直线所成的角;求斜线和平面所成角的关键是寻找斜线在平面上的射影的位置;二面角的平面角是在棱上找一点,在两个半平面内作与棱垂直的直线所成的角。