基于柱壳法及柱坐标系求解旋转体的体积

（信息工程大学 基础部，河南 郑州 450001）

在一元函数积分学中，微元法[1-3]是定积分的几何应用[4-5]和物理应用的理论基础.利用微元法可以求解旋转体的体积，但是当曲线围成的平面区域绕不同的坐标轴旋转时[6]，积分变量和体积微元的选取方式可能大相径庭，其中主要有柱片法和柱壳法2 种方式[7-8].在多元函数积分学中，也可以利用二重积分或三重积分求几何体的体积，对于旋转体而言，利用柱面坐标系[9-10]求解其体积计算过程非常简便.本文从利用定积分中的柱壳法求解旋转体的体积逐步过渡到利用三重积分在柱坐标系下计算旋转体的体积，将2种情形下求解旋转体的体积建立起联系，以达到学生对柱坐标系更容易接受和理解的目的.

1 柱壳法求解旋转体的体积

设函数y=f(x) ≥0,x=a,x=b及x轴围成的平面区域绕y轴旋转所得旋转体的体积为V（见图1）.

取x为积分变量，积分区间为[a,b]，任取小典型区间[x,x+dx]⊂[a,b]，相应于[x,x+dx]的窄曲边梯形绕y轴旋转所得立体的体积近似于以2πx为长，以f(x)为宽，以dx为高的长方体的体积，即体积元素为dV=2πxf(x)dx，将体积元素在[a,b]上作定积分，则得到旋转体的体积.柱壳法是求解此类型旋转体体积最常用的方法，其形式简单，计算起来方便快捷.

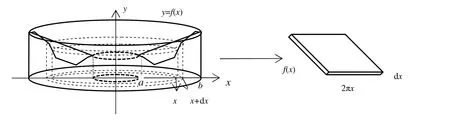
图1 利用柱壳法求解平面区域绕y 轴旋转得到的旋转体的体积

当y=f(x) ≥ 0且在[a,b]上单调减少时，可类似讨论.

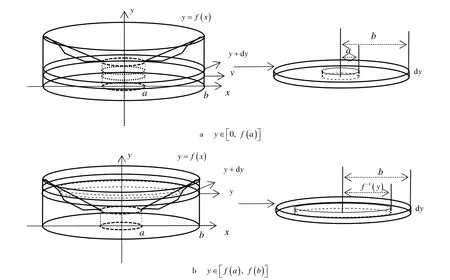
图2 当y =f (x) ≥ 0且在[a ,b ]上单调增加时，以y 为积分变量分割旋转体求其体积

讨论当y=f(x) ≥ 0，但不是[a,b]上的单调函数时的情形.由于y=f(x)在[a,b]上不单调，因此可以通过求y=f(x)在[a,b]上的单调性发生变化的点将区间[a,b]分成若干单调区间，分别求取每个单调区间所对应的曲边梯形绕y轴旋转所得立体的体积，求和即得总旋转体的体积.假设分点为x1,x2,L,xk-1，令x0=a,xk=b，若[xi,xi+1]是y=f(x)的单调增区间，由分析可知

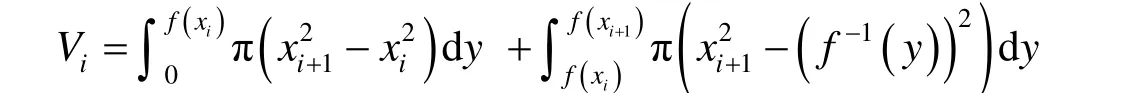
若[xi,xi+1]是y=f(x)的单调减区间，同理可得，因此整个旋转体的体积为.至此，以y为积分变量求解旋转体的体积问题便得到了解决.

至此，分别以x,y为积分变量，利用微元法解决了旋转体体积的求解问题.有的学生自然会想到能否以另一种方式对旋转体进行分割，即以过旋转轴的平面将旋转体分割成多个底面为扇环的曲顶柱体（见图3）.但遗憾的是，即使两张平面的夹角可以取很小，设为Δθ，此时由于x∈[a,b]，y=f(x)在[a,b]上的增量很大，不能找到一个体积微元来近似代替两张平面截旋转体所得的底面为扇环的曲顶柱体的体积.但如果继续分割，添加以旋转轴为轴的圆柱面和y为常数的水平面对此曲顶柱体进行分割，也即将3种分割方式结合在一起对旋转体分割，切割出来的小扇环柱体体积的近似值就是柱坐标系下的体积微元（见图4）.由此以平面极坐标中的极角为横坐标，极径为纵坐标，旋转轴为竖坐标建立柱坐标系.

图3 以旋转角θ 为积分变量对旋转体进行分割

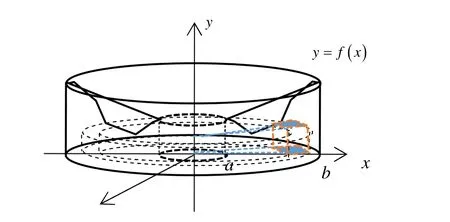
图4 以 r,θ,y为积分变量对旋转体进行分割

2 柱坐标系下求解旋转体的体积

在柱坐标系下，用3 组坐标面r=常数，θ=常数，y=常数分割旋转体，把旋转体分成若干个小立体，任取其中一个小立体，它的体积可近似看成以dr,rdθ,dy为长、宽、高的立方体的体积，因此旋转体的体积微元dv=rdrdθdy.曲线y=f(x)绕y轴旋转而成的旋转面方程为，在柱坐标系下也即是y=f(±r)，记旋转体所占空间区域为Ω，则利用直角坐标系下三重积分计算中的“先一后二”法可得旋转体的体积为.

在对旋转体的不同分割下如何求体积的思考中，引出了利用柱坐标求解旋转体体积的方法.随着问题的逐步推进，从柱壳法到柱坐标系，实现了一元函数定积分求解旋转体体积到重积分求解立体体积方法的跳跃，既解答了学生在定积分应用中求旋转体的体积时产生的疑问，又给了柱坐标系一个较为自然的引入.这种拓展有利于开阔学生的思维，帮助学生建立前后知识间的深层链接.