电磁驱动薄壁铝合金柱壳的动态膨胀变形特征

许永鹏，董新龙

(宁波大学机械工程与力学学院，宁波 315211)

0 引 言

薄壁金属柱壳结构的动态膨胀变形及其局域化演化、破坏、碎裂过程的研究在高速塑性成型领域具有重要意义。试验研究中，常采用内部爆炸、电磁驱动以及气炮压缩的方法使柱壳试样的内芯材料发生变形，实现均匀的膨胀变形及破坏。其中，利用螺形电磁线圈驱动金属薄壁柱壳高速膨胀的方法具有加载简单、易于控制、无机械作用引起的应力波传播等优点，在试验研究中应用广泛。1965年NIORDSON[1]最早提出电磁驱动金属膨胀环的高应变速率拉伸加载试验装置；随后，有学者采用电磁膨胀环技术研究了铝、铜等合金圆环在动态膨胀冲击载荷作用下的结构塑性响应行为及碎裂特性[2-4]；WESENBERG等[5]利用电磁线圈驱动金属薄壁圆管，分析了圆管的碎裂特征；还有学者利用电磁驱动Al6061-O铝合金圆管膨胀，探讨了应力状态对圆管变形的局域化演化及破坏的影响[6-9]；桂毓林等[10]和傅爱杰等[11]均利用电磁驱动铝合金膨胀，探讨了铝合金的失稳变形过程及其高速成型的“增塑性”机理；赵志衡等[12]采用有限元计算了电磁驱动管坯膨胀变形时的磁压力分布，发现放电瞬间径向磁压力在管坯上的分布不均匀，端部磁压力小于中部。目前的研究主要集中在电磁驱动金属柱壳动态膨胀变形的碎裂特征及其影响因素方面，关于动态膨胀过程中金属柱壳在不同轴向高度上的磁压力分布研究鲜有报道。

电磁驱动柱壳膨胀时，要求柱壳的动态膨胀变形均匀，以避免不均匀变形引起的柱壳失稳和碎裂。线圈和柱壳的结构会影响柱壳动态膨胀变形时的磁压力分布，从而影响变形的均匀性，因此，有必要对线圈和柱壳的结构进行合理设计，以满足均匀膨胀条件。作者采用ANSYS/Multiphysics多物理耦合场耦合有限元方法，对电磁线圈驱动铝合金圆管的膨胀过程进行了数值模拟，研究了螺形线圈高度固定时，不同轴向高度金属柱壳在线圈驱动下的磁压力分布和膨胀变形特性，为优化线圈和柱壳的结构参数提供参考。

1 试验方法及结果

1.1 试验方法

电磁驱动金属柱壳高速膨胀变形试验如图1所示：储能电容对螺形线圈放电产生瞬态磁场，根据洛伦兹原理金属环(管)会产生瞬态感应电流，感应电流产生的磁场与螺形线圈产生的磁场相互作用，驱动金属柱壳发生高速膨胀变形，最终发生破坏。试验分析中一般假设磁压力均匀分布在金属管壁上，膨胀变形为均匀膨胀。

图1 电磁驱动薄壁金属柱壳动态膨胀的试验原理示意图Fig.1 Diagram of experimental principle of dynamic expansion of electromagnetic driven thin walled metal cylindrical shell

试验薄壁柱壳材料为某厂家生产的薄壁6063-T6铝合金管，物理和力学性能见表1。柱壳外径为60 mm，壁厚为8 mm，轴向高度分别为20，30，40 mm；螺形线圈采用截面尺寸为3 mm×6 mm的紫铜线绕制，高度为32 mm，直径为58 mm，匝数为5匝，磁导率为1 H·m-1，电阻率为1.75×10-8Ω·m。将柱壳置于线圈外部，线圈与柱壳之间的间隙为1 mm。采用EMF50/18-V型电磁成型机加载，高压放电系统由4个300 μF的电容组成，最高放电电压为18 kV，最大储能为50 kJ。通过调整放电电压来改变柱壳的膨胀速度，试验时设置放电电压为7 kV。

表1 6063-T6铝合金的物理和力学性能Table 1 Physical and mechanical properties of 6063-T6aluminum alloy

1.2 试验结果

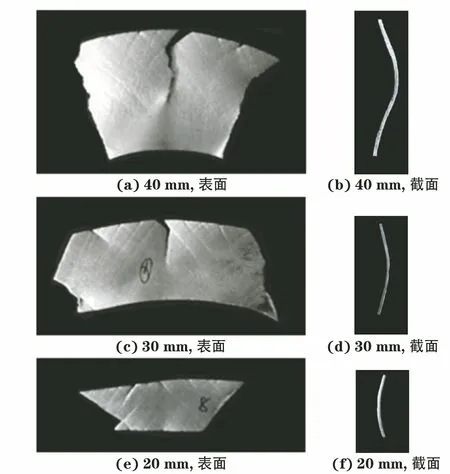
图2 不同轴向高度柱壳膨胀破坏后的表面和截面宏观形貌Fig.2 Surface and section macromorphology of cylindrical shell with different axial heights after expansion and failure: (a,c,e) surface and (b,d,f) section

由图2可以看出：当线圈高度为32 mm，柱壳轴向高度为20 mm时，柱壳发生外凹形的不均匀膨胀，说明端部的膨胀半径较中部的大；柱壳高度为30，40 mm时，柱壳发生内凸形不均匀膨胀，说明端部的膨胀半径小于中部的。当柱壳高度为40 mm时，柱壳表面可见清晰的集中变形的交叉滑移带，裂纹沿局域集中带扩展，柱壳发生不均匀的膨胀翘曲变形和碎裂，这说明该柱壳在动态膨胀时，发生了沿与径向成一定角度的剪切变形局域化集中。不均匀的膨胀翘曲变形会影响局域化集中、变形带的分布间距以及碎裂特征。轴向高度为20，30，40 mm的柱壳均发生了不均匀的膨胀变形，但高度为20 mm柱壳的变形较高度为30，40 mm的均匀，因此局域化带在柱壳表面的分布也更均匀。

2 有限元模拟及结果

2.1 有限元模型

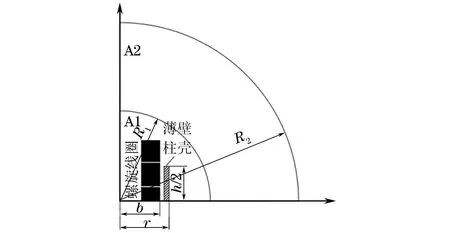
图3 柱壳电磁膨胀的1/4几何模型Fig.3 1/4 geometric model of cylindrical shell electromagnetic expansion

采用ANSYS/Multiphysics多物理耦合场耦合的有限元模型对螺形线圈驱动不同轴向高度柱壳的磁压力分布及膨胀变形情况进行模拟。柱壳与螺形线圈同轴放置，由于柱壳膨胀时磁场具有轴对称特性，为简化计算，取柱壳电磁膨胀的1/4几何模型进行分析。1/4几何模型如图3所示。其中：A1为近场空气区；A2为远场空气区；近场空气区边界半径R1为6h；无限边界半径R2为12h；空气磁导率为1 H·m-1;b为线圈半径;r为柱壳半径。有限元网格划分如图4所示，其中A1区采用Plane13三角形单元，A2区采用四边形四节点远场单元Infin110，螺形线圈和薄壁柱壳均采用Plane13平面四边形单元。有限元模型施加的边界条件如下：笛卡尔坐标系下，y=0时驱动线圈产生的磁感应强度与薄壁柱壳的对称平面垂直，x=0时磁场的矢量磁位为0；极坐标下，远场半径R取12h。假设电流在螺形线圈横截面上的分布均匀(不考虑电流集肤效应)，且不考虑涡流和温度对磁场分布的影响。

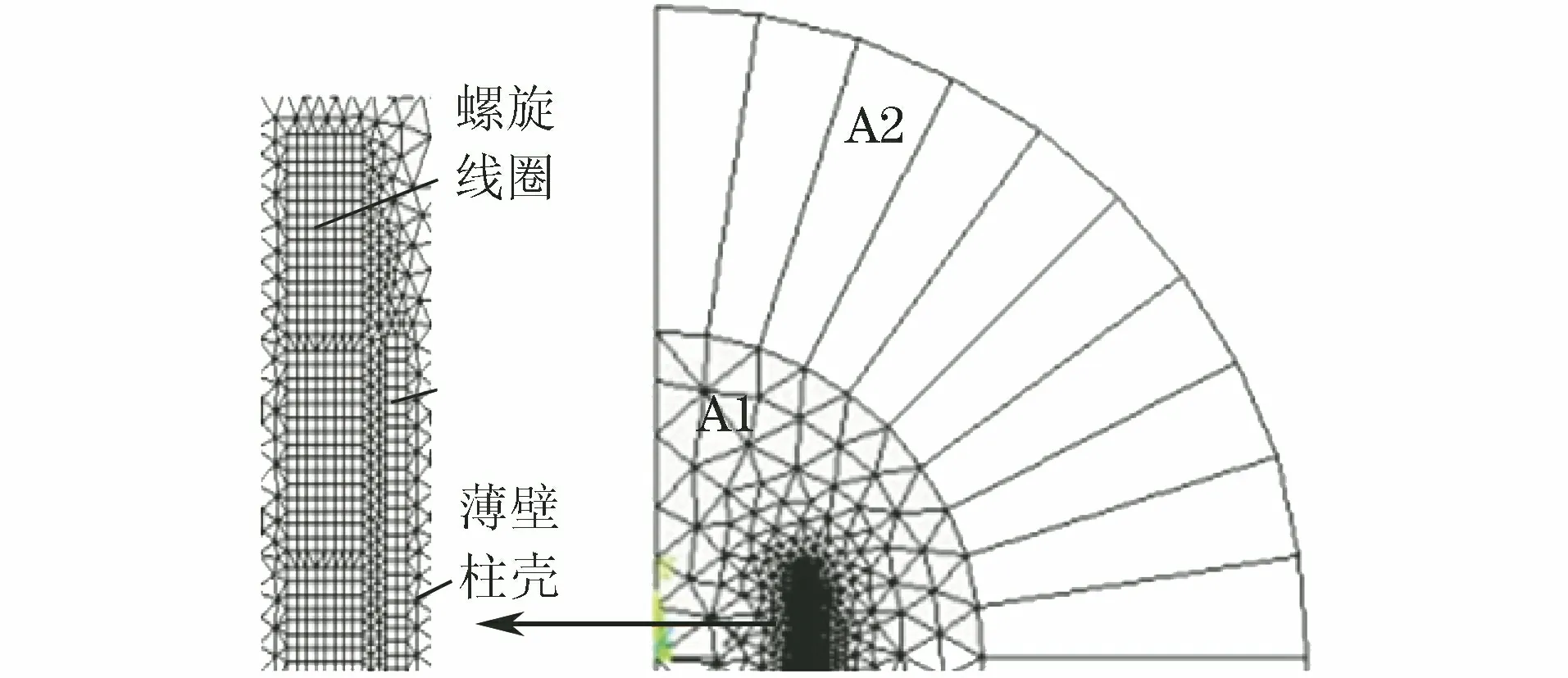
图4 柱壳电磁膨胀的有限元模型Fig.4 Finite element model of cylindrical shell electromagnetic expansion

有限元模型中，设置放电电压为7 kV，线圈高度为32 mm,柱壳高度分别为10,20,30,40 mm。对线圈施加的电流为

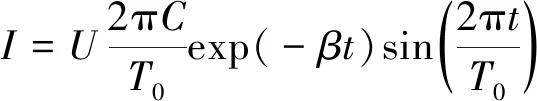
(1)

式中：C为储能系统电容；T0为放电电流周期；β为放电回路的衰减系数；t为放电时间；U为电容放电电压。

根据试验参数，C取300 mF，T0取0.001 8 s,β取3 600，U取7 kV。采用罗切斯特线圈测试得到线圈放电电流随放电时间的变化曲线见图5。

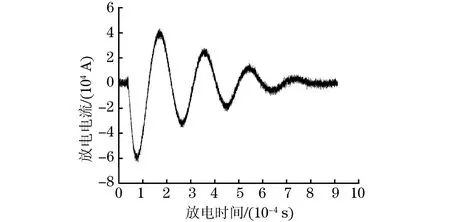
图5 线圈放电电流随放电时间的变化曲线Fig.5 Curve of coil discharge current vs discharge time

建模后用软件计算磁压力分布，将结果提交给结构场，分析柱壳结构在该磁压力分布下的变形情况，即采用第一个电磁场分析计算的结果，作为第二个结构场分析的载荷，将电磁和结构进行耦合，依次顺序迭代进行计算。

2.2 有限元模拟结果

由图6可以看出，线圈与柱壳之间狭小间隙内的磁力线与柱壳的高度方向平行，柱壳端部的磁力线发散，径向磁压力分布不均匀，除受径向磁压力外，柱壳还受轴向磁压力。

图6 轴向高度为20 mm柱壳的磁力线和磁压力分布Fig.6 Distribution of magnetic force lines (a) and magnetic pressure (b) of cylindrical shell with axial height of 20 mm

由图7可以看出：柱壳轴向高度为20 mm时，距端部5 mm处的径向磁压力与中部的相近；放电时间小于50 μs时，柱壳端部的径向磁压力明显大于中部的，放大时间长于50 μs时则相反。由于柱壳端部与中部的磁压力不同，柱壳会发生不均匀膨胀。由图8可以看出，随放电时间的延长，柱壳两端的径向膨胀量逐渐大于中部的，形成向外凹陷的翘曲变形。

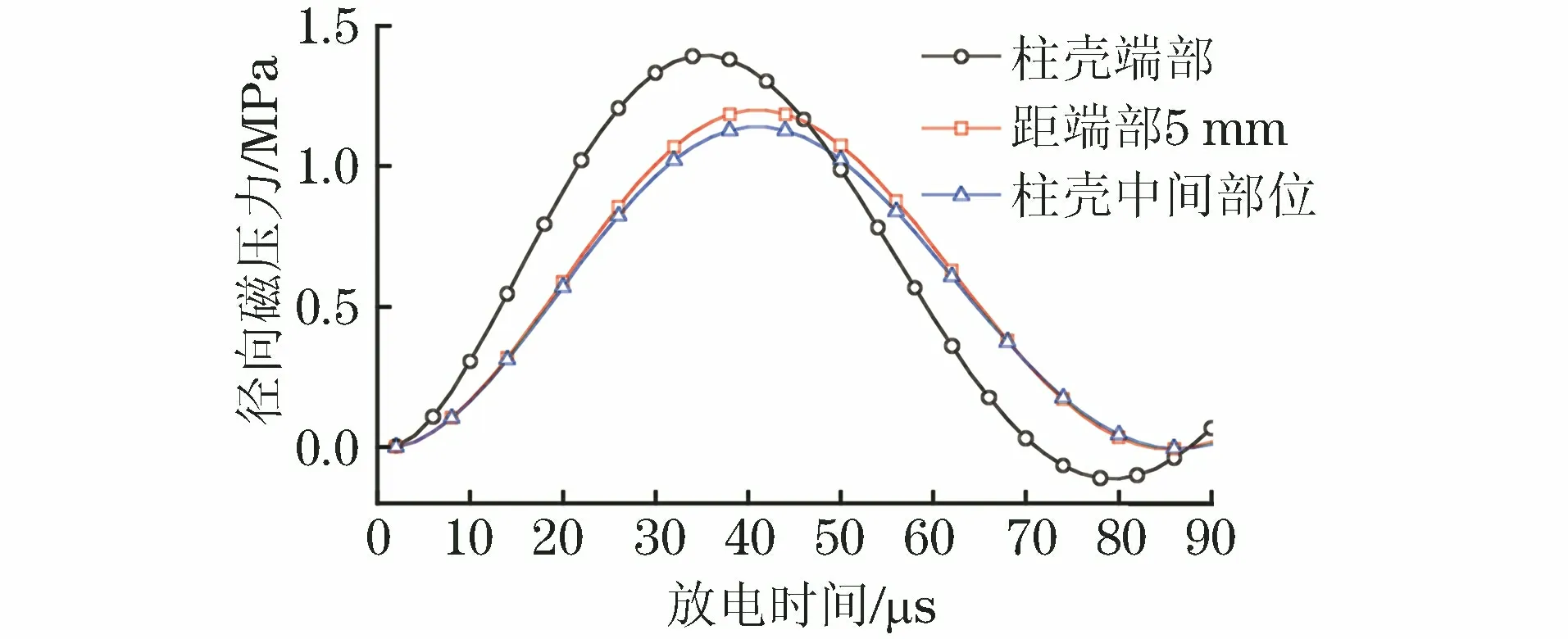
图7 轴向高度为20 mm柱壳不同位置的径向磁压力 随放电时间的变化曲线Fig.7 Curves of radial direction magnetic pressure vs discharge time at different positions of cylindrical shell with axial height of 20 mm

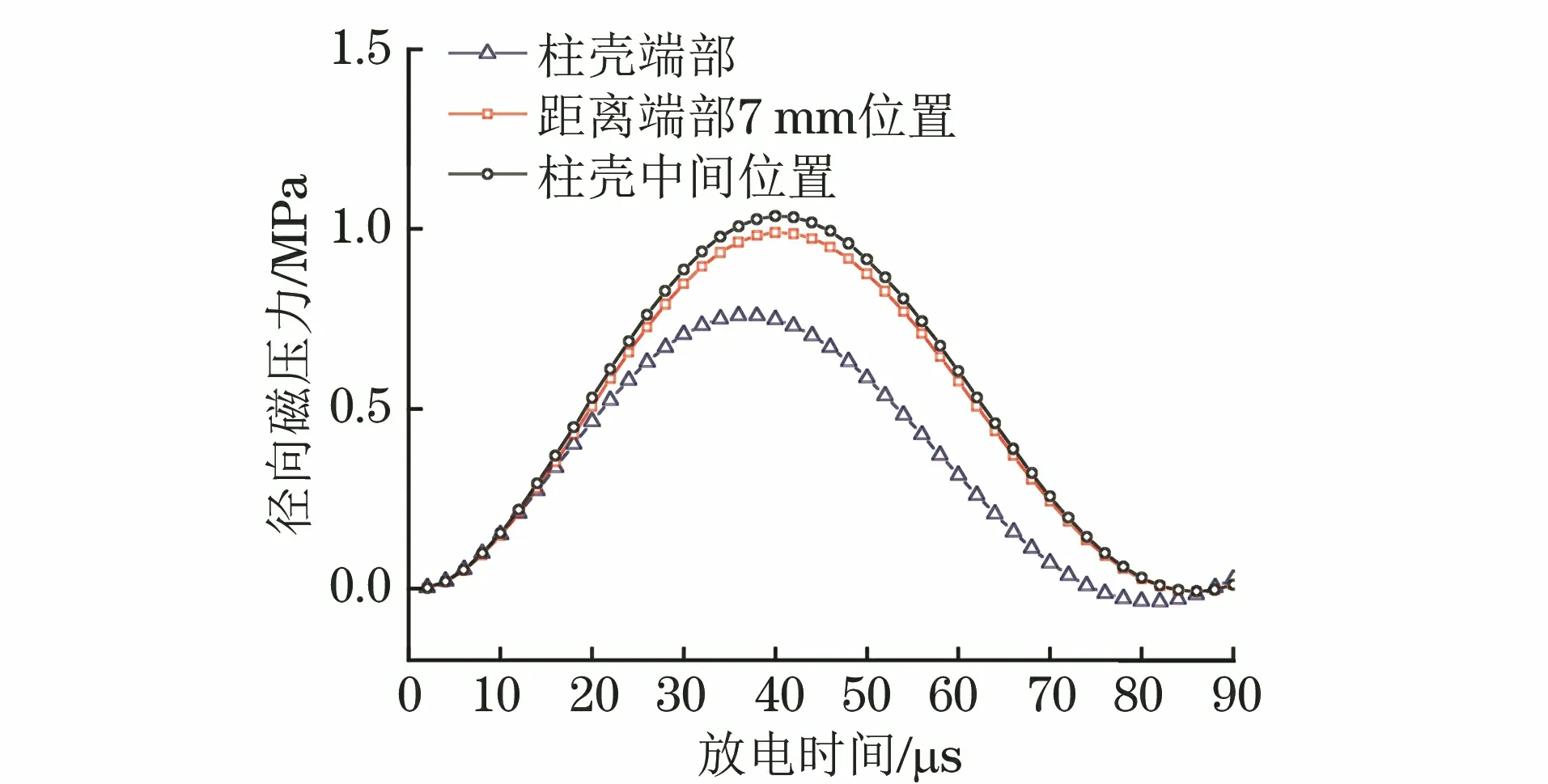
图9 轴向高度30 mm柱壳不同位置的径向磁压力随放电 时间的变化曲线Fig.9 Curves of radial direction magnetic pressure vs discharge time at different positions of cylindrical shell with axial height of 30 mm

由图9可以看出：轴向高度为30 mm时，柱壳中部的的径向磁压力和距离端部7 mm位置的相近，且大于端部的；放电电流在峰值(t=40 ms)附近时，中部的径向磁压力和端部的差值最大。说明轴向高度为30 mm时，柱壳的变形也不均匀。

由图10和图11可以看出：当线圈高度不变，为32 mm，柱壳高度为10，20 mm时，两端的径向磁压力大于中部的，柱壳高度为30，40 mm时则相反；不同高度柱壳中部的轴向磁压力均为0，说明中部不发生轴向变形。磁压力越大，膨胀越大，可见柱壳高度为10，20 mm时两端的膨胀较中部的大，高度为30，40 mm时，两端的膨胀小于中部的，与试验结果相符，说明模拟结果准确。

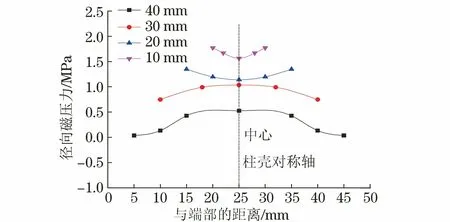
图10 不同轴向高度柱壳在放电电流达到 峰值时的径向磁压力分布曲线Fig.10 Distribution curves of radial direction magnetic pressure of cylindrical shell with different axial height when discharge current reached peak value

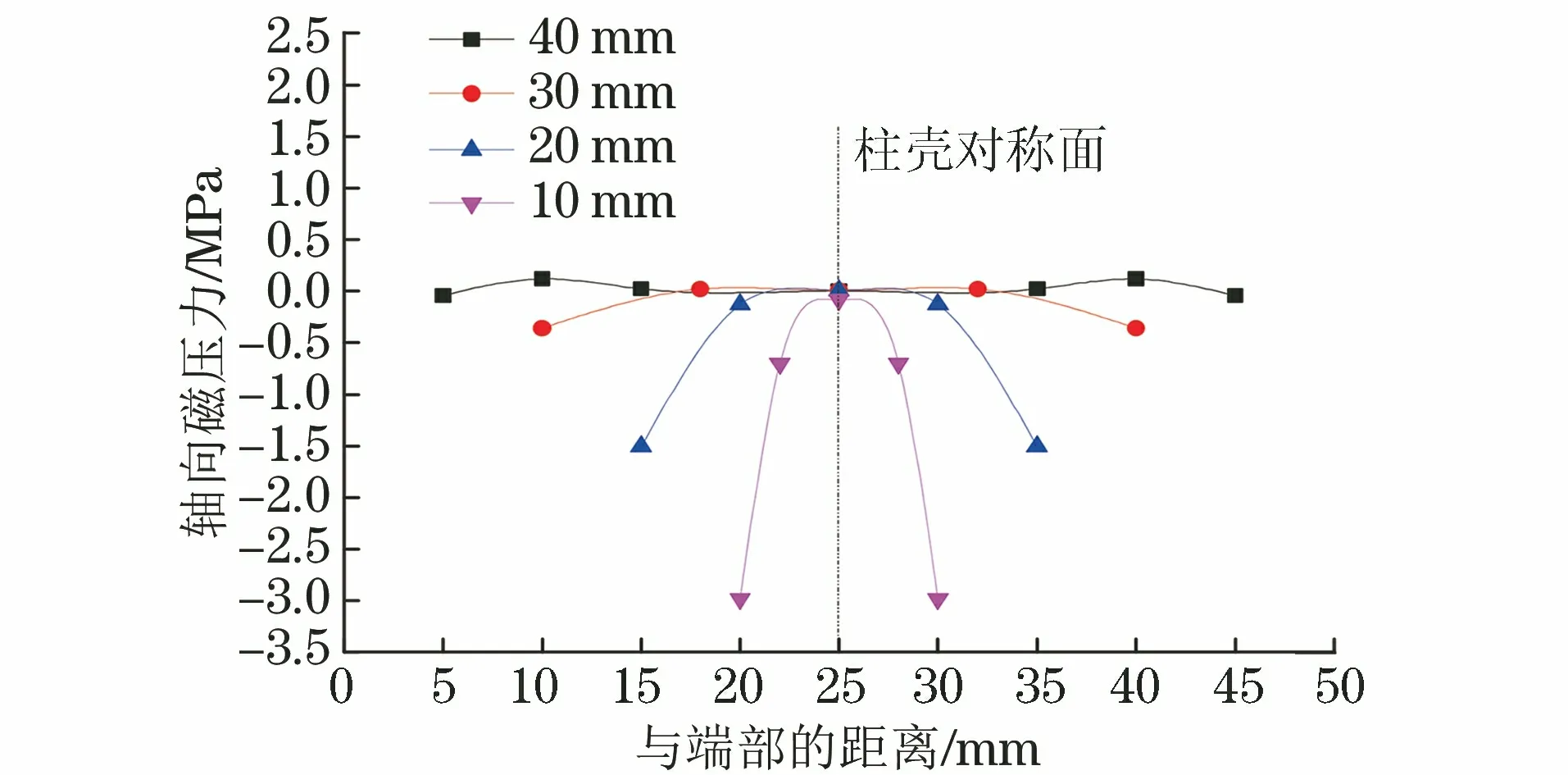
图11 7 kV放电电压下，不同轴向高度柱壳在放电电流达到 峰值时的轴向磁压力分布曲线Fig.11 Distribution curves of axial direction magnetic pressure of cylindrical shell with different axial heights when discharge current reached peak value under 7 kV discharge voltage

综上，不同轴向高度柱壳的径向磁压力分布及膨胀变形情况不同。对于给定高度线圈，随柱壳轴向高度增大，柱壳两端的径向磁压力从大于逐渐变为小于中部的，因此必然存在某一高度柱壳的径向磁压力在不同位置的分布均匀。将放电电流达到峰值时，不同轴向高度柱壳端部和中部的径向磁压力分布的不均匀性定义为

(2)

式中：f为磁压力分布的不均匀性；Pr(end)和Pr(mid)分别为端部和中部的径向磁压力。

由图12可以看出：柱壳与线圈的高度之比在0.7左右时，端部与中部的径向磁压力近似相等，此时磁压力分布均匀。

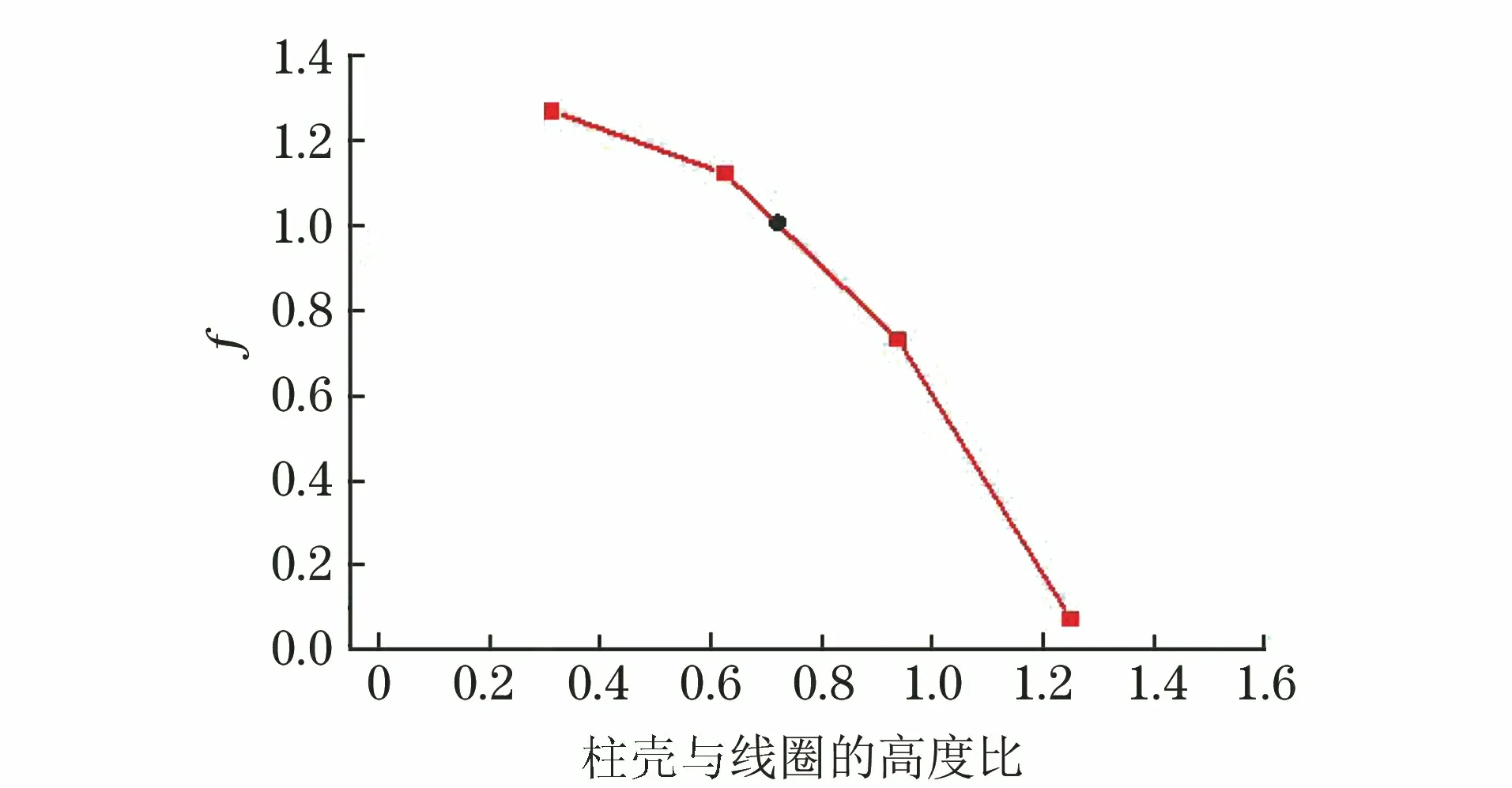
图12 径向磁压力分布的不均匀性随柱壳与线圈的高度 之比的变化曲线Fig.12 Curves of non-uniformity of radial direction magnetic pressure vs height ratio of cylindrical shell and coil

4 结 论

(1) 有限元模型能较准确地模拟电磁线圈驱动柱壳膨胀的径向磁压力分布和变形情况；放电电流达到峰值，柱壳高度为20 mm时，端部的径向磁压力大于中部的，发生外凹形不均匀膨胀，柱壳高度为30，40 mm时，径向磁压力小于中部的，发生内凸形不均匀膨胀。

(2) 柱壳与线圈的高度之比在0.7左右时，端部与中部的径向磁压力基本相同，此时径向磁压力分布均匀。