环氧树脂灌封结构热力耦合特性研究

张国亮，李悦芳，李 想

(中国工程物理研究院电子工程研究所，绵阳 621999)

0 引 言

环氧树脂灌封材料具有优异的高压绝缘性能、耐化学腐蚀性能和热力学性能，同时还具有低固化收缩率的特点。低固化收缩率这一特性有效减小了环氧树脂灌封材料固化过程中的力学载荷响应，从而能防止外载荷对灌封材料的损伤[1-2]。环氧树脂灌封材料涉及两种与温度相关的应力，一种为环氧树脂灌封材料在固化过程中产生的残余应力，另一种为完全固化后在温度载荷下产生的热应力。温度载荷是影响环氧树脂灌封材料应力分布的敏感因素，温度变化会使材料内部产生热应力[3-4]。因此，环氧树脂灌封结构涉及两种与温度相关的应力模型，一种为固化残余应力模型，另一种为热应力模型，这2种模型组成灌封结构的热力耦合模型。

目前，已有大量关于环氧树脂灌封材料在固化过程中产生的残余应力的研究报道[5-8]，而关于灌封材料的热力耦合特性鲜有报道。常用的环氧树脂灌封材料主要由双酚A环氧、改性剂和固化剂组成，室温时将三者混合均匀，在高温下加热，经固化后冷却至室温，得到固化后的环氧树脂灌封材料[9-11]。

作者通过不同温度下的拉力试验获取环氧树脂灌封材料的温变力学和物性参数，测试环氧树脂灌封材料的固化残余应变，再通过在线监测得到环氧树脂灌封结构在温度载荷下的热应变，最后以环氧树脂灌封材料的温变力学和物性参数以及固化残余应变作为输入条件，获取环氧树脂灌封结构在温度载荷下的应变和应力仿真数据。作者以60 ℃固化温度下的环氧树脂灌封材料为研究对象，分析了环氧树脂灌封结构的热力耦合特性，为其他固化温度下的环氧树脂灌封结构的热力耦合特性的研究提供参考。

1 热力耦合模型

1.1 固化残余应力模型

JOHNSTON等[5-6]提出了与环氧树脂固化度和固化温度相关的瞬时模量物性参数本构模型，在此基础上，SVANBERG等[7-8]通过分析线性黏弹性本构模型的极限情况得到与路径相关的环氧树脂灌封材料的黏弹性固化残余应力模型。相对于线弹性模型，黏弹性模型具有两个优势：一方面，该模型可以较好地反映固化过程中树脂的性能变化；另一方面，在不明显降低计算精度的前提下，该模型能有效地预测环氧树脂灌封材料的固化变形和残余应力。因此，该模型在工程上得到了广泛的应用。

环氧树脂灌封材料的瞬时模量本构方程为

(1)

T*=(Tg(0)+aTgX)-Tg(t)

(2)

式中：X为环氧树脂固化度；Er为与固化度有关的模量；Er(0)为固化度为0时的模量；Er(∞)为固化度为1时的模量，Er(∞)=1 000Er(0)；Tc1为环氧树脂模量变化的下限温度；Tc2为环氧树脂模量变化的上限温度；Tg(0)为环氧树脂未固化时的玻璃化转变温度；Tg(t)为瞬时玻璃化转变温度；aTg为环氧树脂玻璃化转变温度模型常数。

黏弹性固化残余应力本构方程为

(3)

式中：Cijkl(r)为环氧树脂橡胶态的模量张量；Cijkl(g)为环氧树脂玻璃态的模量张量；εkl为环氧树脂的总应变张量；εkl(E)为环氧树脂体积变化产生的应变张量(包括环氧树脂热应变、化学收缩应变)；tvit为环氧树脂橡胶态向玻璃态转变的最后时刻；Tg(X)为与环氧树脂固化度相关的玻璃化转变温度，其与固化度的关系为

(4)

式中：Tg(∞)为环氧树脂固化度为1时的玻璃化转变温度；λ为环氧树脂材料常数。

1.2 热应力模型

热弹塑性力学本构模型基于弹塑性力学本构模型，考虑了温度变化产生的热膨胀对结构的影响，其基本控制方程包括热应力广义虎克定律、力学位移和力学变形连续方程[12-13]，热应力广义虎克定律表达式为

(5)

(6)

式中：εxi为主应变;σxi为主应力;νxixj为剪应变；τxixj为剪应力；Θ=∑σxi,为体积应力；ΔT为温度差;α为热膨胀系数；G为剪切模量；ν为泊松比。

力学位移方程为

(7)

式中：e=∑εxi，为体积应变;ui为位移；2为拉普拉斯算子；Xi为单位体积力在坐标轴xi上的分量；λ1为常数;β为热应力系数。

力学变形连续方程为

(8)

(9)

2 试样制备与试验方法

根据GB/T 2567-2008，制备了由双酚A环氧、改性剂和固化剂组成的环氧树脂灌封材料，固化温度为60 ℃。

采用动态力学分析法(DMA)测定环氧树脂灌封材料的玻璃化转变温度，采样频率1 Hz，升温速率1 ℃·min-1，温度范围-40～80 ℃。采用A1-7000-M1型万能拉力试验机与温度箱组合设备测试环氧树脂灌封材料随温度变化的力学参数，试样尺寸如图1所示。测试时，在试样中间粘贴电阻应变片。拉伸速度为2 mm·min-1，温度箱的温变速率为1 ℃·min-1，环境温度范围为-30～60 ℃，记录每个温度条件下的弹性应变，以计算随温度变化的弹性模量和泊松比。采用Q400型热机械分析仪测定环氧树脂灌封材料的热膨胀系数，升温速率为1 ℃·min-1，环境温度范围为-30～60 ℃。

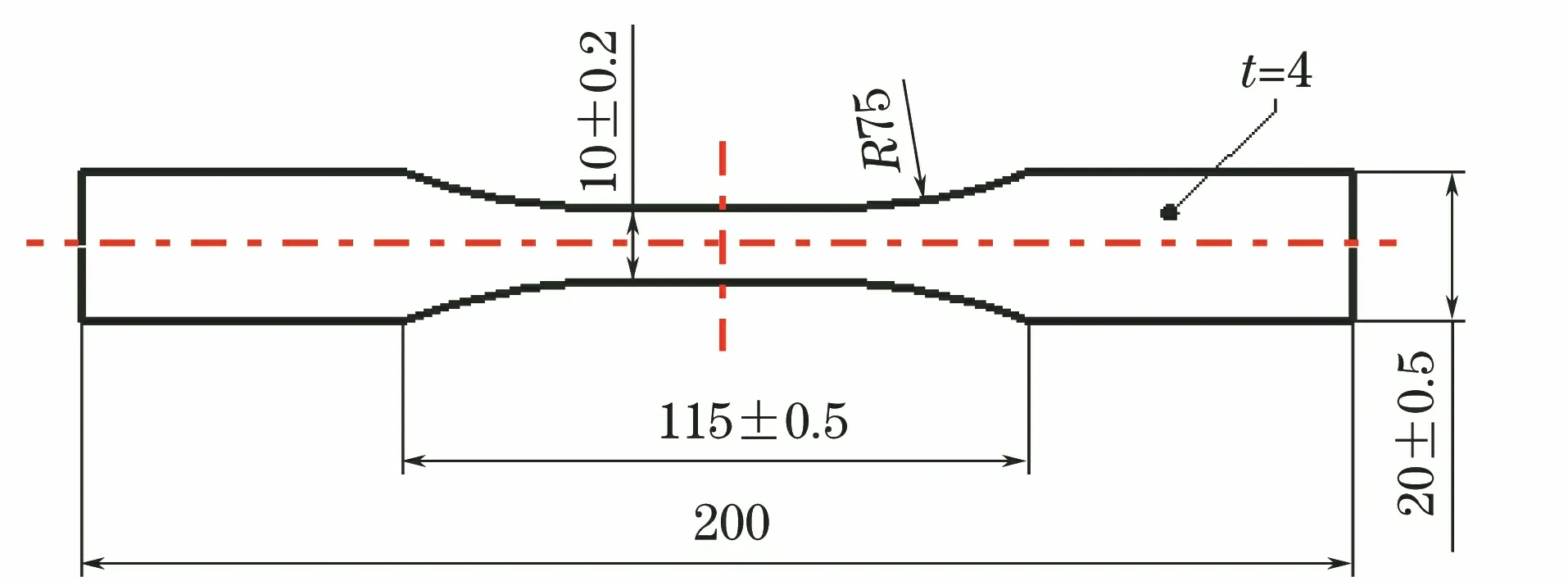
图1 环氧树脂灌封材料力学参数测试试样尺寸Fig.1 Dimension of sample used in mechanical parameter testing of epoxy resin potting material

采用4个均匀分布的电阻应变片(间隔角度为90°)测试环氧树脂灌封材料固化结束后的残余应变，试样尺寸如图2所示。薄壁(壁厚1 mm)金属筒和金属杆均为可伐合金，金属杆用于定位金属筒在灌封材料中的相对位置，电阻应变片提前布置于金属筒内壁。通过电阻应变片测试环氧树脂灌封材料固化过程中的残余应变。电阻应变片的阻值为120 Ω，最高工作频率为1 kHz。

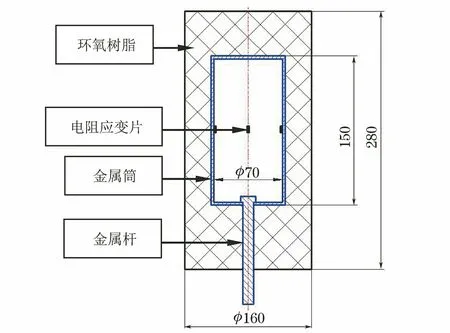
图2 残余应变测试试样尺寸Fig.2 Dimension of sample for residual strain test

环氧树脂灌封材料固化成型后，在环氧树脂灌封结构试样外表面粘贴3个电阻应变片，分别位于上部、中部和下部，测试灌封结构在环境温度下的热应变，如图3所示。电阻应变片阻值为120 Ω，最高工作频率为1 kHz。试验环境温度条件如图4所示，温变速率为1 ℃·min-1。

图3 热应变测试试样Fig.3 Sample for thermal strain test

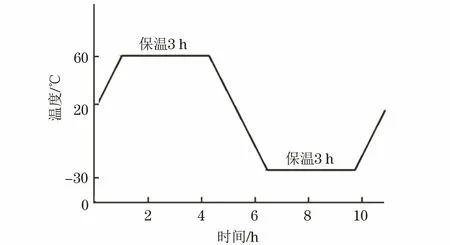
图4 热应变测试的环境温度条件Fig.4 Environment temperature conditions for thermal strain test

3 试验结果

3.1环氧树脂灌封材料的力学和物性参数

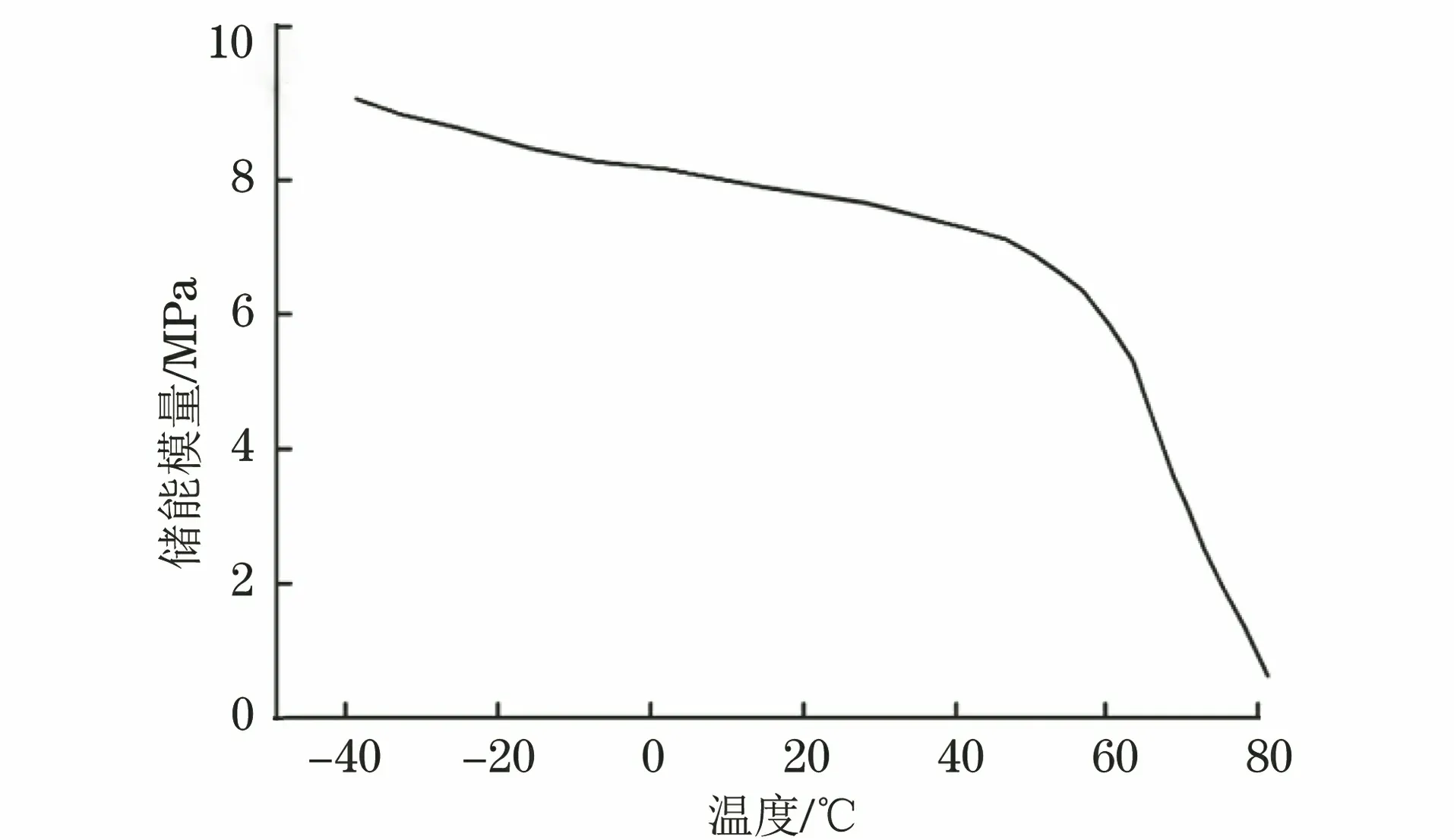
图5 环氧树脂灌封材料的储能模量随温度的变化曲线Fig.5 Curve of storage modulus vs temperature of epoxy resin potting material

由图5可以看出，该环氧树脂灌封材料的储能模量变化经历了3个阶段：第一阶段在-40～40 ℃，储能模量基本呈线性下降；第二阶段在40～70 ℃，储能模量呈非线性下降，特别地，在60 ℃时，储能模量开始急剧下降；第三阶段超过80 ℃后，储能模量趋于0。因此，该环氧树脂灌封材料的玻璃化转变温度约为55 ℃。

由表1可以看出，在玻璃化转变温度附近时，环氧树脂灌封材料的弹性模量急剧降低。

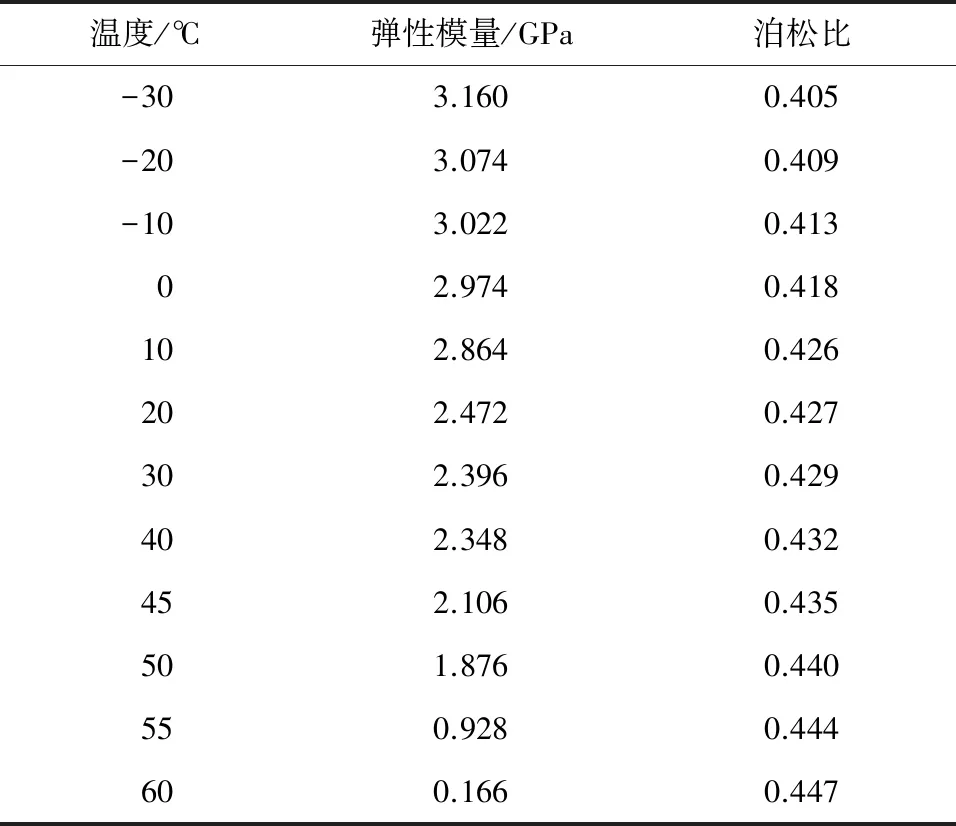
表1不同环境温度下环氧树脂灌封材料的弹性模量和泊松比Table 1 Elasticity modulus and Poisson′s ratio of epoxy resin potting material at different environmental temperatures

由表2可以看出：在玻璃化转变前，环氧树脂灌封材料的热膨胀系数随环境温度变化基本呈线性增加趋势；在玻璃化转变区内，热膨胀系数随环境温度变化呈非线性变化；在玻璃化转变后，热膨胀系数随环境温度变化又呈线性变化。

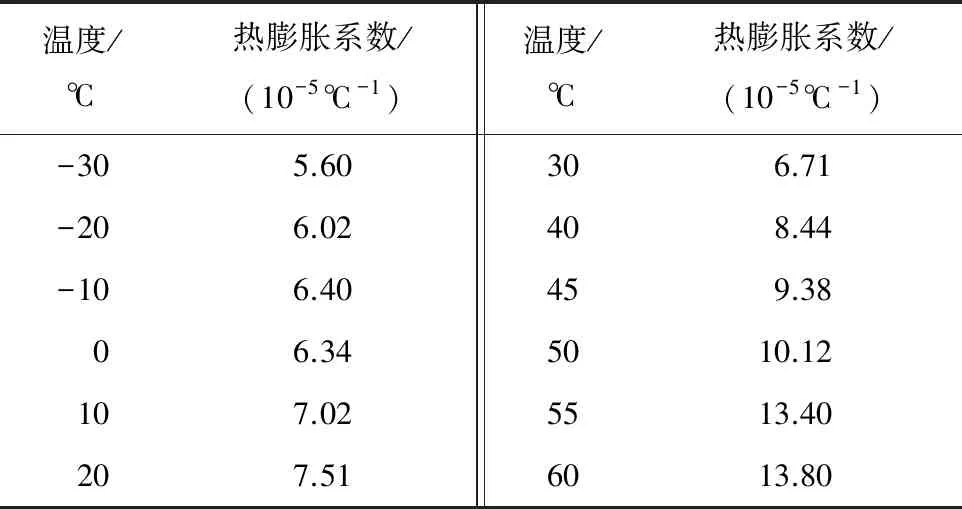
表2 不同环境温度下环氧树脂灌封材料的热膨胀系数Table 2 Thermal expansion coefficient of epoxy resin potting material under different environmental temperature

3.2 环氧树脂灌封材料的固化残余应变

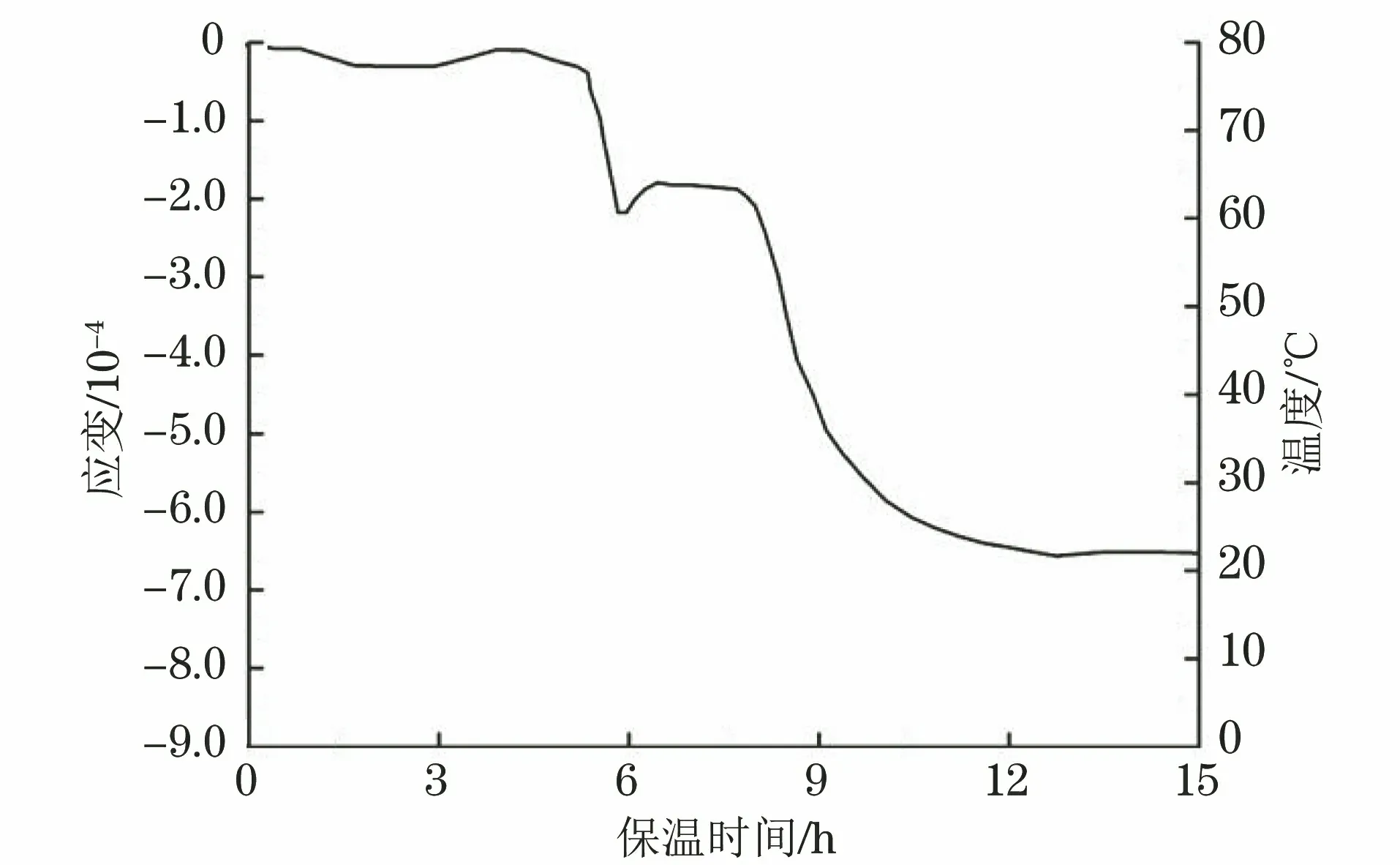
图6 环氧树脂灌封材料的固化残余应变测试曲线Fig.6 Curing residual strain test curve of epoxy resin potting material

由图6可以看出，当温度高于60 ℃时，随着保温时间的延长，环氧树脂灌封材料产生了较小的固化收缩应变；当温度为60 ℃时，环氧树脂灌封材料进入固化阶段，开始产生较大的固化收缩应变；当温度逐渐降至室温时，环氧树脂灌封材料产生明显的固化收缩应变；当温度达到20 ℃时，环氧树脂灌封材料完全固化，此时产生的应变为固化残余应变，约为-6.0×10-4，为收缩应变。根据表1中20 ℃时环氧树脂灌封材料的弹性模量为2.472 GPa，得到完全固化后的残余应力约为-1.5 MPa，为压应力。

3.3 灌封结构的热应变

与图4对应，由图7可以看出：高温段时，试样外表面中部的热应变约为1.8×10-3，上部的热应变约为中部的4倍，在8.0×10-3左右，下部热应变约为中部的3倍，在6.0×10-3左右，此时灌封结构产生拉伸应力；低温段时，中部的热应变约为-1.8×10-3，上部的热应变约为中部的3倍，在-5.2×10-3左右，下部热应变约为中部的2倍，在-3.5×10-3左右，此时灌封结构产生压缩应力。由上所述，在-30～60 ℃环境温度条件下，结合表1中的弹性模量，可估算该环氧树脂灌封结构的热应力为-16.5～1.3 MPa，远小于环氧树脂的断裂强度(100 MPa)，说明该环氧树脂灌封结构在-30～60 ℃环境温度范围内不会因为热应力导致开裂。

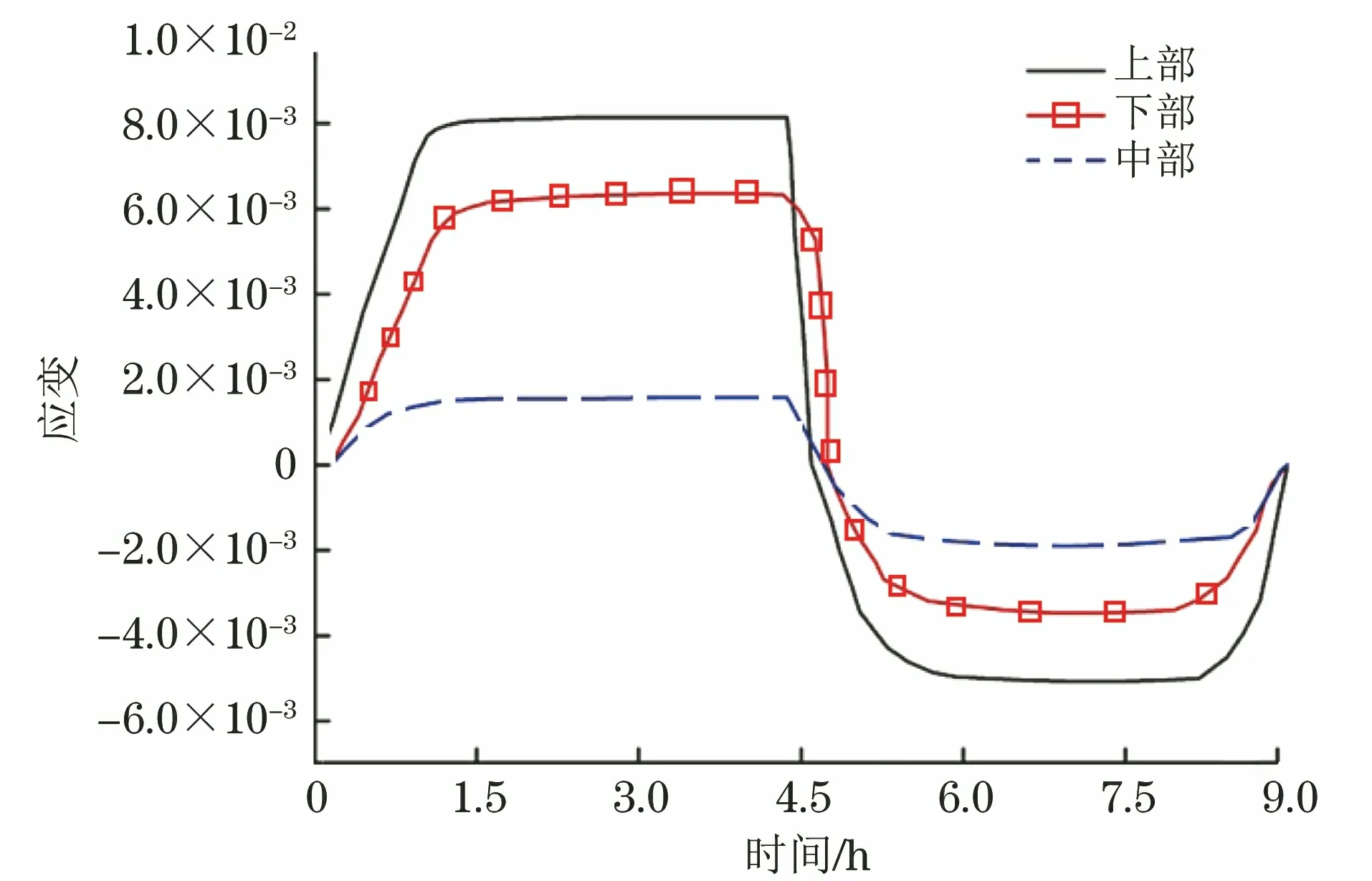
图7 环氧树脂灌封结构的热应变测试曲线Fig.7 Thermal strain test curve of epoxy resin casting structure

4 有限元模拟及验证

4.1 有限元模型

基于有限元分析软件建立了二维轴对称的环氧树脂灌封结构的有限元模型，如图8所示，采用自由和映射混合的方式划分网格，网格均为四边形单元，由于金属筒壁厚只有1 mm，重点对金属筒网格进行加密。为得到更真实的环氧树脂灌封结构的热应变分布，将环氧树脂灌封材料的固化残余应变测试结果作为初始边界条件加入环氧树脂灌封结构的热力耦合仿真模型中，并采用表1和表2随环境温度变化的环氧树脂灌封材料的力学和物性参数。在此基础上，计算所采取的边界条件如下：面A的y向位移为0；整体温度变化规律为从20 ℃升温至60 ℃，保温3 h后从60 ℃降温至-30 ℃，保温3 h，再从-30 ℃升温至20 ℃，温变速率均为1 ℃·min-1。

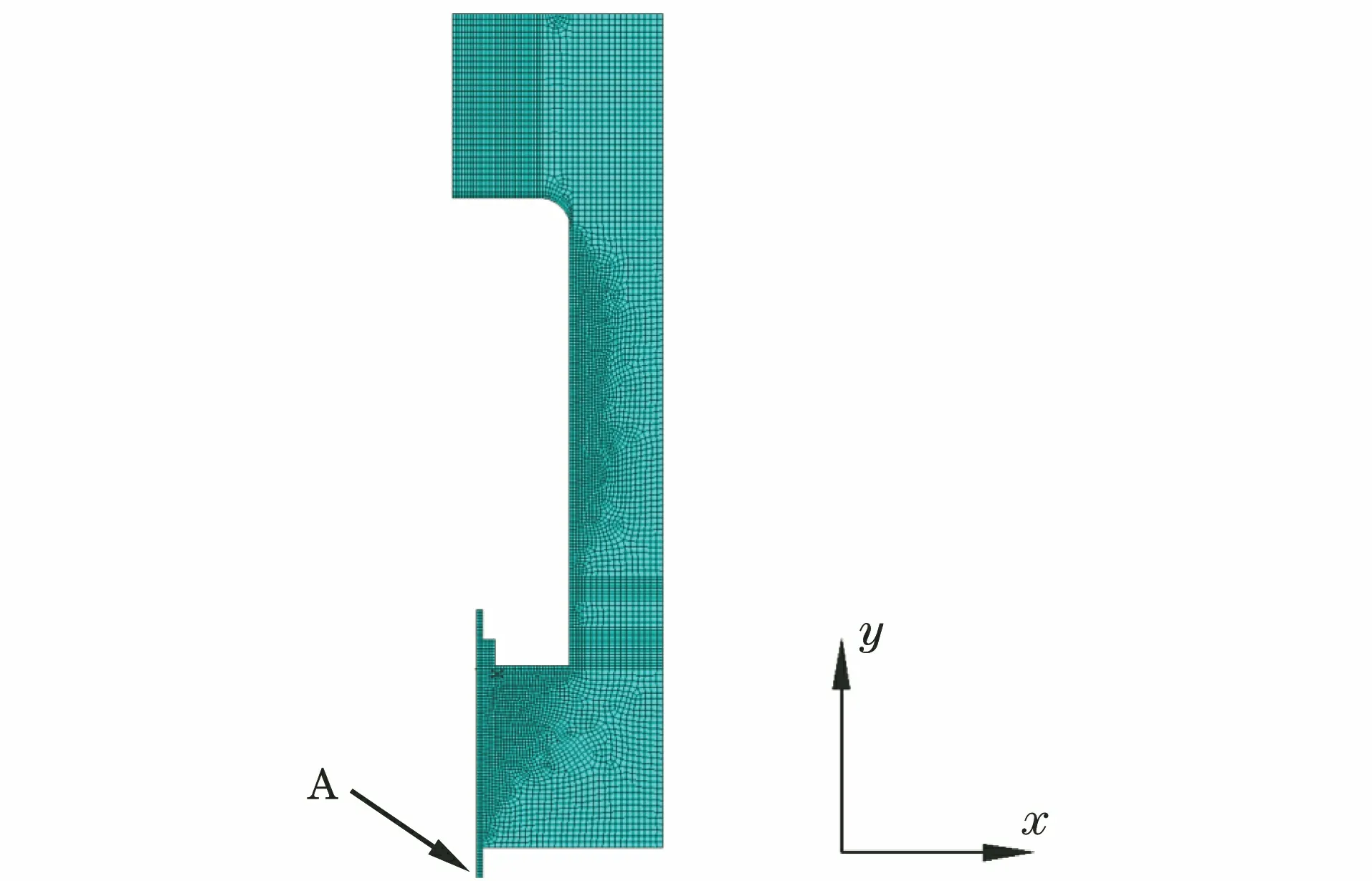
图8 环氧树脂灌封结构的有限元模型Fig.8 Finite element model of epoxy resin potting structure

4.2 模拟结果

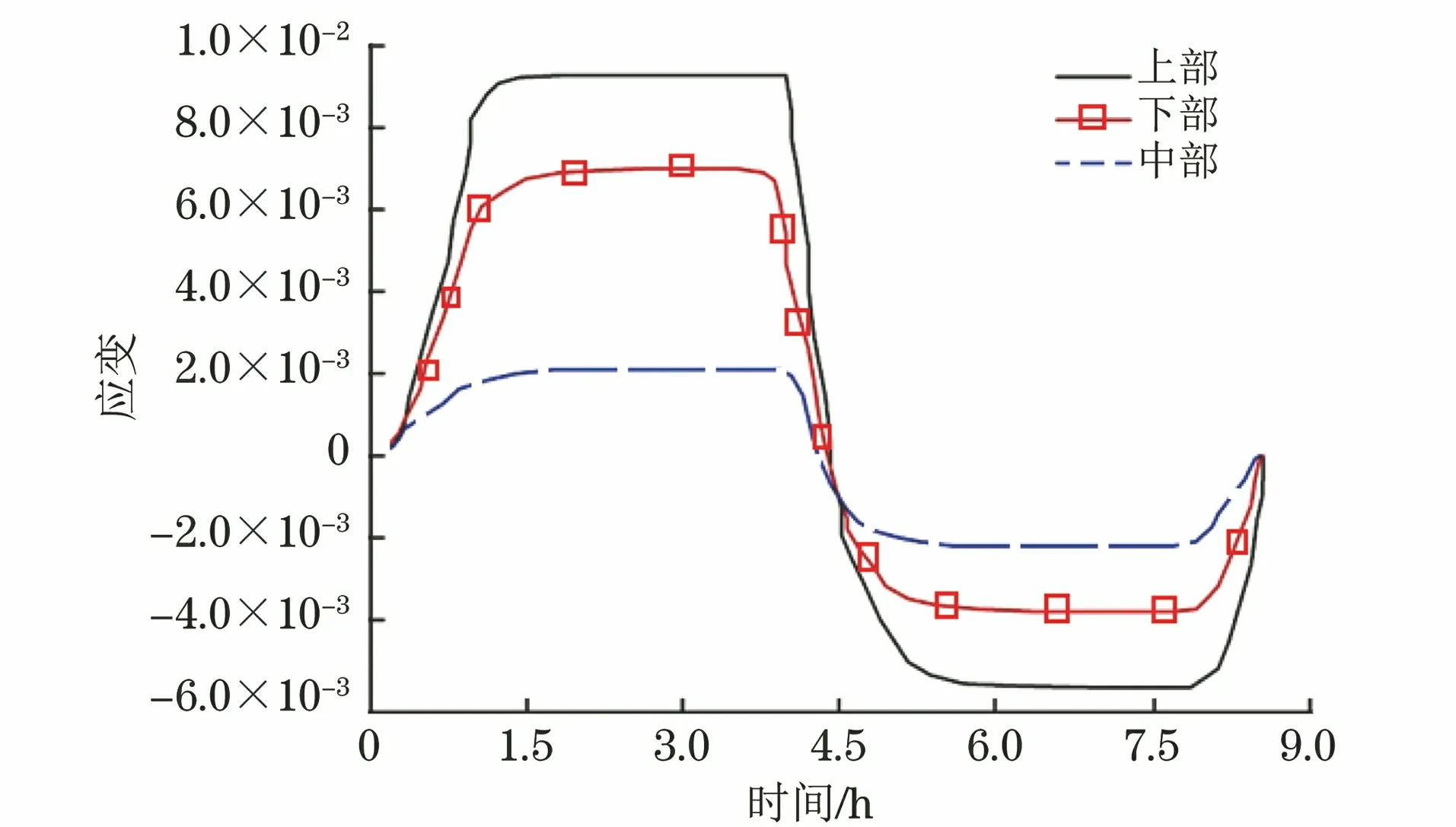
图9 环氧树脂灌封结构的热应变仿真曲线Fig.9 Thermal strain simulation curve of epoxy resin casting structure

由图9可以看出，高温段时，灌封结构外表面中部的热应变约为2×10-3，上部热应变约为中部的4倍，在9×10-3左右，下部热应变约为中部的3倍，在7×10-3左右，此时灌封结构产生拉伸应力；低温段时，中部的热应变约为-2×10-3，上部热应变约为中部的3倍，在-5.8×10-3左右，下部热应变约为中部的2倍，在-3.7×10-3左右，此时灌封结构产生压缩应力。由上所述，在-30～60 ℃仿真条件下，结合表1的弹性模量，可估算该环氧树脂灌封结构的热应力为-18.3～1.5 MPa。

环氧树脂灌封结构的仿真热应变与试验热应变存在相对偏差，在高温环境下，两者的相对偏差约13%，在低温环境下，两者的相对偏差约10%,高温和低温环境下的相对偏差均在工程允许范围内。

5 结 论

(1) 该环氧树脂灌封结构高温环境下的仿真热应变和试验热应变的相对偏差约13%，低温下约10%，相对误差均在工程允许范围内，有限元模拟结果较准确。

(2) 该环氧树脂灌封结构在-30～60 ℃范围内的热应力远小于其断裂强度，在该温度范围内不会因热应力而开裂。