数列的求通项与求和

广东省佛山市第一中学(528000)吴欣婷 吴统胜

广东省江门市开平市开侨中学(529300)杨雅文

本文举例说明了递推数列中求通项、求和的几种常用基本方法,对数列求和中涉及的常见放缩方法进行进行了较详细的探究、归类和总结,并得到了一些易于操作的一般性的放缩策略和方法.

一.常见递推关系求通项思路归纳

形式1累加(乘)法形如an−an−1=f(n)或其中f(n)可累加,g(n)可累乘;

形式2待定系数法形如an=pan−1+q(n∈N∗,n≥2)(p,q为常数,且p̸=1)的递推式,可用待定系数法转化为an+λ=p(an−1+λ),即转化为公比为p的等比数列求通项;也可用不动点法求通项(若方程x=px+q的根为α,则数列{an−α}是公比为p的等比数列);

形式5 形如an+1=pan+qan−1(n∈N∗,n≥2)的递推式,(教材《必修5》P69第6题)

方法1可用待定系数法转化为an+Aan−1=B(an−1+Aan−2)(n∈N∗,n≥3),即数列{an+Aan−1}是等比数列(注意该项是新数列第n−1项),再用形式4中的方法求解;

方法2(不动点法)如果x1,x2是递推关系an=pan−1+qan−2(n∈N∗,n≥3)的特征方程x2=px+q的两个实数解,则有:

(1)当x1̸=x2时,

(2)当x1=x2时,

这里α1、α2、β1、β2都是由初值a1,a2决定的常数.

形式6 形如的递推式,可两边先取对数,得转化为等比数列{ lgan}求an.

形式7 形如适当变形得kan=(kan−1)2,两边取对数,得lg(kan)=2lg(kan−1),从而可转化为等比数列{ lg(kan)}求an.

二、求和方法

1.公式法直接利用等差、等比数列求和公式求和或利用常见求和公式求和:

2.裂项法

3.错位相减法若数列{an}为等差数列,{bn}为等比数列,则数列{anbn}前n项和可用错位相减法求得.

4.分组求和法将通项拆成两项或多项,转化为公式法、裂项法、错位相减法等重新分组求和.

5.倒序相加法若数列中与首末两项等距的两项和总相等,可用倒序相加法求和.如等差数列求和公式的推导用的就是倒序相加法.

6.并项求和法若通项an有正有负,可采用并项求和法.凡是具有周期性质或类似于周期性质的数列求和均可采用并项求和法.

三.例题讲解

例1 求满足条件的数列{an}的通项公式:

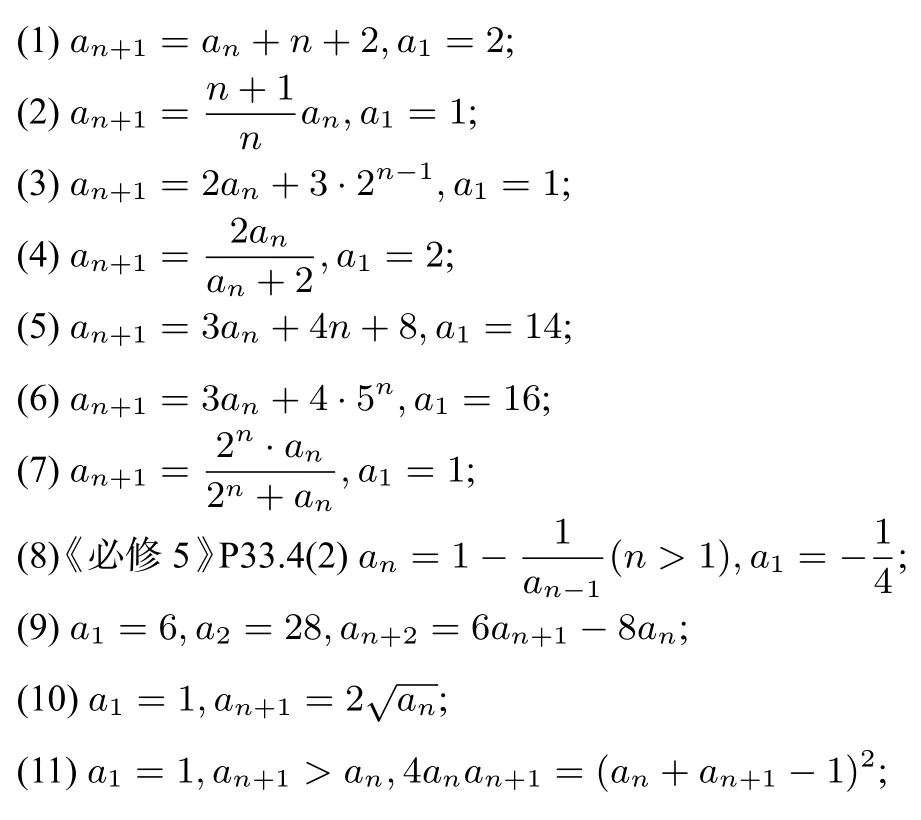
①+3×②得:

an+1+3bn+1=9(an+3bn),an=4·9n−3·2n,bn=8·9n+2n;或由①②消去bn,bn+1整理得:an+2=11an+1−18an,由形式5即可求得;

例2 (2010年全国理科第17题)设数列{an}满足a1=2,an+1−an=3·22n−1.

(1)求数列{an}的通项公式;

(2)令bn=nan,求数列的前n项和Sn.

解析(1)解法一(累加法)由已知,当n≥2时,an+1=[(an+1−an)+(an−an−1)+···+(a2−a1)]+a1=3(22n−1+22n−3+···+2)+2=22(n+1)−1.又a1=2,所以数列{an}的通项公式为an=22n−1.

解法二利用形式4(ii)直接转化为等比数列求通项

(2)(错位相减法)由bn=nan=n·22n−1知,Sn=1·2+2·23+3·25+···+n·22n−1①,从而22·Sn=1·23+2·25+3·27+···+n·22n+1②.①-②得(1−22)·Sn=2+23+25+···+22n−1−n·22n+1,所以

点评规律总结,解题关键在于和式两边同时乘以等比数列公比,两式错位相减即可转化为等比数列求和.一般地,若数列{an}为等差数列,{bn}为等比数列,则数列{anbn}前n项和Sn表达式必为Sn=(An+B)·qn−B,其中q为等比数列{bn}公比,故可由a1,a2的值求出待定系数A、B即可快速准确求出的表达式,此结论可大大提高错位相减法计算结果的准确性.

例3 (2010年全国理科第17题改编)已知数列{an}的前n和Sn=(n2+n)3n.

(I)求{an}的通项公式;(II)证明:

点评对通项进行了适当放缩转化为等比数列求和化简得证不等式.

例4 (2014年全国II理科第17题)已知数列{an}满足a1=1,an+1=3an+1.

解析(1)略;.

例5 (2012年广东理科第21题)设数列{an}的前n和为Sn,满足2Sn=an+1−2n+1+1(n∈N∗),且a1,a2+5,a3成等差数列.

(1)求a1的值;

(2)求数列{an}的通项公式;

点评放缩的目的是为化简求和,以上两例题证法一都是先放缩为等比数列,再求和化简.证法二是分离出非负数项进行放缩,放缩为等比数列求和化简,此放缩方法可操作性强,可实现精准放缩,是通性通法!

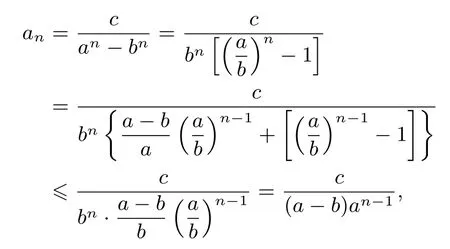
可快速转化为等比数列化简求和.2013年江西第17题也是此类题型.

常见放缩技巧主要有如下几种:

5.若0＜q＜1,则有

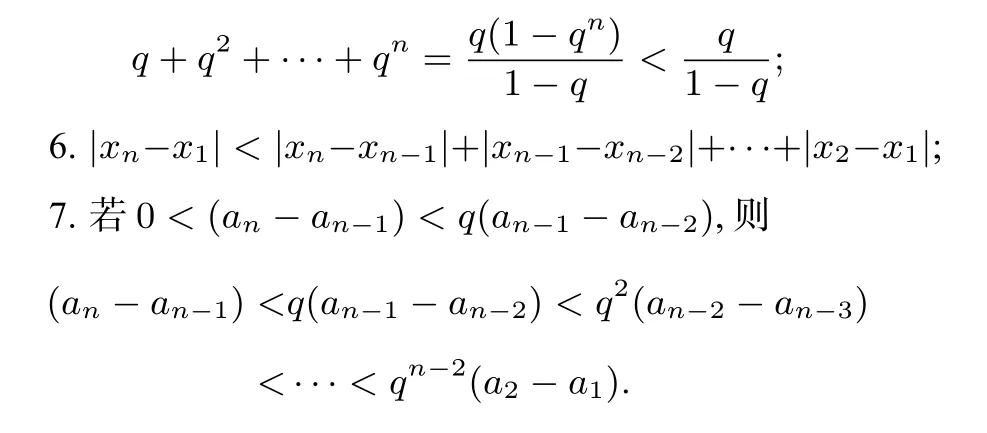
例6 (2014广东文科第19题)设各项为正数的数列{an}的前n和为Sn,且Sn满足

(1)求a1的值;

(2)求数列{an}的通项公式;

(3)证明:对一切正整数n,有

点评本例是裂项相消法,将通项裂成结构特征相同的前后两项的差的形式,前后项中的部分式子相互抵消,从而可化简求和得证.

点评本例是先裂项求和再放缩证明不等式.由于放缩法灵活多变,技巧性要求高,所谓“放大一点则太大,缩小一点则太小”,让学生解题时很茫然.突破的关键是让学生弄清放缩法的思路和目标是怎么来的,熟练掌握各种数列放缩的方法和技巧.

点评本例题采用的是分离出非负数项进行放缩,放缩为等比数列求和化简,此放缩方法可操作性强,可实现精准放缩,是通性通法,应引导学生理解和掌握该放缩方法!

四.反馈练习

1.(2009全国II第19题改编)设数列{an}的前n项和为Sn,已知a1=1,Sn+1=4an+2.

(I)设bn=an+1−2an,证明数列{bn}是等比数列;

(II)求数列{an}的通项公式;

(III)求数列{an}的前n项和Sn.

2.已知数列{an}的前n项和为Sn,且Sn=2an−2;数列{bn}满足b1=1,bn+1=bn+2,n∈N∗.

(I)求数列{an},{bn}的通项公式;

(II)记cn=anbn,n∈N∗.求数列{cn}的前n项和Tn.

3.(2008江西文科第19题)等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.

(1)求an与bn;

4.已知数列{an}的各项均为正数,其前n项和为Sn,且满足

(1)求a2的值;

(2)求数列{an}的通项公式;

(3)是否存在正整数k,使ak,S2k−1,a4k成等比数列?若存在,求k的值;若不存在,请说明理由.

5.(2009湖北文科第19题)已知{an}是一个公差大于0的等差数列,且满足a3·a6=55,a2+a7=16.

(I)求数列{an}的通项公式;

(II)若数列{an}和数列{bn}满足等式:(n为正整数),求{bn}的前n项和Sn.

6.(2015全国)Sn为数列{an}的前n项和.已知an＞0,

(I)求{an}的通项公式;