对近年来全国一卷理科数学解析几何的命题分析

广东省广州科学城中学(510530)李健康

解析几何作为高考数学试题的几何压轴题,历年来对于高三的学生而言都具有一定的恐惧感,该题目一般分成两问,第一问属于较为基础的基础知识或概念的运用,求解,一般求圆锥曲线的解析式或轨迹或其它,难道中等;主要就是第二问较为复杂,设及到各种知识的综合运用,使学生无从入手,或难于入手,或虽初步尝试解答,其后由于参数多变,无法应对,终是无功而返!

有感于此,本人对2014-2017年度全国一卷、二卷、三卷的所有圆锥曲线题目进行了解答和分析,发现了一些命题规律,由于篇幅的关系,下面就全国一卷的理科解析几何题目做一个较为详细的探讨:要想解决该题目,必须做好一定的知识准备,主要涉及到的知识有:

1、一般的圆锥曲线求解知识,如a、b、c之间的关系,e、渐近线、斜率和各种圆锥曲线的概念知识;

2、韦达定理的恰当运用,特别是弦长公式、中点公式、斜率公式等在变化中使用;

3、方程思想、函数最值思想、垂直关系中斜率关系和向量关系的使用;

4、一些求距离的公式:如点到直线的距离公式、弦长公式、勾股定理等.

下面我就2014-2017年度题目来对以上知识进行分析:

一、2014年全国理数一卷题目

(I)求E的方程;

(II)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程.

分析该题的第一问(图一)比较简单,A(0,−2)是已知固定点,F(C,0)是焦点,AF斜率为直接用两点斜率公式建立方程得又所以a=2,b2=a2−c2=1,故E的方程为

图1

图2

第二问详解如下:

总结1、对于直线要讨论斜率k的两种情况,2、用弦长公式前要注意直线与圆锥曲线的联立方程后∆的先决条件,3、确定函数关系后,求最值时要灵活使用换元法、基本不等式等来求解.

命题意图考察分类思想、知识掌握的完整性、求最值思想方法、思维的灵活性.

二、2015年全国理数一卷题目

在直角坐标系xOy中,曲线C:与直线l:y=kx+a(a＞0)交于M,N两点.

(I)当k=0时,分别求C在点M和N处的切线方程;

(II)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.

分析对于第一问而言,还是比较简单的,画出草图(图三)后不难看出:把y=a代入即可求出利用导数求出过M、N点的切线斜率,再利用点斜就可求式出相应的切线方程.

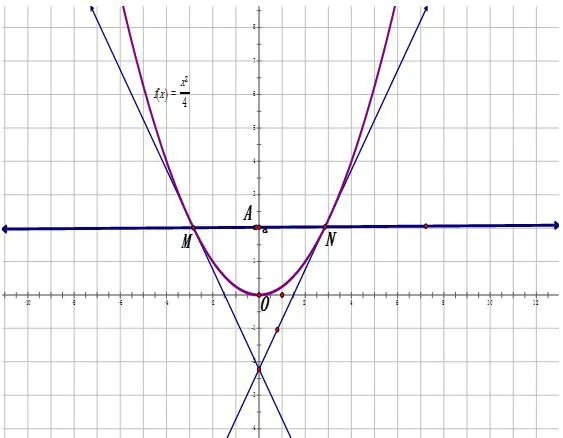
图3

对于第二问,我们同样画出草图(图四)进行分析:假设存在P(0,b),M(x1,y1),N(x2,y2),于是在k变动时,怎样才总有∠OPM=∠OPN呢?事实上,由图像我们可以知道如果∠OPM=∠OPN,则必有kMP和kNP互为相反数,即kMP+kNP=0;由于直线l过固定点A(0,a),事实上,直线l只含有一个参数k,把l:y=kx+a代入后所得到方程x2−4kx−4a=0,此时x1+x2=4k,x1x2=−4a;利用y=kx+a和kMP+kNP=0即可建立一个含有参数k和b的等式(a是个常数).问题就转化为:是否存在b,使得无论k如何变化,等式恒成立.

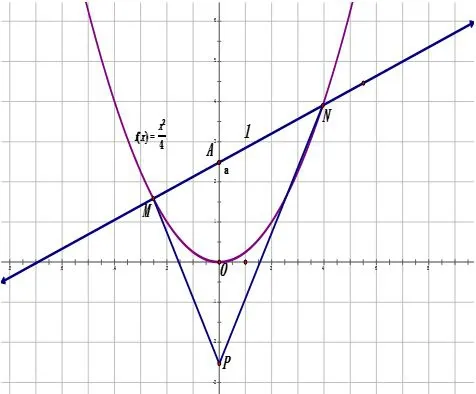
图4

第二问详解如下:

设P(0,b)为符合题意的点,M(x1,y1),N(x2,y2),直线PM,PN的斜率分别为kMP,kNP,把y=kx+a代入C的方程,得x2−4kx−4a=0.故x1+x2=4k,x1x2=−4a.从而

总结直线含有一个参数(a看做常数),与圆锥曲线得到二次方程,利用韦达定理,再利用kMP+kNP=0来建立等式,从而求解.此题的关键在于由∠OPM=∠OPM推出kMP+kNP=0,熟练使用斜率公式和韦达定理进行综合建立方程.

命题思路第一问简单的切线求解,目的在于为第二问提出问题.第二问的求解就在于考察学生对斜率的综合使用,包括斜率公式与韦达定理的糅合,包括斜率与图形位置关系的糅合,考察学生对于含多参数数学式子的处理.

三、2016年全国理数一卷题目

设圆x2+y2+2x−15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.

(I)证明|EA|+|EB|为定值,并写出点E的轨迹方程;

(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.

分析对于第一问,把圆x2+y2+2x−15=0化成标准方程(x+1)2+y2=16,画出草图(图五)由图中我们可以看出:因为EB//AC,所以∠1=∠C,而∠C=∠D,故∠1=∠D,所以EB=ED,所以EA+EB=AD=4,由于点A(−1,0)和点B(1,0)均为固定点,E为动点,即点E满足椭圆的定义,有c=1,2a=4,从而求出椭圆.

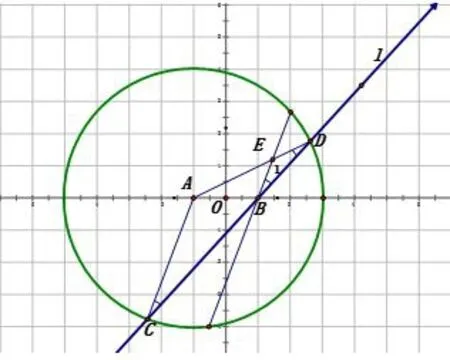
图5

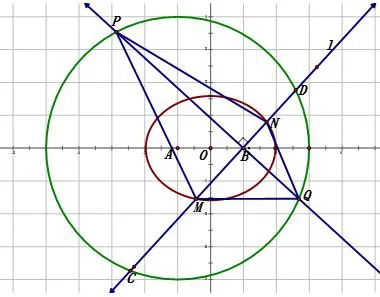
图6

两问详解如下:

解(I)因为|AD|=|AC|,EB//AC,所以,∠1=∠C,∠C=∠D,故∠1=∠D.所以|EB|=|ED|,故|EA|+|EB|=|EA|+|ED|=|AD|.又圆A的标准方程为(x+1)2+y2=16,从而|AD|=4,所以|EA|+|EB|=4.由题设得A(−1,0),B(1,0),所以c=1,2a=4,得由椭圆定义可得点E的轨迹方程为:又由于直线l过点B(1,0)且与x轴不重合,所以y̸=0.

总结该题的第一问有一定的技巧性,主要是和为定值问题,我们就可以联想椭圆的定义,再根据题目的一些条件,就可以确定.这一问最容易失分的是y̸=0这里,容易漏掉直线l与x轴不重合这条件.第二问,考察的知识点同样是我们熟悉的含有一个参数的直线方程,弦长的两种求法,直接弦长公式法,点到直线的距离公式、垂径定理的使用、勾股定理在圆内求弦长法;函数问题求最值.

命题思路考察的模式与2014年基本一样,第一问求椭圆的标准方程,难度略有提高;第二问,涉及到直线与圆锥曲线的组合,直线还是过定点含有一个参数k的直线,使用到弦长公式,点到直线的距离公式,但增加了圆内求弦长的做法,最后还是构造了函数求最大、最小值来求值域的问题;这次没有使用基本不等式,使用了反比例函数思想.2014和2016都涉及到了分类思想.

四、2017年全国理数一卷题目

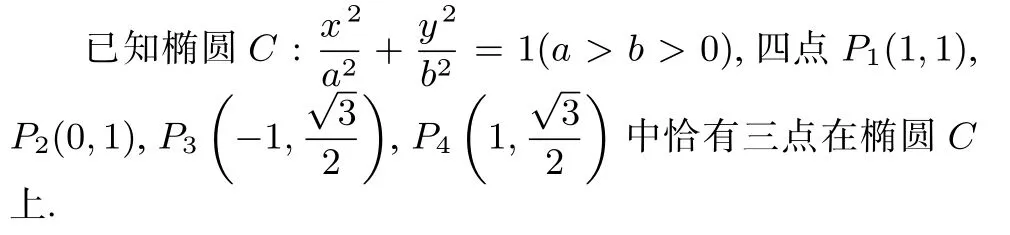
(1)求C的方程;

(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.

第二问:难度较大,故可以画出草图进行分析设直线直线P2A与直线P2B的斜率分别为k1,k2;由于直线l的任意性,故斜率k需要讨论.

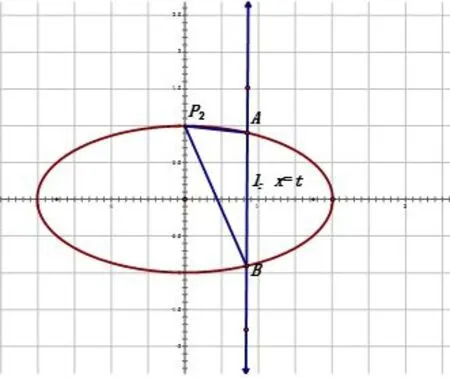
图7

2、当k存在时(图八),可设l:y=kx+m,代入椭圆方程得x1+x2和x1x2都含有参数k和m,再利用P2(0,1)、k1+k2=−1,可以找到k和m之间的关系,再次代入直线l,于是题目就变成了一条直线中含有一个参数时过定点的问题,从而得解.

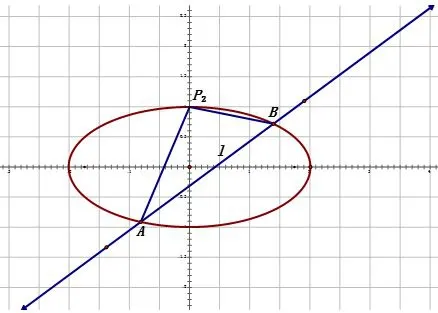
图8

第二问详解如下:

(2)设直线P2A与直线P2B的斜率分别为k1,k2.

1、当k不存在,即l⊥x轴时,设l:x=t,由题设知)t̸=0,且|t|＜2,可得A,B的坐标分别为则

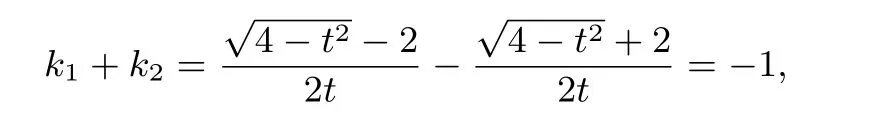
得t=2,不符合题设.

2、当k存在时,可设l:y=kx+m,将y=kx+m代入得

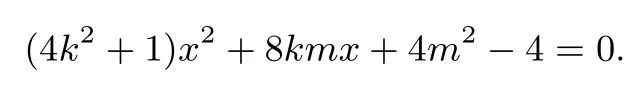
总结第一问是属于椭圆的基本知识考察,比较基础;第二问同样是直线问题,但该直线含有两参数,要讨论k的情况,利用直线与圆锥曲线联立方程组,使用韦达定理计算x1+x2和x1x2,再利用斜率公式和给出的条件k1+k2=−1,找出两个参数之间的关系,代入原来直线,从而进行转换从含一个参数的直线方程过定点的问题.

命题思路第一问考察圆锥曲线基本知识运用求椭圆,基础性考察;第二问考察的是含有参数的动直线与圆锥曲线组合的问题,利用给出的一个等式,把两个参数的问题化成一个参数的问题再转化为含有一个参数直线方程过定点的问题.

纵观从2014-2017年全国一卷理科数学解析几何题目可以看出一定的命题规律,并提出有关的2018年高考理科解析几何复习思路,如下:

1、奇偶年题目命题思路相似性,即偶数年的思路相似,奇数年的思路相似.2014年和2016考察的题目,第一问都是通过圆锥曲线的基本知识或概念,求椭圆方程;第二问,都涉及到了面积问题,题目都使用的思想方法有:联立方程组使用韦达定理,使用弦长公式,使用点到直线的距离公式,函数求最值思想,都涉及使用过一个固定点的直线,使用斜率k做参数,涉及到斜率k的分类讨论.

2、2015年和2017年考察的题目,第一问主要还是圆锥曲线的基础知识求解;第二问,都涉及到的问题有:表面的直线均含有两个参数(事实上2015年只有一个,参数a是看做常数,2017年的确实含有两个参数),联立方程组使用韦达定理,题目都直接给出或隐含给出所涉及的两条直线斜率k之间的等量关系,都利用两点求斜率k的公式,结合韦达定理,找出两个变量之间的关系.从以上我们可以看出,2014和2016年、2015年和2017年的命题思路基本一致,可以大胆预测,2018年全国一卷理科数学的命题思路很有可能与2014、2016年相似.

3、再结合2014-2017年全国二卷和三卷的题目分析,同样也发生了类似的情况,即命题带有一定的连续性和规律性,故在此可以提出2018年面对全国一卷的理科数学解析几何题的复习建议:(1)注重圆锥曲线的概念、基本知识、基本求解方法的教学,特别是椭圆;(2)设好过固定点直线,注意讨论k的存在情况,使用好韦达定理,使用好弦长公式;(3)在函数章节的教学中,注意函数最值问题的求解,特别是基本不等式求最值、二次函数求最值等,在圆锥曲线练习题目中要有所体现;(4)当然,不能把宝都押在偶数年思路上,时间允许,也应该把奇数年的思路尽可能的教给学生.