中考数学试题中的应用性问题与解题技巧的研究

安徽省合肥师范学院数学与统计学院(230601)阮征

一、引言

中考数学试题是命题人员集体智慧的结晶,也是广大数学教师进行教学研究的重要素材.如何深入领悟中考数学试题的突出特色和教学价值也一直是我们关注的重点.而中考数学试题应以数学课程标准为依据,以学生发展为本,全面考查学生对“双基”的掌握、数学思考水平、解决问题的能力;试题素材的背景要密切联系学生的实际生活,贴近学生的认知水平;更要注重学生动手操作能力和创新探究能力.近年来,各地中考命题出现了信息类、环保类、建模类、学科综合类等众多新型应用题,在近几年安徽省中考数学试题中,我们可以发现中考数学命题改革的趋势中应用性问题已成为中考数学的必考题和经典题型,出应用性题目的宗旨是引导学生从已有的知识和生活经验出发,在解题过程中体会数学与生活的密切联系以及感受生活中的数学美.

波利亚强调指出:“中学数学教学首要的任务就是加强解题训练.”有很多初中生总是为学习数学烦恼,参加中考时,他们的数学总是很难考到自己理想的分数,这其中很大的原因就在于他们的数学基础薄弱、解题技巧欠缺,只记得那些死板僵化的方法,而不会灵活运用,对应用性题目表现出束手无策.所以研究中考数学中的应用性问题及其解题技巧具有非常重大的意义.

二、剖析中考数学应用性问题

剖析安徽省近几年的中考数学真题,可以将考查的应用性问题简要概括为方程与方程组、不等式与不等式组、函数、概率与统计、几何五大类,而初中数学的各个领域恰好涵盖在这五大类应用性问题中,并且与我们的日常生活息息相关,所以关注热点问题、把握中考动向,让学生把握好应用性问题的解题方法和技巧,使学生在这类题目上不失分、少失分是每个数学教师的当务之急.

(一)中考数学应用性问题常考的热点聚焦

1.基本关系(复利问题)

基数×(1+平均增长率)n=n次增长后的到达数;

基数×(1−平均增长率)n=n次增长后的到达数;

2.其他公式

本金×利率×所定期数=利息(单利问题);

本金+利息=本息;

毛收入=卖出价−购进价;

增长率=增加数量/原本数量×100%;

降低率=减少数量/原本数量×100%.

(二)中考应用性问题的常考模型

1.方程模型

2.不等式模型

3.函数模型

4.统计模型

5.几何模型

(三)中考数学应用性问题的解题思路

中考数学中的应用性问题的解题思路可以概括为阅读、理解材料给出的信息、将实际问题转化为数学问题、利用所学知识解决问题、最后再运用到实际问题等步骤,这是解决应用性问题最常用的建模思想,当然,不同的应用性问题运用到的解题方法和思路也是不同的.

三、试题再现

(2006年安徽省第18题)汪老师要装修自己带阁楼的新居(下图1为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角F碰头,设计墙角F到楼梯的竖直距离FG为1.75m.他量得客厅高AB=2.8m,楼梯洞口宽AF=2m,阁楼阳台宽EF=3m.请你帮助汪老师解决下列问题:

图1

(1)要使墙角F到楼梯的竖直距离FG为1.75m,楼梯底端C到墙角D的距离CD是多少米?

(2)在(1)的条件下,为保证上楼时的舒适感,楼梯的每个台阶小于20cm,每个台阶宽要大于20cm,问汪老师应该将楼梯建儿个台阶?为什么?

解(1)根据题意有AF//BC,所以∠ACB=∠GAF,又∠ABC=∠AFG=90°,所以△ABC∼△GFA所以得BC=3.2(m),CD=(2+3)−3.2=1.8(m).

(2)设楼梯应建n个台阶,则解得14＜n＜16.所以楼梯应建15个台阶.

(2007年安徽省第23题)

按下图2所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据.要使任意一组都在20−100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:

(I)新数据都在60−100(含60和100)之间;

(II)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大.

图2

(1)若y与x的关系式是y=x+p(100−x),请说明:当时,这种变换满足上述两个要求;

(2)若按关系式y=(x−h)2+k(a＞0)将数据进行变换,请写出一个满足上述要求的这种关系式.(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)

(2)本题是开放性问题,答案不唯一.若所给出的关系式满足:(a)h≤20;(b)若x=20或100时,y的对应值m,n都能落在60−100之间,则这样的关系式都符合要求.

如取h=20,y=a(x−20)2+k,

因为a＞0,所以当20≤x≤100时,y随x的增大而增大.令x=20,y=60,得k=60①令x=100,y=100,得a×802+k=100②由①②解得,所以

(2009年安徽省第19题)学校植物园沿路护栏的纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm.如图3所示,已知每个菱形图案的边长为其中一个内角为60°.

图3

(1)若d=26cm,则该纹饰要用231个菱形图案,求纹饰的长度L;

(2)当d=20cm时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?

解(1)菱形图案水平方向的对角线长为根据题意,L=30+26×(231−1)=6010cm.

(2)当d=20cm时,设需要x个这样的菱形图案,则有:

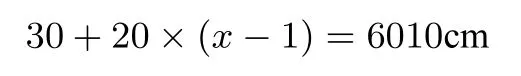
解得x=300,所以需要300个这样的菱形图案.

(2009年安徽省第23题)已知某种水果的批发单价与批发量的函数关系如图4所示.

(1)请说明图4中①、②两段函数图象的实际意义;

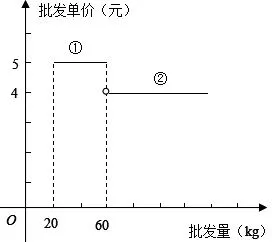
图4

(2)写出批发该种水果的资金金额w(元)与批发量n(kg)之间的函数关系式;在下图5的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果.

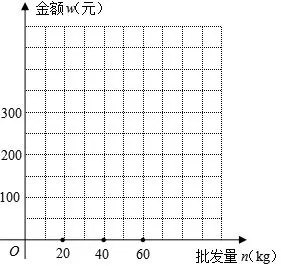
图5

(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图6所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.

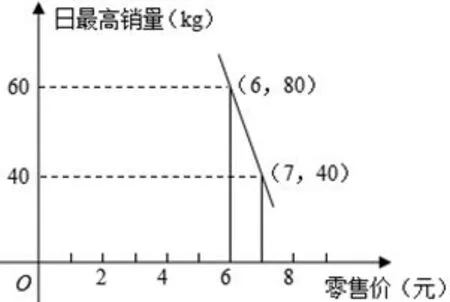
图6

解(1)①表示批发量不少于20kg且不多于60kg的该种水果,可按5元/kg批发;

②表示批发量高于60kg的该种水果,可按4元/kg批发.

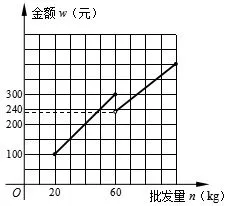
图7

由图可知,资金金额满足240＜w≤300时,以同样的资金可批发到较多数量的该种水果.

(3)设日最高销量为xkg(x＞60),日零售价为p,设x=pk+b,则由图(2)该函数过点(6,80),(7,40),代入可得:x=320−40p.于是销售利润从而x=80时,ymax=160.此时p=6,所以经销商应批发80kg该种水果,日零售价定为6元/kg,当日可得最大利润160元.

(2012年安徽省第23题)如图8,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x−6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.

(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围);

(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;

(3)若球一定能越过球网,又不出边界,求h的取值范围.

图8

(3)根据题设知y=a(x−6)2+h.由图象经过点(0,2),得36a+h=2①.由球能越过球网,得9a+h＞243②.由球不出边界,得144a+h≤0③.由①②③解得所以h的取值范围是

四、解题技巧探究

上面列举的5道应用性问题分别涉及的是台阶问题、数据输入问题、护栏问题、销售问题、投球问题,那么通过分析这些应用性问题的解题思路,我们可以发现,解决这类应用性问题首先要调查题意,迅速找到概念所在,并以此为“面”;透过题目的叙述,抓住重点词句,提出重点数据,并以此为“点”;综合联系,提炼当中的关系,根据数学方法,建立数学模型,并以此为“线”,这样就将应用性问题转化为纯数学问题,然后利用所学知识解决问题、最后再运用到实际问题,即按照实际问题→分析、联想、转化、抽象→建立数学模型→解决数学问题→解决实际问题的思想方法解决应用性问题.

五、结论

现如今,应用性问题被越来越多的命题者采用,各地中考都加强了应用性问题的考查力度,命题的设计也出现了格局新颖、结合实际的新趋势,从前面的分析中我们不难发现:中考数学应用性的发展方向正朝着强化应用性问题的考查和创新中考试题的形式变化,这种趋势的用意是培养学生的应用意识和数学建模思想.而应用性问题都是与学生的日常生活息息相关的问题,而且应用性问题特点鲜明、内容丰富、形式多样,但涉及的数学知识并不深奥,也不复杂,只是题目的文字材料较长,重点考查学生的阅读理解能力、文字概括能力、数据处理能力、推理分析能力、书面表述能力以及随机应变能力,要求学生在反复阅读、透彻理解的基础上,综合题目所提供的数据与信息进行分析,这样既有利于帮助学生从数学的角度发现问题打开解题思路,又提高了学生的创造力和想象力,更让学生进一步体会到了数学的应用价值.所以在在应用性问题解题时一定要有耐心,仔细阅读,细心领会,找出题目想考查的内容和知识点,灵活运用相关只是和方法,将实际问题转化成数学问题来解决.所以数学教师在平时的数学教学中必须收集贴近生活实际的热点问题,再把它们设计成既贴近生活又贴近课本的应用性问题,这样既能激发学生的学习兴趣,又能培养学生分析解决应用性问题的技巧,从而使学生在中考中不失分、得高分.