多元表征：突破儿童思维品质发展的瓶颈

姚超 卓元

摘  要：儿童思维在发展过程中，总会遇到困顿的现象，就像一个“淤结”堵在前行的路上，于是阻止了儿童良好思维品质的发展。致使其思维外显、可视性不强，导致儿童在思考问题过程不能做到深刻与广阔，笔者通过引导学生“你能让别人一眼就看明白你的思路吗”“动手操作比言语表述效果要好”“谁有不一样的想法”等促使思维表征多元化的外显、可视，打通了儿童思维品质发展的“最后一英里”。

关键词：表征;多元化;思维品质;突破瓶颈

课堂教学中有时当一个问题出现的时候，经过学生深入思考或在教师引领下的思索，对问题的理解与掌握有了突破，就是所谓的“会做了”。当这些“会做了”的学生，去引领或分析讲解其解决过程与策略时，他讲得头头是道，而别人听来是一头雾水似懂非懂;有时学生知道怎么做，却说不出为什么这样做，就像平时所说的“1+1=2”，为什么等于2却没有学生接着说下去。难道学生在思维中真的不明白吗？不是，而是学生不知如何将问题的结论表征外显、可视化。笔者在教学中每每遇到这种情况，都会停顿下来结合实际，引导学生将内隐进行外显、可视达到共享。

一、你能让别人一眼就看明白你的思路吗？

思路决定着出路。好的思路就会有好的出路，也为同伴指出了前进的道路。数学的学习过程就是明白一个“理”的过程，这个“理”就是常说的“算理”，做到知其然还要知其所以然。这样学生才会真正掌握、理解问题，并内化成自己的东西。当下次用到该知识点去解决问题或生发问题时，无须刻意理解，便会自然生发，就像吃过饭长肉增高一样，吃进去的饭看不到，但长高变胖却是外显可视的。所以，要引领学生将内隐的东西进行外显、可视，达到合作共赢、互相补充，使明白的更加明白，使不足之处得到弥补。教学苏教版四年级下册《解决问题策略》中，该解决问题的策略是画线段图或示意图，是借助几何直观把复杂的数学问题变得简明形象，使学生在直观下理解数学。直观理解数学问题最直接的描述方式，就是用图把抽象的数学问题直观地表示出来，进而使问题与条件之间的联系形象、生动，借助直观图分析数量关系寻求解题思路。这是不断积累解决问题经验，感悟直观化思想方法，发展几何直观，提高分析、解决问题能力的过程。学生完整地经历了“理解题意—分析数量关系—列式解答—检验反思”的过程后，面对富有变化的问题进行挑战性的解决。与教材相配套的苏教版《练习与测试》76页“应用广角”中一题：一个边长8米正方形，把它一组对边增加3米，另一组对边增加5米，得到的长方形面积是多少平方米？问题出现，学生反映不够热烈，于是请唯一举手的刘家乐帮大家分析，该生站起来直接说8+3=11米，8+5=13米，13×11=143平方米，得到长方形面积是143平方米。而其他学生听完后从眼神中显出不明白的疑虑。一个问题的解决让所有的学生释怀才是最好的境界。有疑虑就不能轻松放过。“请你再给大家讲解一遍。”对他提出了要求。他只是对刚才的内容重复了一遍，学生们的眼神依然还是那种疑虑。“你能让别人一眼就看明白你的思路吗？”这是对他的询问。“既然解决问题，就要充分地运用解决问题的策略。”他在我的提示后，略沉了几秒，然后在黑板上画一个正方形：

“一组对边增加3米。”在一组对边画出了增加的3米。

“另一組对边增加5米。”然后在另一组对边画出增加的5米（如图1）。

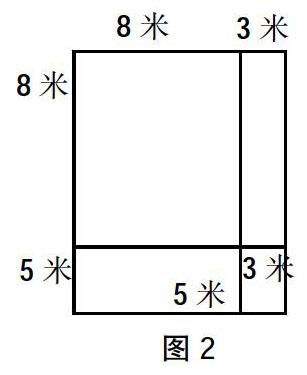
习题中说两组对边增加后得到一个长方形，而现在却是长方形缺了一角，应怎么办？这另外一组对边不应该说是原来正方形的对边，而是一组对边增加3米后图形的对边，形成正确图形是这样的，对他画的图形做了调整，如图2。

简单的一句提醒，由原来的解决问题的语言表征转换成直观的图形，通过这个图形所有学生都清楚明白了一组对边增加3米，另一组对边增加5米，所得到的长方形图形，求其面积就迎刃而解了。有时候就是这样，同样的内容换一种表征方式就会豁然开朗。看来一句“你能让别人一眼就看明白你的思路吗”，确是理解问题的另一条出路。刘家乐从自己的直观图形表征下，加深了对此问题的理解，同学们也知道长方形得来的原因。图形的直观表征方式，使学生感受到画图描述和分析问题，对问题解决的价值。这培养了学生的几何直观，提高分析和解决问题的能力，获得了解决问题的成功体验，树立学好数学的信心。

二、动手操作比语言表述效果要好

对数学内容表征的形式是多样的。有一位老师谈到引导学生对1/2的表征，有的是“二分之一”;有的用一个苹果仔细地从中间一开两半，其中一半是1/2;有的说班级有40名同学，其中男生20人，男生人数占班级人数的1/2……不管采用什么样的表征方式，最终目的在于创新，让对方清晰明了。有些数学内容，即使用语言描述得再细致，但在学生的思维当中仍然形成不了其理解下的思维表征，对于此类内容只可意会不可言传。在认识长方形、正方形基础上，继续深入学习三角形。三角形的三边关系不能仅局限于一个结论：三角形任意两边之和大于第三边。但其后还有一个对学生思维发展跳跃的台阶，那就是三角形稳定性的特征。彻底理解了三角形稳定性特征，学到的不仅仅是数学知识，而且丰富了生活体验，从这一点来说就把数学与生活结成一家亲。

师：同学们理解了三角形三边之间关系：三角形任意两边之和大于第三边。现在做一个实验，用3根木条钉成三角形框架用力去拉，看看三角形框架形状会发生变化吗？先猜测一下。

生：不会变。

生：会变。

师：根据这两种结论，我们用事实说话。（安排学生拉三角形框架进行实验）

生（齐说）：没有变化。

师：正因为三角形有这个特征，所以许多物体上都用三角形的结构。现在这个小方凳的腿活动了，怎么办？（拿出方凳子进行晃动）

生：斜钉一根木条成三角形就不晃动了。

师：（钉上木条后，用力晃动）为什么钉上木条就晃不动了呢？这里有一个长方形和一个三角形，用锤子顺着一个角用力敲，看看形状会不会变化？

生：长方形的形状会变，三角形的形状不变。

师：（教师用锤子分别去敲打）结果是三角形的形状不变，这一点充分证明了三角形的稳定性：当一个三角形的三条边长度确定后，这个三角形的形状、大小就不会改变。

教师无论用什么样的语言描述三角形稳定性的特征，都不如用直观形象的动手操作表征来“表述”，学生易理解与掌握，并能很好地运用。整个“砸”三角形和长方形的过程中，相互对比，恰到好处地处理了“教”与“学”的关系，学生在教师的引导下，有效地思索猜想，在活动中获得数学知识的同时，感悟了数学思想，积累了活动经验，培养了学生思维条理性和严密性，发展了空间观念。

三、谁有不一样的想法？

“有一千名读者，就有一千个哈姆雷特。”每个人所处视角或思考角度的不同，对同一问题会产生不同的看法，所以数学课堂的教学，教师应多问“谁有不一样的想法？”轻盈的一问会“钓”出让人惊喜的“大鱼”。谈不一样是对他人看法的补充，是对他人看法的质疑，是对他人看法的辩驳，只有说出来自己和别人不一样，思维上的印迹会更加清晰与牢固。培养学生在学习上敢于提问、质问、疑问、责问，在其“问”下，会有新的问题产生，使学习得以继续与深入，通过学生提出自己的问题，使思维得到了外化，使自己得到与别人接收的描述表征清晰有度。苏教版四年级下册《三角形内角和》教学，通过师生共同创设情境，引发冲突，以疑促思，寻求验证，最后得出不同形状的三角形内角和都是180°。

师：刚才我们接触的是测量法，但通过我们实地检测，有时候测量不够准确，这个结论不科学。谁有不一样的想法呢？

生1：我是将三角形的三个内角向形内折叠，这三个顶点交在一起，角的两边分别重合，就形成一个平角，平角是180°，说明三角形的内角和是180°。（生一边折叠一边解释）。

生2：我的方法更简单，我是先画一个平角，然后把这三个角分别剪下来，这样沿着平角一个一个地拼在一起，正好与平角重合。这验证了我的猜想：三角形內角和是180°。

师：折叠法和剪拼法比测量法科学有效。谁有不一样的想法？

生3：我的想法更特别一些。我把三角形的三条边分别延长成为平角（如图3），三个平角的和是：180°×3=540°，我把∠1、∠2、∠3分别剪下来拼在一起成一个周角，540°-360°=180°，也说明三角形内角和是180°。

生4：我的想法是：长方形的4个角都是直角，内角和是360°，现在沿着对角线剪开，把剪开后的两个三角形进行对比，发现两个三角形一样大小。也就是把360°平均分成2份，一份就是180°，也证明三角形内角和是180°。

学生是课堂教学的主体，引导学生主动探索解决问题的策略，激活学生的思维，让学生亲历知识产生的过程，通过自己语言和行为表征，把自己思维表征传递给其他同学，让他们在易解下形成自己的思维表征，从而使“授方”与“收方”都能体验到成功的快乐。

黎巴嫩诗人纪伯伦有诗云：我们已经走得太远，以至于忘记了为什么出发。要想不忘记出发的原因，就不能走得太远，在边行边走中，换一种思路去验证。认知心理学的观点表明：一个问题表征清楚，问题就解决了一半。“横看成岭侧成峰，远近高低各不同。”课堂上，教师多问、多暗示的操作演示比用语言描述更清楚……学生会将内隐的思维外显而可视，通过画图、操作等过程，使新旧知识不断分化重组，形成一个有意义的主动构建知识的过程。这个过程是对汲取的信息进行加工，重新组织若干已知规则，形成新的高级规则，用以达到一定的目标。所汲取来的将成为解决问题过程的思维素材，即问题解决有个适合自己的清晰思维表征形式，学生思维能力随之发生变化也即发展了学生的数学思维。