察题观式 事半功倍*
——以高三复习课“解三角形”为例谈解题效益
●王萍萍
(台州市第一中学,浙江 台州 318000)
察题观式 事半功倍*
——以高三复习课“解三角形”为例谈解题效益
●王萍萍
(台州市第一中学,浙江 台州 318000)
三角式的变换灵活而富于技巧,奇妙的公式变换体现了数学的统一与转化思想.然而也正因为公式太多、技巧性太强,使得很多学生对三角变换晕头转向、望而却步.文章对“解三角形”中的题目条件与结论作了探究,总结解题思路和解题规律,从而使学生提高解题技能与解题效益,达到事半功倍的效果.
解题方向;转化;正弦定理;余弦定理
1 问题提出
《2017年浙江省普通高考考试说明》中对解三角形的要求是:掌握正弦定理、余弦定理及其应用.在浙江省数学高考试题中,解三角形题型常被安排在解答题的第1题,用来考查学生的基本数学知识与能力.“良好的开端是成功的一半”,第1题能否顺利解答对学生考场心态影响很大.

1)求角A的大小;

(2015年浙江省台州市一模数学试题第16题)
(答案:1)60°;2)2.)
解答结果显示第1)小题的得分率为94%,第2)小题的得分率仅为52%.遵循高考的定位,命题者设计此题时,所考虑的解法(即下文思路1)很简洁、自然.笔者对学生的解答过程与方法作了调查,基于三角形的边角关系,第2)小题的解答大致有以下2个思路:
思路1 (化角为边)由于A=60°,a=1,根据余弦定理可得
b2+c2-bc=1,
从而
b2+c2=1+bc≥2bc,
即
bc≤1,
故


思路2 (化边为角)根据正弦定理可得

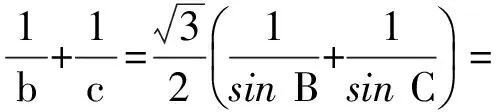
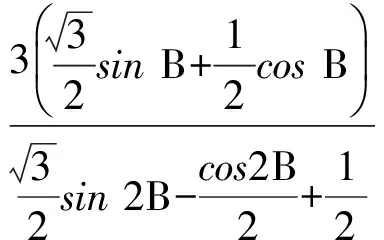
(1)
(能解答到这一步,需要考生具备一定的运算能力和坚毅的性格.)
对于式(1),有以下几种变形结果:
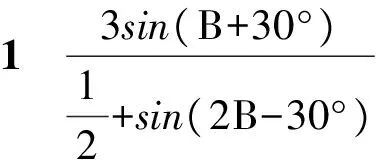



在这4个变形式中都出现了2个角的三角函数值,找出式中2个角之间蕴涵的内在联系是继续化解此题的关键.变形1、变形3和变形4中2个角之间的倍角关系非常隐秘,使得考生陷入迷惘的困境,而在变形2中不难发现其倍角关系,继而可变形得


把解题认为是纯粹的“智力活动”是错误的.决心和情绪也起了很重要的作用.决心会随着希望与无望、满意与沮丧而产生波动[1].思路2的思维链比较长,过程繁琐而曲折,不少考生因个人意志力薄弱而半途而废、浅尝辄止.其中不乏意志坚定且功底雄厚的学生,虽然获得最后结果,但在紧张的限时测试中消耗过多的时间着实可惜.
为什么这些考生不是按命题者预设的思路去解答,而是舍近求远?这种思维差距是什么原因造成的?我们知道并非所有的解三角形问题都适合“化角为边”,如何选择明智的解题方向使得解题效果事半功倍?笔者针对以上现象设计了一堂以解题效益为主题的高三复习课,让学生在亲历“一题多解”的过程中对解题思路、解题规律进行探索和总结,学会选择高效的解题方向,从而提高解题技能与效益.
2 教学目标
分析解三角形的类型与结构,应用正弦定理、余弦定理达到三角形边角之间的联系和转化,学会用数形结合的方法解决问题,提高解决综合问题的能力.
3 教学简录及说明
3.1 依托典型例题,完善知识网络

1)求角A的大小;
2)若a=3,sinB=3sinC,求b,c的值.

3.2 放手一题多解,绽放各种思维
3)若a=3,求bc的范围.

图1


即

显然当动点A运动到点M处时,AM达到最大值(此时B=C=60°);当动点A靠近端点B,C时,AH接近于0(此时B→120°,C→0°或B→0°,C→120°).
有了这种定性的感知,学生能够比较自然顺畅地进行数的运算推理.课堂生成片段如下:
思路1 (化角为边)由于A=60°,a=3,根据余弦定理可得b2+c2-bc=9,即
b2+c2=9+bc≥2bc,
从而
bc≤9,
故
bc∈(0,9].
思路2 (化边为角)根据正弦定理可得
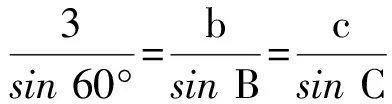
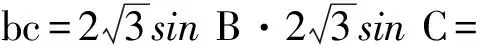
12sinB·sin(120°-B)=
6sin(2B-30°)+3.
因为B∈(0°,120°),所以2B-30°∈(-30°,210°),故bc∈(0,9].
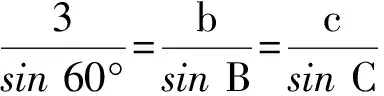
3.3 巩固经验之法,加深本质认识
4)若a=3,求b+c的范围.
设计说明 人们总是自然地想着去重复使用过去在类似的情况下已获得成功的那些方法[3].有了第3)小题的经验,学生很容易从常规角度去思考,去解题.课堂生成片段如下:

图2
学生先在圆中进行定性判断:如图2,当动点A运动到点M处时,b+c达到最大值(此时B=C=60°);当动点A靠近端点B,C时,b+c接近于3(此时B→120°,C→0°或B→0°,C→120°).
思路1 (化角为边)由于A=60°,a=3,根据余弦定理可得
b2+c2-bc=9,
从而
b2+c2=9+bc≥2bc,
即
bc≤9,
于是
(b+c)2=9+3bc≤36,
因此
b+c≤6.
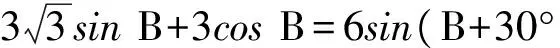
由于B∈(0°,120°),即B+30°∈(30°,150°),从而
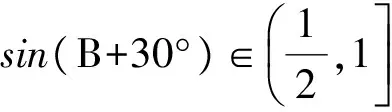
故
b+c∈(3,6].
思路3 (方程思想)本题等价于“已知b2+c2-bc=9,求b+c的范围”,其实质是“已知二元条件,求二元函数的值域”的问题,常规思路是代入消元转化成求一元函数的值域.在二次方程式b2+c2-bc=9中直接用b表示出c比较繁琐,因此可令b+c=t,将c=t-b代入方程b2+c2-bc=9,得到关于b(视次元t为参数)的一元二次方程3b2-3tb+t2-9=0有正实数解,从而
解得
b+c∈(3,6].
评注 采用思路1的学生能轻松得到“b+c≤6”的结果,但这也是利用不等式求解的一个瑕疵,只能得到范围的一端,在这里若是在解题之前有过定性的判断,不难根据“三角形两边之和大于第三边”的性质而补上限制条件“b+c>3”,可谓“亡羊补牢,为时未晚”!若题目只求最大值,则思路1不失为思路明晰且计算简洁的上上之策.
3.4 遭遇解题挫折,反思条件与结论

图3
5)若a=3,且△ABC为锐角三角形,求b+c的范围.
设计说明 此题虽然表面上看上去只比第4)小题加了对角的限制,然而第4)小题的思路1与思路3在这里却无法施展.课堂生成片段如下:

由第4)小题的思路2可知
b+c=6sin(B+30°).
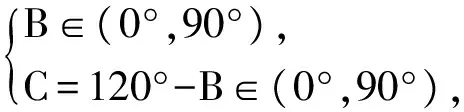
B+30°∈(60°,120°),
从而
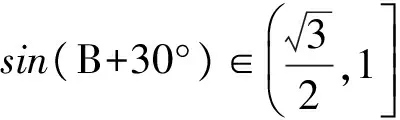
故
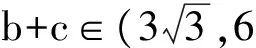

3.5 提高能力要求,驱动转化思想
6)若角C为钝角,且a+b=pc,求实数p的取值范围.

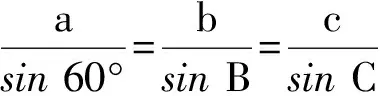

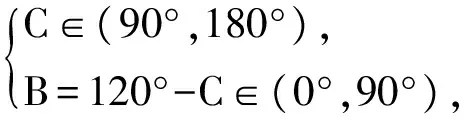

从而
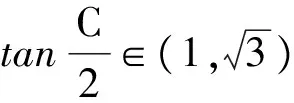
故
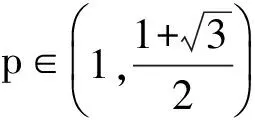
评注 作为高三学生,拿到一道题目不仅要了解有几种方法,更应该知道这些解法的根源在哪里、优劣性在哪里,只有这样才能有效选择解题方向,提高解题效益,运筹于帷幄之中.
3.6 提炼解法规律,总结数学思想
对于解三角形的问题,基本思想是“统一”,一般2种思路都可行,主要是通过正弦定理与余弦定理,将已知条件或统一到边上或统一到角上,再结合有关公式解决.解题中除了要选择自己擅长的方法,更重要的是学会“察题观式”,灵活选择,机智处理,养成良好的解题习惯.
步骤1 面对条件和结论联系相关公式;
步骤2 结合图形进行分析;
步骤3 预测思路,选择恰当途径.
一般来说,若是条件给出的是“关于边的限制条件”,或是较容易可转成“关于边的限制条件”,则例1的思路1不失为一种快捷有效的方法;若是条件给出的是“关于角的条件限制”,或者不容易转化成“关于边的限制条件”,则例1的思路2较为适宜.
4 反思与回顾
高三复习课的首要任务是把学生先前学的知识连成线、铺成面、织成网,从而实现融会贯通,这就需要教师站在思想方法的高度进行解题教学,不论题目如何千变万化,自然可以做到游刃有余.所谓“不畏浮云遮望眼,只缘身在最高层”,经过这一课的学习与总结,学生再来反思文首的例1,思路1的优势不言而喻.
[1] 波利亚.怎样解题[M].涂泓,冯承天,译.上海:上海科技教育出版社,2007.
[2] 王弟成.教师深度引领 学生高位发展[J].数学通报,2015(1):22-26.
[3] 波利亚.数学的发现[M].刘景麟,曹之江,邹清莲,译.北京:科学出版社,2006:67-68.
�2017-01-20;
2017-03-03
王萍萍(1983-),女,浙江台州人,中学一级教师.研究方向:数学教育.
O123.1
A
1003-6407(2017)08-10-04

