对2017年全国卷理科第20题的解法探究与拓展*

●凡胜富 (阜阳市第三中学,安徽 阜阳 236000)

●蒋 娟 (阜阳市颍泉小学,安徽 阜阳 236000)



对2017年全国卷理科第20题的解法探究与拓展*

●凡胜富 (阜阳市第三中学,安徽 阜阳 236000)

●蒋 娟 (阜阳市颍泉小学,安徽 阜阳 236000)

圆锥曲线定点问题是高考中一个热点问题.由于运算能力要求高、综合性强，也是学生比较惧怕的问题之一.文章通过对一道高考题的解法分析，引导学生进行审题，如何进行解题方法的选择、思考视角的选择、以及对试题的拓展.

切入点；特征；几何关系；推论

1 题目呈现，理清思路

1)求C的方程；

2)设直线l不经过点P2且与C相交于点A,B，若直线P2A与直线P2B的斜率之和为-1，证明：l过定点．

(2017年全国数学高考新课标卷理科试题第20题)

分析 这是一道经典的圆锥曲线定点问题，其考查的知识涉及解析几何的重点内容.通常借助方程的思想进行分析、解答，利用解方程或根与系数的关系求解，同时通过灵活利用图形的几何特征及代数表达式的特征逐步优化，这类试题的综合性和灵活性较强.

2 挖掘条件，分析解答

视角1 由线切入，寻找几何关系

证法1 (从直线PA，PB入手，求出直线AB的方程)设直线P2A:y=k1x+1，P2B:y=k2x+1，且k1+k2=-1,联立方程组

得

从而

同理可得

于是直线AB的斜率为

因此直线AB的方程为

即

亦即

故直线l过定点(2,-1).

评注 注意到点P2的坐标为(0,1),故从直线P2A与P2B的方程切入，求出点A,B的坐标，再通过两点求出直线方程，从而确定定点.解题过程中利用k1+k2=-1，把式中括号部分均转换为只含参数k1，目的是把方程转化为点斜式形式，给化简指明方向.

证法2 (直接从直线AB入手，寻找参数k和b的关系) 1)当直线l的斜率不存在时，设l:x=m,A(m,yA),B(m,-yA),则

得m=2，此时l过椭圆的右顶点，不存在两个交点，故不满足题意．

(1+4k2)x2+8kbx+4b2-4=0,

从而

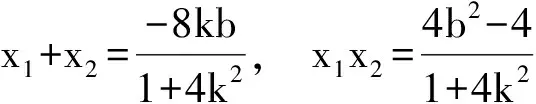
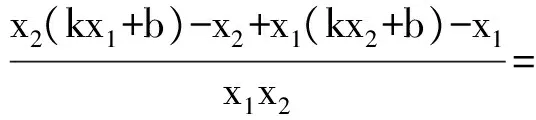
又b≠1，得b=-2k-1，此时Δ=-64k，即存在k<0，使得Δ>0成立．因此直线l的方程为

y=kx-2k-1=k(x-2)-1，

当x=2时，y=-1，故l过定点(2,-1)．

评注 证法1利用点A,B坐标来求直线AB的方程，运算量较大；证法2直接设直线AB的方程，联立方程组，通过对A,B的坐标设而不求来表示直线P2A与直线P2B的斜率的之和为-1，从而得到两个变量的关系来确定定点.

证法3 (利用点A,B,M共线进行优化)设直线P2A:y=k1x+1，P2B:y=k2x+1，且k1+k2=-1,联立方程组

得

从而

同理可得

假设直线l过定点M(a,b)，由于点A,B,M共线，从而

恒成立.又因为k1+k2=-1，所以

评注 考虑到证法1利用A,B坐标求出直线AB的方程，所得直线方程形式复杂不易得到定点，于是通过点A,B,P2共线这种几何关系来优化，从而得到恒等式，利用对应部分系数相等，得到定点坐标.

视角2 由点切入，寻找几何关系

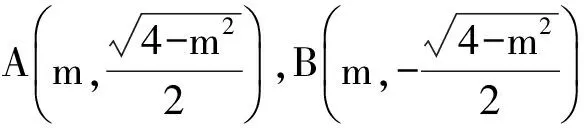
解得m=2，此时A(2,0)，B(2,0)不合题意.

当直线l的斜率存在时，设直线l的方程为y-n=k(x-m)，其中n-km≠1,A(x1,y1,),B(x2,y2)，由

得 (1+4k2)x2+8k(n-km)x+4[(n-km)2-1]=0.

由Δ>0，可得

4k2-(n-km)2+1>0,

从而

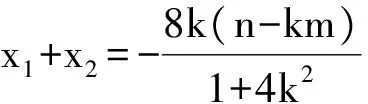
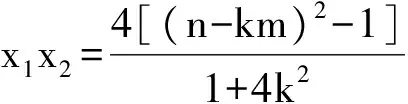
又直线P2A与直线P2B的斜率之和为-1，得

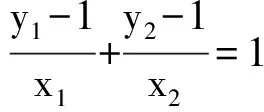
即

亦即 (2k+1)x1x2+(n-km-1)(x1+x2)=0,

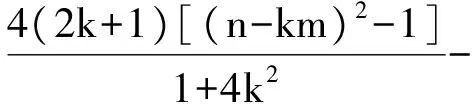
化简得 (n-km-1)[(2-m)k+1+m]=0.

因为n-km≠1，所以

(2-m)k+1+n=0，

又m,n是定值，k是变量，得

2-m=0, 1+n=0，

解得m=2,n=-1,故直线l过定点(2,-1).

评注 从隐定点切入，通过定点在直线上，反设直线AB的方程及点A,B的坐标，再利用直线P2A与直线P2B的斜率之和为-1，建立等式，求出定点坐标.

证法5 (从点A,B入手，利用代数式特征进行优化)设A(x1,y1)，B(x2,y2),因为点A,B,P2均在椭圆上，所以

(1)

(2)

式(1)-式(2)得

(x1+0)(x1-0)+4(y1+1)(y1-1)=0,

即

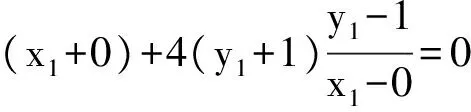
亦即

(x1-0)+4(y1-1)kP2A+8kP2A=0,

从而

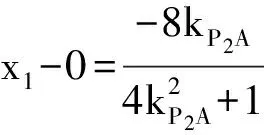
同理可得

设直线l过定点M(m+0,n+1)，则

恒成立，即

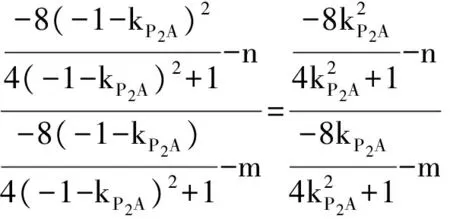
因为上式恒成立，所以对应系数相等,可得：m=2,n=-2，故直线l过定点(2,-1).

评注 从点A,B的坐标切入，利用A,B在椭圆上其坐标满足椭圆方程，利用代数式特征来构造直线P2A与直线P2B的斜率形式，再通过巧设定点坐标M(m+0,n+1),使得运算量减少.

3 探究本质，推广结论

解题重在解，贵在思，解答题目本身是表象，推广、提升才能真正体现命题人的意图，才能提高解题能力和效率.那么，上述问题能否推广到一般的椭圆呢？答案是肯定的.

证明 设直线l1的斜率为k，则l2的斜率为m-k，依题意知k存在，设直线l1的方程为

y=k(x-x0)+y0，

且l1与椭圆交于点A(x1,y1),设直线l2的方程为

y=(m-k)(x-x0)+y0，

且l2与椭圆交于点B(x2,y2).因为P(x0,y0)，A(x1,y1)在椭圆上，所以

两式相减得

即

亦即

消去x1，得

从而

同理可得

由结论1可以推导出以下两个推论：

4 理想类比，延伸结论

基于上面的分析，此题还可以作以下推广和延伸：

5 结束语

通过对上述结论的探究，我们进一步认识到椭圆、双曲线、抛物线等曲线，除了自身存在一定的规律性外，圆锥曲线之间也存在一定的规律性[1]，需要认真研究试题，发掘其真正的内含，探索出新的规律性结论，并用于教学中，才可以真正深化思维，优美解法，提升解题效率.

[1] 徐永强.对一道圆锥曲线问题的探究与拓展[J].中学数学，2016(9):87-88.

�2017-06-15；

2017-07-03

凡胜富(1980-)，男，安徽阜阳人，中学一级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)08-44-04