一道课本例题的解析、改编与变式*

●李旺强

(清水县第六中学，甘肃 清水 741499)



一道课本例题的解析、改编与变式*

●李旺强

(清水县第六中学，甘肃 清水 741499)

例题讲解是数学课堂教学中必不可少的环节.文章中执教教师对课例进行深入的挖掘，使其在引领本节所学知识应用的同时，通过题型的改编、变式以及与高考试题的对应衔接来进一步开阔学生的视野，提升学生的思维能力.

一题多解；题型改编；变式提升

人教A版《数学(必修2)》第2.2节“ 直线与平面平行的判定”，笔者在讲授这一判定在具体问题中的应用时选用了课本上的例1作为示例，先让学生自己审题、寻找解决方法，培养学生动手动脑的习惯以及分析问题、解决问题的能力，同时增强他们的数学语感，积累解题经验.在让学生上台展示解法时，有学生提出了自己的见解与证明方法，针对学生的提议，笔者课后对其解法进行了归纳分析，并将课本例题进行了改编，同时增加了几道相同或相似背景的变式题，以提高学生对直线与平面平行的判定定理的理解和应用.

例1 求证：空间四边形相邻2条边的中点的连线平行于另外2条边所确定的平面.

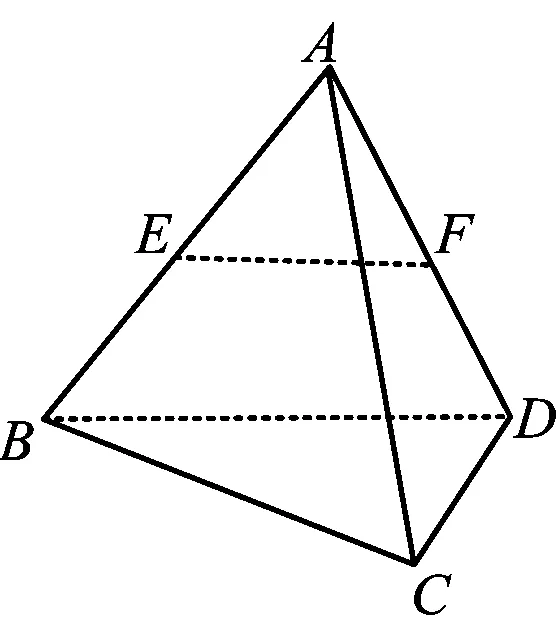
图1

已知：如图1，在空间四边形ABCD中,E,F分别是AB,AD的中点，求证：EF∥平面BCD.

(人教A版《数学》第55页例1)

该题涉及线段中点、平面几何的相关性质以及空间几何体等相关内容，主要考查学生对线面平行判定定理的理解与应用.通过此题的解答,掌握一些处理线面平行问题的相关思想和方法，重点考查学生的抽象能力和灵活处理立体几何问题的能力.

1 多视角探析

1.1 利用中位线定理改编

证法1 联结BD.因为E,F分别是AB,AD的中点，所以

AE=EB,AF=FD,EF∥BD.

又因为EF∥平面BCD，BD⊂平面BCD,所以

EF∥平面BCD.

评注 此证法直接借用题目已知条件，针对空间四边形的几何体结构，借用三角形中位线定理证明，简单、明了.

改编1 如图2，在空间四边形ABCD中,G是CD的中点，E,F分别是AB,AG的中点，求证：EF∥平面BCD.

分析 由题意易证EF是△ABG的中位线.

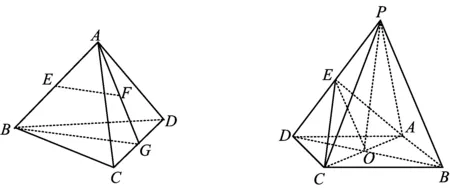
图2 图3

改编2 如图3，在底面为平行四边形的四棱锥P-ABCD中,点E是PD的中点，求证：PB∥平面AEC.

分析 联结BD交AC于点O,联结OE,则OE是△PDB的中位线.

变式1 如图4，已知E,F,G,M分别是四面体的棱AD,CD,BD,BC的中点，求证：AM∥平面EFG.

分析 联结MD交GF于点H，易证EH是△AMD的中位线.

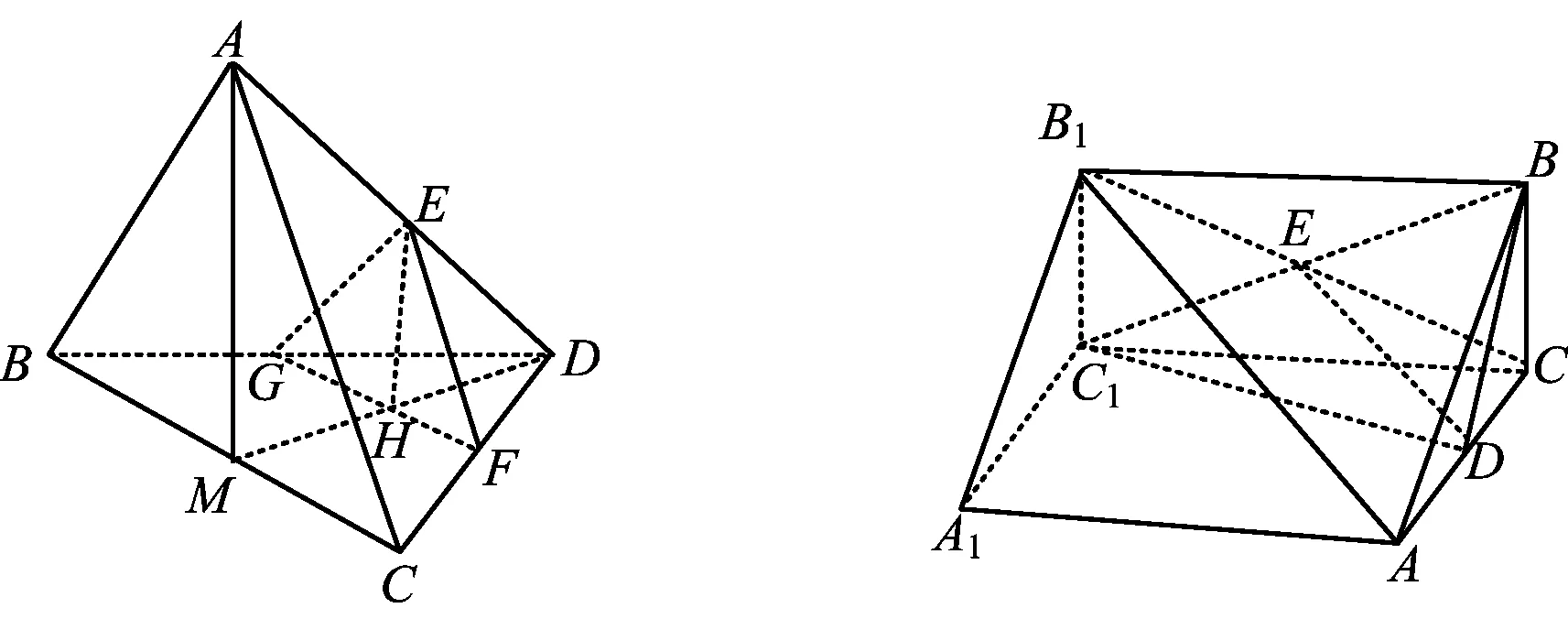
图4 图5

变式2 如图5，在三棱柱ABC-A1B1C1中，D为AC的中点,求证：AB1∥面BDC1.

分析 联结B1C交BC1于点E，易证ED是△B1AC的中位线.

高考联结1 如图6，在四棱锥P-ABCD中，底面ABCD为平行四边形，O为AC中点，M为PD中点，证明：PB∥平面ACM.

(2011年天津市数学高考文科试题第17题)

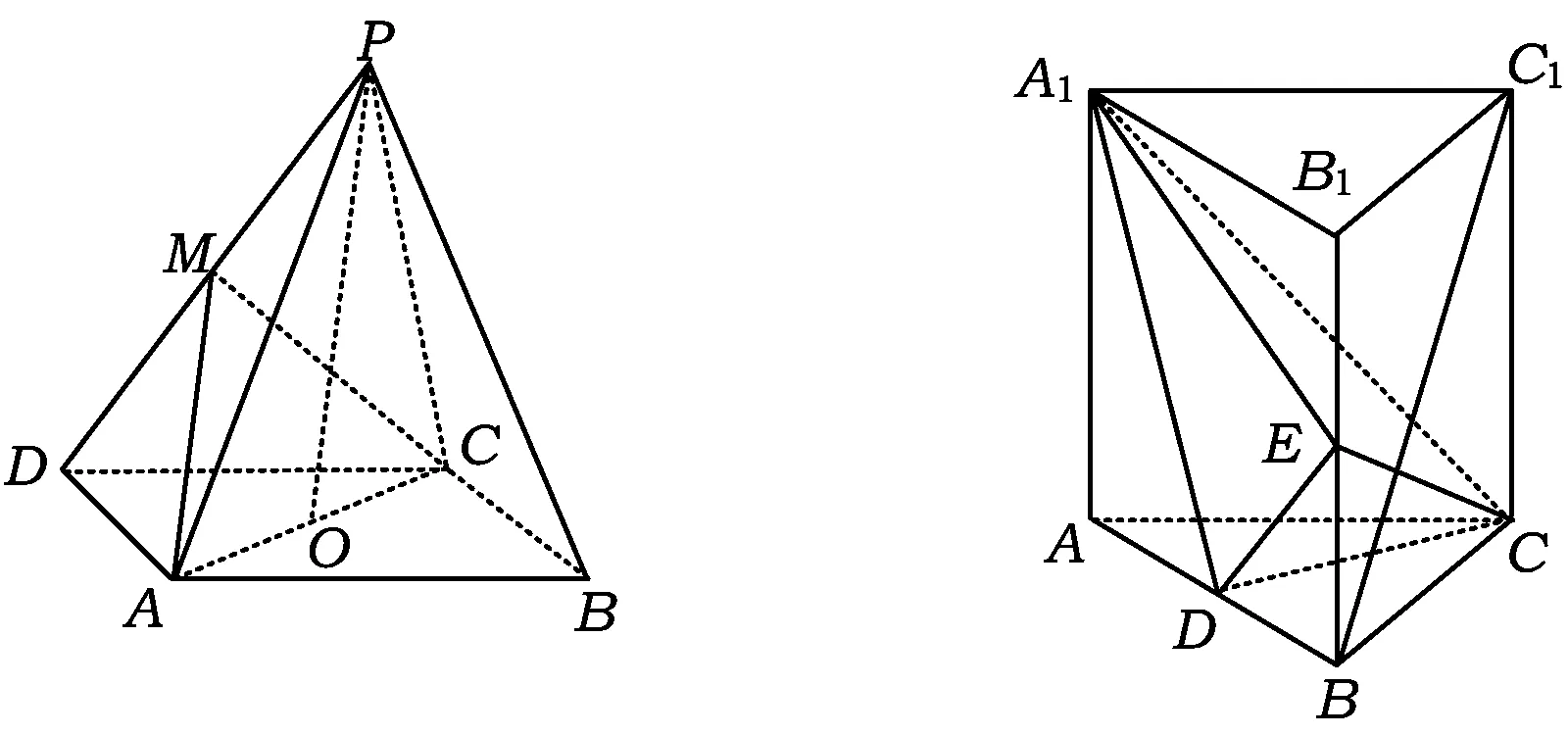
图6 图7

高考联结2 如图7,直三棱柱ABC-A1B1C1中,D是AB的中点，证明:BC1∥平面A1CD.

(2014年全国数学高考新课标卷Ⅱ文科试题第18题)

1.2 构造平行四边形或梯形改编

证法2 如图8，设G,H分别是BC,CD的中点，联结BD，EG,GH,FH,则

EF,

从而

EFGH,

故四边形EFGH是平行四边形.因为GH⊂平面BCD,所以EF∥平面BCD.

评注 该证法从已知条件“E,F分别是AB,AD的中点”出发，分别选取的中点G，H,采用构造平行四边形的方式进行了证明，虽然有点走弯路，但也是一种解决办法.

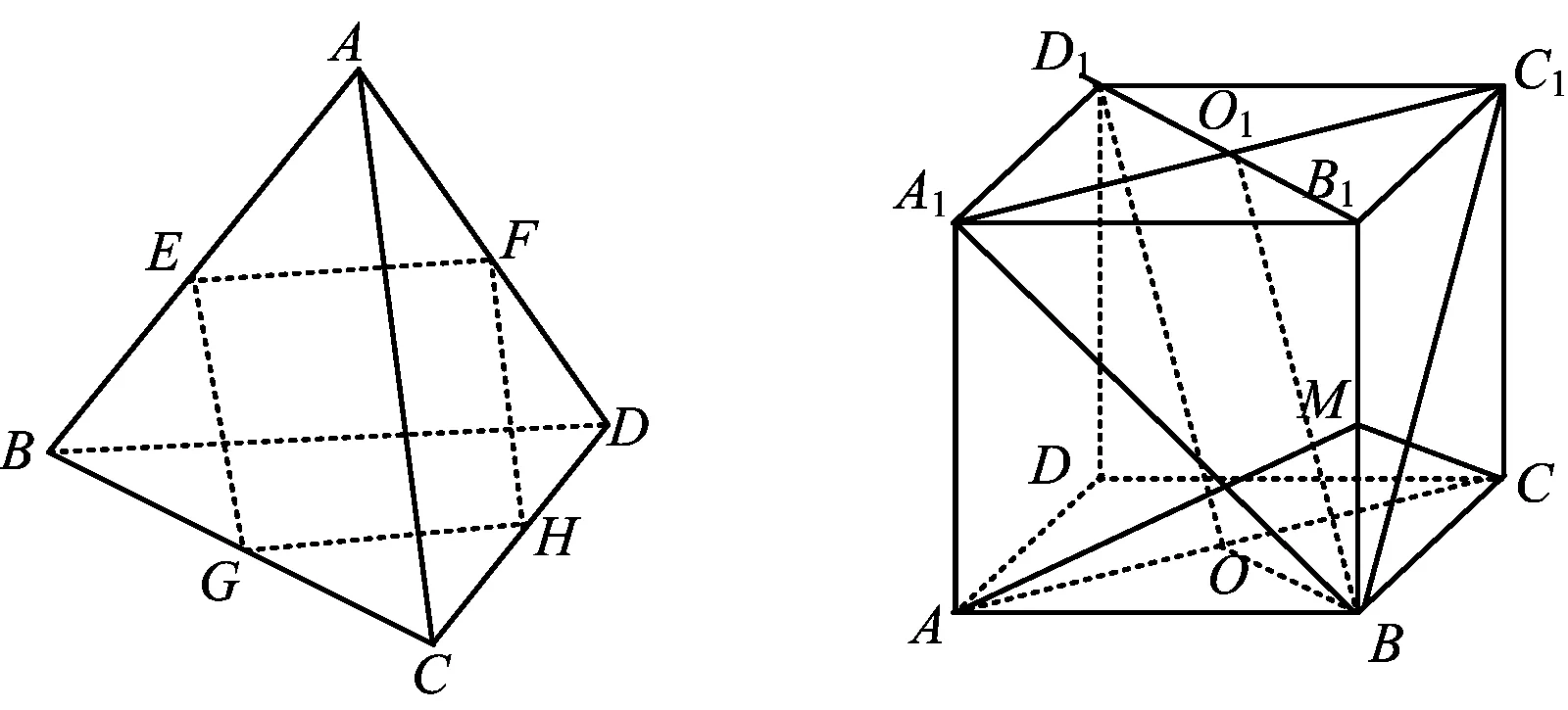
图8 图9

改编1 如图9，在正方体ABCD-A1B1C1D1中，O为正方形ABCD的中心，M为BB1的中点,求证：D1O//平面A1BC1.

分析 联结D1B1交A1C1于点O1,联结O1B,OB，易证四边形OBO1D1是平行四边形.

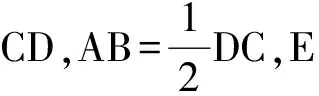
分析 取PC的中点F，联结EF，则易证四边形ABFE是平行四边形.

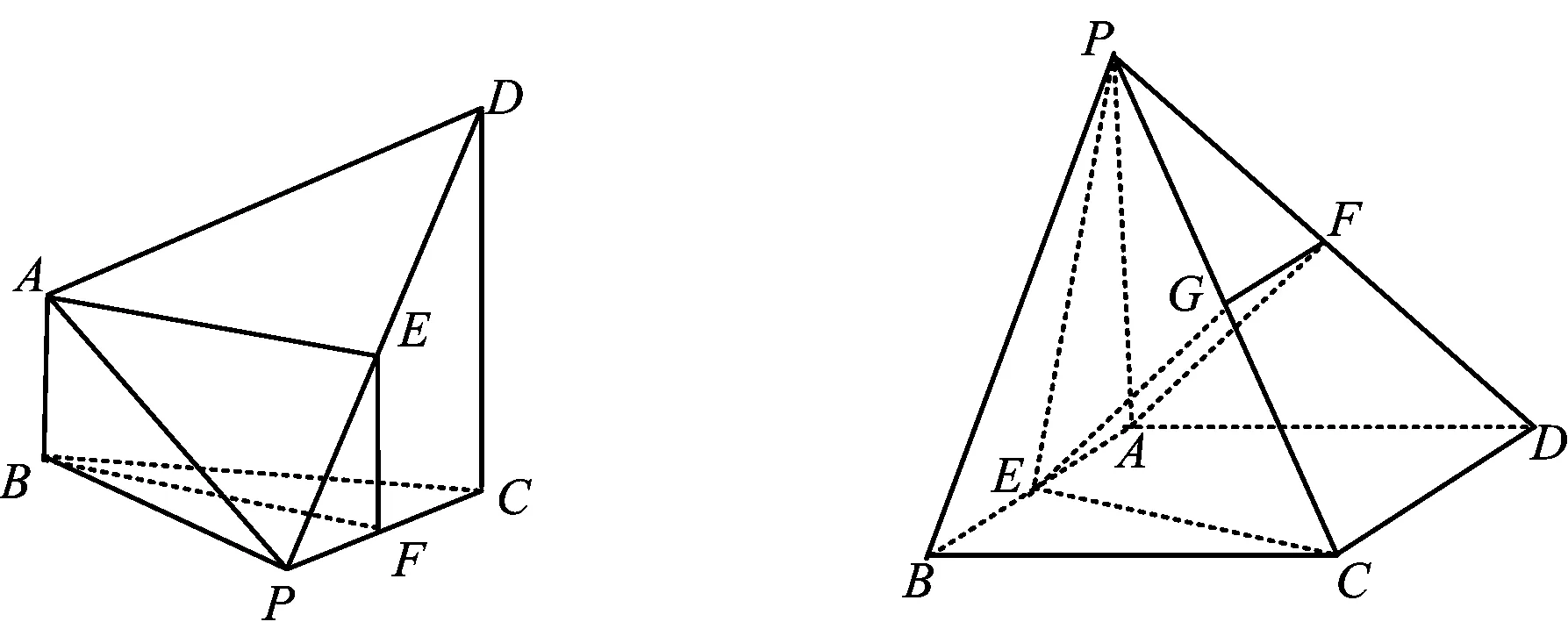
图10 图11

变式1 如图11，四棱锥P-ABCD的底面是平行四边形，点E,F分别为棱AB,PD的中点,求证：AF∥平面PCE.

分析 取PC的中点G，联结EG，FG，则易证四边形AEGF是平行四边形.

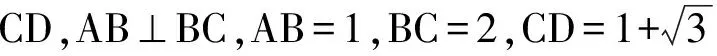
分析 取DB的中点H，联结GH,HC，则易证四边形FGHC是平行四边形.

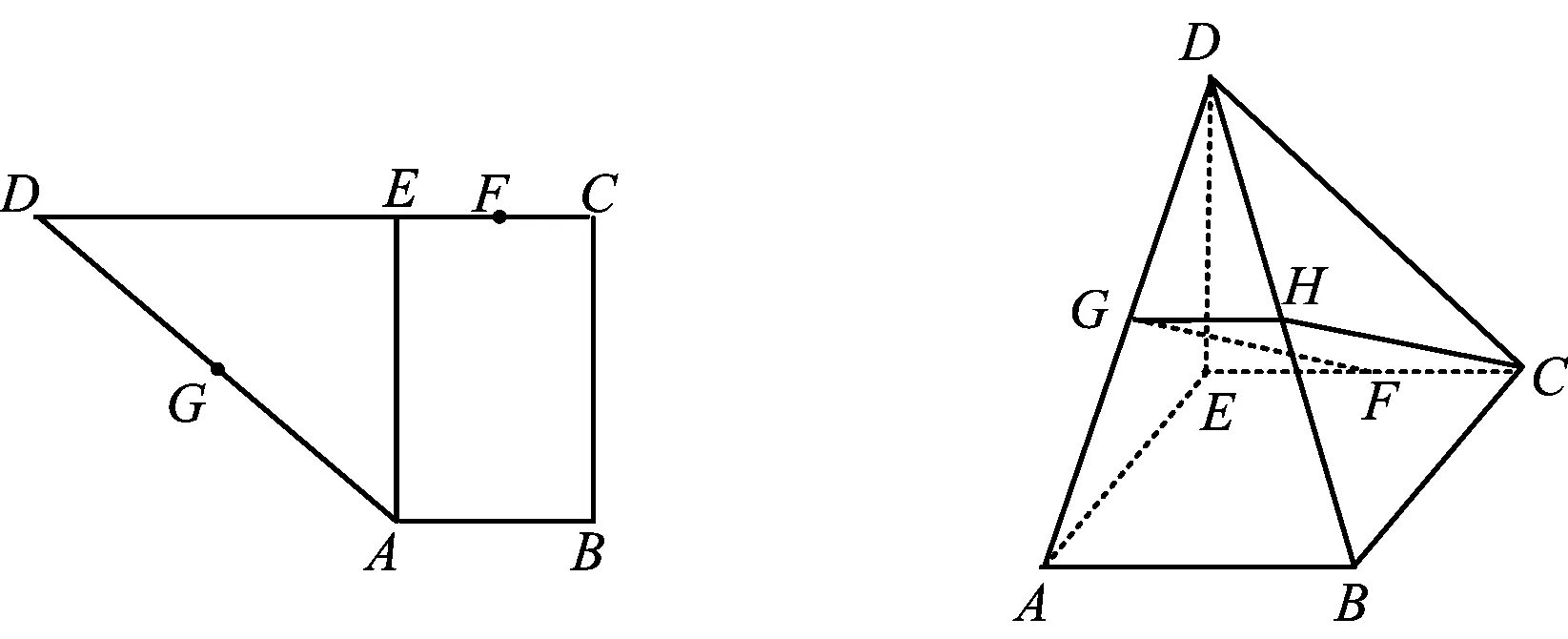
图12

高考联结1[1]如图13，在五面体ABCDEF中，点O是矩形ABCD对角线的交点，面CDE是等边三角形，棱EF，证明：FO∥平面CDE.

(2011年天津市数学高考理科试题第19题)

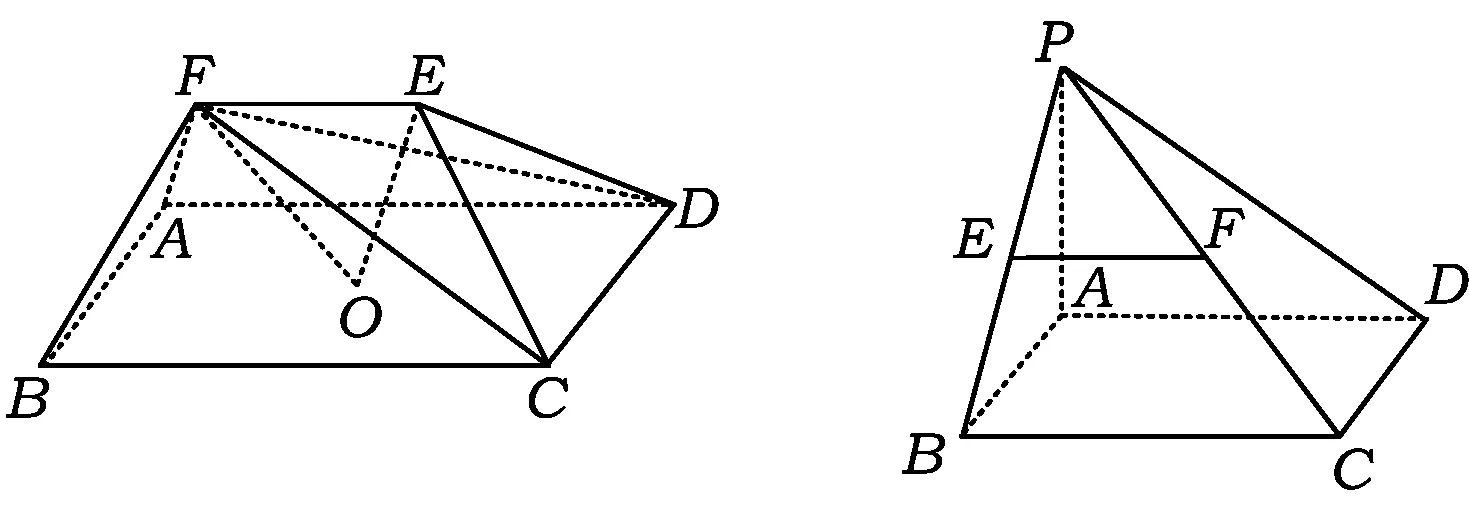
图13 图14

高考联结2 如图14，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，AP=AB，BP=BC=2，E，F分别是PB,PC的中点.

1)证明：EF∥平面PAD；

2)若H是AD的中点，证明：EA∥平面PHC.

(2010年陕西省数学高考文科试题第18题)

1.3 利用对应线段成比例改编

证法3 如图15，不妨设G是BC边上一点,过点G作GH∥BD交CD于点H,则四边形EGHF为梯形，从而

EF∥GH.

因为GH⊂平面BCD,所以

EF∥平面BCD.

评注 证法3直接观察让人有点匪夷所思，证法1可以说是简单、直接、省事，是首选方法.可为何放着现有的平行线不用却要画蛇添足重新来做呢？仔细琢磨，证法3隐含了另一种题型的证明方法，如将题目中的已知条件改成边之间的比例关系，或者涉及相似三角形等相关知识时，证法3大有用场.

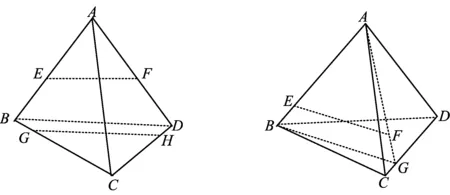
图15 图16

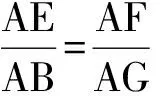
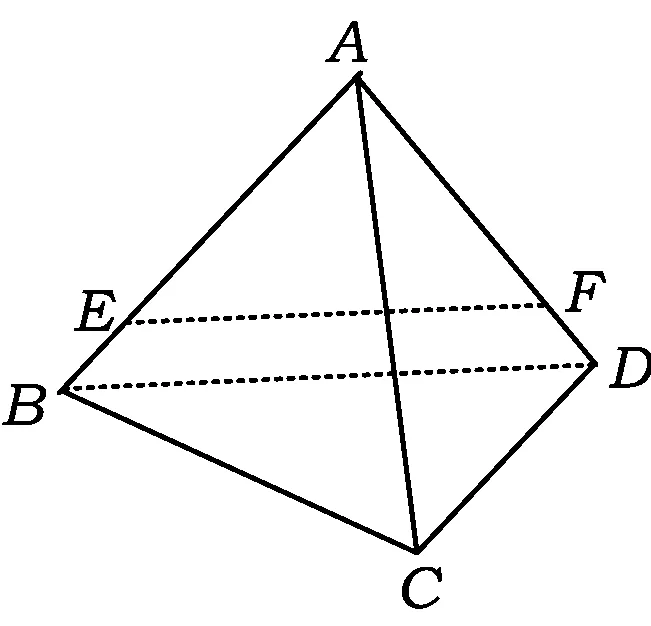
图17

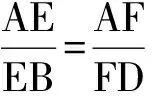
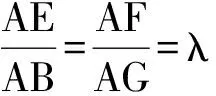
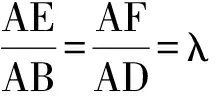
2 逆向思维、沟通迁移

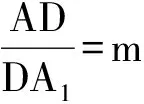
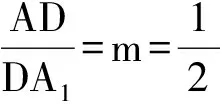
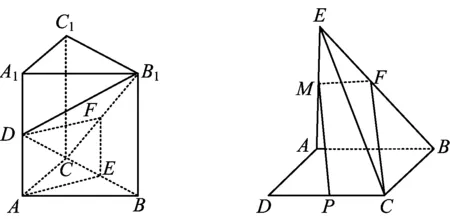
图18 图19

例3 如图19，四边形ABCD为正方形，△ABE为等腰三角形，AB=AE,P是线段CD的中点，问：在直线AE上是否存在一点M,使PM∥BCE平面？若存在，请指出点M的位置，并证明你的结论.

分析 过点M做MF∥AB,联结CF,则当四边形PCFM为平行四边形时,PM∥平面BCE，故M是AE的中点.

学生是一个个鲜活的个体，对待问题有一定的思想和灵感.通过例1的解法展示可以看出学生对线面平行的判定理解得比较深刻，在具体问题应用时，能够抓住本质进行必要的构造，解题思路清晰、新颖，有自己独特的见解.再通过改编题使学生对线面平行的判定理解更为深入，应用更加灵活、恰当，同时也拓展了学生的思维，开阔了学生的视野.

3 结束语

改编题分别体现了相同(相似)背景下、不同背景下问题的求解策略，有效地刺激了学生的空间想象能力，也激发了他们的探究热情，调动了他们学习的积极性和兴趣性，使数学在他们内心中趋于有趣化、常态化.一道课本例题的解析、改编与变式使他们对本节知识的理解更加透彻[2]，使他们的思维随着试题的改编、变式而呈螺旋式上升，让课例发挥了应有的功能和作用.

[1] 李旺强．数学教学中“讲”的再认识——对一个向量问题教学的思考[J].中学教研(数学),2016(9)：7-9．

[2] 曹凤山.从课本例(习)题到高考题的若干命题途径.[J]中学教研(数学),2012(1)：26-28．

�2016-12-10；

2017-01-15

李旺强(1982-)，男，甘肃清水人，中学二级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)08-27-03