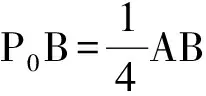1个公式 5类问题 14年高考*
——对角线向量定理在浙江高考中的妙用
●吴淑芳 朱成万
(杭州第十四中学,浙江 杭州 310006)
1个公式 5类问题 14年高考*
——对角线向量定理在浙江高考中的妙用
●吴淑芳 朱成万
(杭州第十四中学,浙江 杭州 310006)
浙江省数学高考试题有自己的风格和特点,常考常新,每年总有1~2道试题能被同一对角线向量定理秒杀.文章对该定理的应用进行分类解析,形成通解通法,实现从复习到考试的软着陆.
对角线向量定理;通解通法;极化恒等式
浙江省数学高考自主命题,从2004年以来,已经成功地实现了软着陆,并形成了自己的特点和风格[1].对主干知识的考查每年从不同的角度设问,常考常新,推陈出新.笔者研究发现:这14年(2004~2017)的浙江省数学高考试卷中每年都有1~2道试题能被同一个公式秒杀,这个公式就是:
(1)
笔者称式(1)为对角线向量定理(文献[2]称之为四点向量定理,笔者认为把它叫做对角线向量定理更能体现该公式的特点).它可以用来破解高考试题中有关平面向量数量积问题和立体几何中的异面直线所成角、线面角以及二面角等空间角度问题,也可以破解立体几何中有关距离的问题和翻
折问题.
1 对角线向量定理
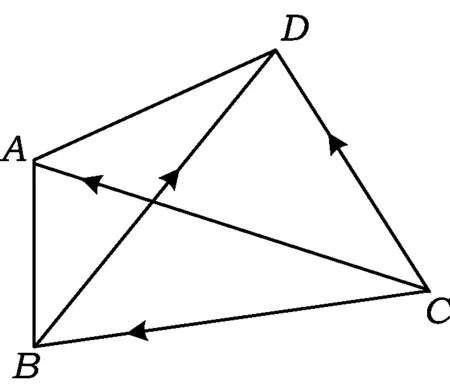
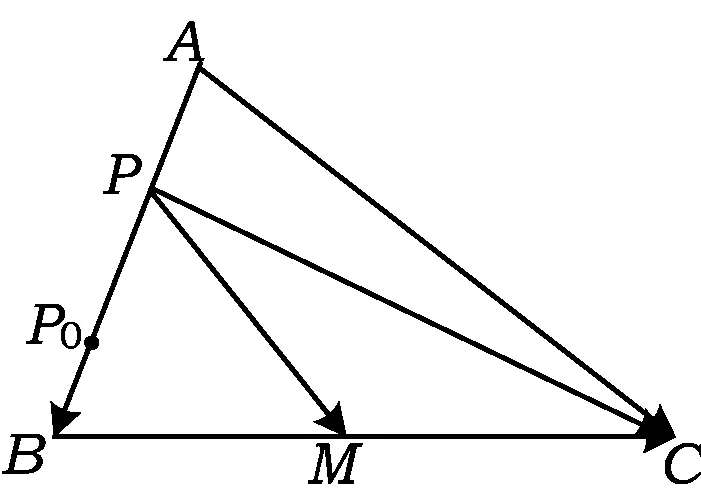
图1
如图1,在△ABC中,由余弦定理的向量式得
在△ADC中,同理可得

因此在四边形ABCD中,
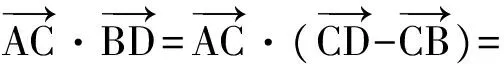
,

(1)
式(1)就是对角线向量定理,它表明:四边形的两条对角线对应向量的数量积可用4条边的长度表示.该定理的两个推论是显而易见的.
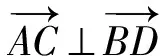
(2)
式(2)表明:当对角线互相垂直时,四边形两组对边的平方和相等.
推论2

(3)

图2
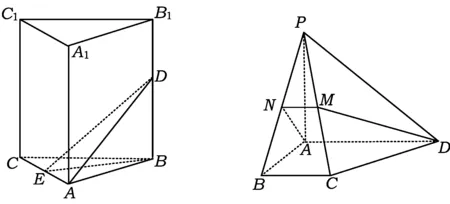
式(3)可以求平面或空间的角度问题,包括线线角、线面角和二面角.
需要说明的是,式(1)~(3)既适用于平面向量也适用于空间向量(如图2所示).
2 用对角线向量定理妙解浙江高考题
为了理解上的方便,笔者以知识内容为标准进行分类解析,从以下5个方面欣赏对角线向量定理在历年浙江省数学高考试题中的妙解.
2.1 用对角线向量定理妙解平面向量题
向量的数量积是向量中的一个重要问题,也是每年浙江省数学高考必考的核心内容之一.根据式(1),当四边形4条边的长度可控时(不要求4条边的长度都是已知的定值),就可以求对角线所在向量的数量积.

( )
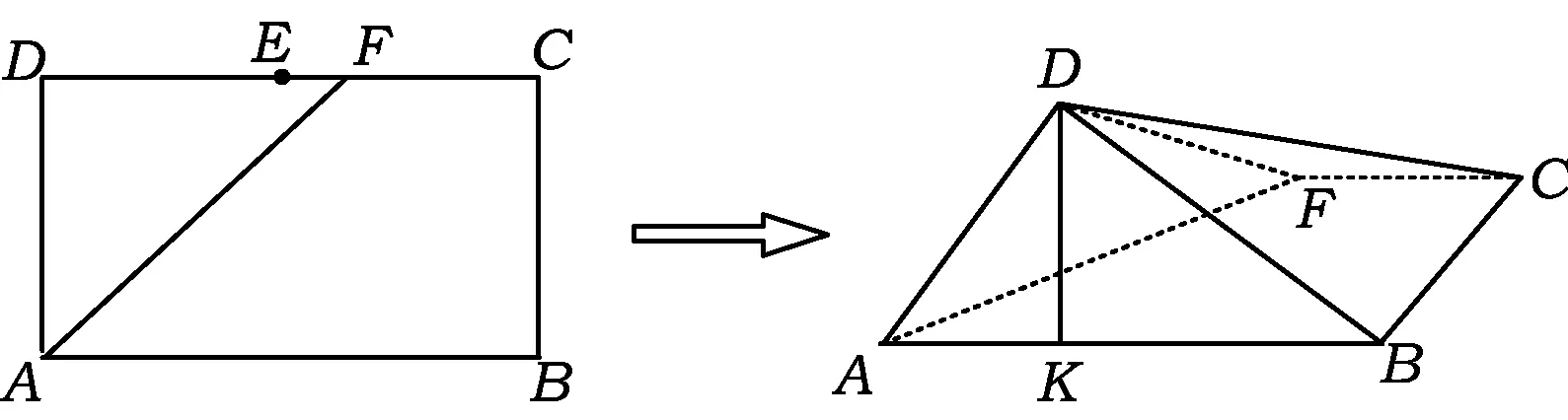
A.I1 C.I3 (2017年浙江省数学高考试题第10题) 解 由对角线向量定理得 所以I3 图3 图4 ( ) A.-8 B.-1 C.1 D.8 (2012年浙江省数学高考样卷第9题) 解 由对角线向量定理得 故选D. ( ) A.b2-a2B.a2-b2 C.a2+b2D.ab (2013年浙江省数学高考样卷第5题) 图5 图6 解 由对角线向量定理得 b2-a2. 故选A. 2.2 用对角线向量定理妙解线线角 求空间直线所成角通常有两种方法:一是作辅助线(平行线);二是建立空间直角坐标系,用坐标运算.利用推论2,可以很方便地求出两条异面直线所成角的余弦(避免了作辅助线和繁复的坐标运算).下面举两个例子,体会对角线向量定理在破解空间直线所成角问题中的威力. 例4 设M,N是直角梯形ABCD两腰的中点,DE⊥AB于点E(如图6).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则点M,N的连线与AE所成角的大小为______. (2005年浙江省数学高考理科试题第12题) 解 由题意得AM=EM.因为翻折后AB⊥面BCDE,∠AEB=45°,所以AN=EN.由对角线向量定理得 图7 例5 如图7,三棱锥A-BCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N分别是AD,BC的中点,则异面直线AN,CM所成角的余弦值是______. (2015年浙江省数学高考理科试题第13题) 解 容易求得 由推论2得 用向量法求线面角β:首先要找到平面的法向量n,再求法向量与所求直线方向向量的夹角θ,要注意角β与θ是互余的.用对角线向量定理求空间线面角的方法与步骤也是这样的,不过我们所用到的法向量,不必用坐标法求出,只需找平面的一条垂线段即可. 例6 在正三棱柱ABC-A1B1C1中,已知AB=1,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则α= ( ) (2004年浙江省数学高考理科试题第10题) 故选D. 图8 图9 例7 如图9,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,点M,N分别为PC,PB的中点. 1)求证:PB⊥DM; 2)求CD与平面ADMN所成的角. (2006年浙江省数学高考理科试题第17题) 1)证明 因为N是PB的中点,PA=AB,所以AN⊥PB.又AD⊥平面PAB,从而AD⊥PB,于是PB⊥平面ADMN.由DM⊂平面ADMN,知PB⊥DM. 2.4 用对角线向量定理妙解空间二面角 二面角是立体几何的重要内容,也是浙江省数学高考每年必考题目之一(特别是在立体几何的大题中).求二面角的大小通常需要建立空间坐标系,通过坐标运算求出法向量,进而求解;或者通过二面角的平面角定义作出平面角(这是一个难点).用对角线向量定理求二面角给出了一种全新的视角. 图10 1)求二面角A′-FD-C的余弦值; 2)点M,N分别在线段FD,BC上,若沿直线MN将四边形MNCD向上翻折,使点C与点A′重合,求线段FM的长. (2010年浙江省数学高考理科试题第20题) 2)略. 2.5 用对角线向量定理妙解立体几何翻折问题 用对角线向量定理破解翻折问题,可以通过代数运算来刻画边长与角度的变化,降低对空间想象能力的要求. 例9 如图11,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是______. (2009年浙江省数学高考理科试题第17题) 图11 解 因为面ABD⊥面ABC,又DK⊥AB,所以DK⊥面ABCF,故DK⊥AF.根据推论1可知:当DK⊥AF时, 设DF=x(其中x>1),则 x2+t2=12+[(x-t)2+1], 从而 ( ) A.存在某个位置,使得直线AC与直线BD垂直 B.存在某个位置,使得直线AB与直线CD垂直 C.存在某个位置,使得直线AD与直线BC垂直 D.对任意位置,直线“AC与BD”“AB与CD”“AD与BC”均不垂直 (2012年浙江省数学高考理科试题第10题) 显然AC与直线BD不垂直.而 当AC=1时,直线AB与直线CD垂直.故选B. 例11 如图12,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则 ( ) A.∠A′DB≤αB.∠A′DB≥α C.∠A′CB≤αD.∠A′CB≥α (2015年浙江省数学高考理科试题第8题) 图12 图13 所以 cos∠A′DB≤cosα, 即∠A′DB≥α.故选B. 评注 这是同一份试卷第二次出现此类问题. 图14 (2016年浙江省数学高考文科试题第14题) 解 翻折后仍有 设直线AC与BD′所成角为θ,由对角线向量定理得 当且仅当BD′最小时,AC与BD′所成角的余弦值最大. 设M是CD的中点,则 这就是极化恒等式,它可以由对角线向量定理推导而来,因此可将极化恒等式作为对角线向量定理的一个推论.从形式上看,极化恒等式揭示的也是向量数量积与对角线之间的关系[3]. ( ) A.∠ABC=90° B.∠BAC=90° C.AB=ACD.AC=BC (2013年浙江省数学高考理科试题第7题) 图15 解 如图15,取线段BC的中点M,则 对角线向量定理还可以秒杀更多的试题,限于篇幅,不再举例.研究用对角线向量定理秒杀一类浙江省数学高考试题,并不是追求高难度的解题技巧,相反,是寻求问题的通解通法,形成统一解法,着意于解题工具的选择,着意于数学问题的理解,直透问题的本质,看出题目的结果. [1] 高考数学研究组.浙江数学高考2004一路走来[M].杭州:浙江大学出版社,2016. [2] 范广发.用四点向量定理破解空间角难题[J].中小学数学:高中,2017(3):58-60. [3] 王红权,李学军,朱成万.巧用极化恒等式 妙解一类向量题[J],中学教研(数学),2013(8):24-25. �2017-06-15; 2017-07-03 吴淑芳(1978-),女,浙江东阳人,中学一级教师.研究方向:数学教育. O123.1 A 1003-6407(2017)08-36-05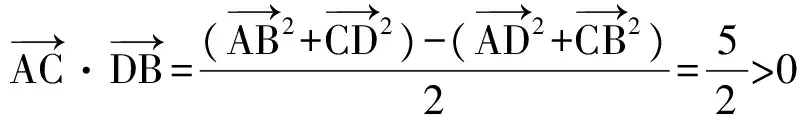






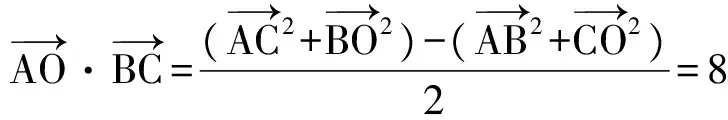










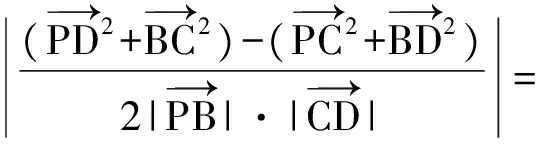









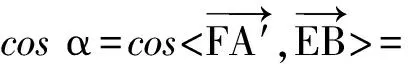








3 从对角线向量定理到极化恒等式