基础与能力并举 经典与创新共舞*
——2017年浙江省数学高考试卷评析
●郑日锋
(学军中学,浙江 杭州 310012)
基础与能力并举 经典与创新共舞*
——2017年浙江省数学高考试卷评析
●郑日锋
(学军中学,浙江 杭州 310012)
文章对2017年浙江省数学高考卷的特点、命题规律及命题的变化进行分析,指出试卷对教学的启示.
试题特色;文理合卷;核心素养;复习教学
2017年是浙江省高考改革后的第一年,较往年最大的不同是采用文理合卷.2017年浙江省数学高考试卷依然坚持“起点低、坡度缓、层次多、区分好”的命题思路和命题风格,严格遵循国家课程标准、省教学指导意见及省考试说明,充分考虑文理合卷,试题起点低,角度宽,既系统、全面地考查了高中数学的基础知识和基本技能,又多层次地考查了数学素养和学习潜能.试卷有较好的信度、效度与区分度,难度较前两年有所下降,有利于高校选拔人才,并对高中数学教学具有良好的导向作用,可谓“基础与能力并举,经典与创新共舞”.
1 试题特色
1.1 注重基础,体现人文关怀
试卷充分考虑到文理合卷的特点,从学科整体和思维价值的高度设计试题,体现人文关怀.试卷全面覆盖了中学数学教材中的主干知识模块,对数学基础知识的考查,既全面又突出重点,层次分明.命制的试题既让基础薄弱的学生可动笔,不致于望题兴叹,也让优秀学生感觉并不是那么容易,全卷没有偏难题,绝大部分试题入口宽,不同层次的学生会有不同的认识,但方法选择不当会导致耗时较多或出错.
立足课本.试卷中第1~4,6,7,11~14,18题以及第19题第1)小题、第20题第1)小题、第21题第1)小题,都来源于课本,或从课本中的例、习题直接改编而来,体现了数学试题的基础性.
考查概念.如第5题考查函数的极差,第6题考查等差数列的定义,第7题考查函数的单调性与导函数的符号的关系,解决这些试题只需概念清楚,无需多动笔.
降低起点.如第1~3,11,12,18题考查的知识点单一,考生如熟悉基本知识、基本方法,解决这些问题可以做到既快又对.
注重通法.试卷充分考虑了解题方法的大众化与常规化,不在冷僻的技巧上设置问题.努力贴近学生在通性通法上下功夫,大部分试题中规中矩、不偏不怪,材料背景熟悉,设问方式常规,解题方法基本,和平时教学匹配度高,在考基础、通性、通法上体现得浓墨重彩、淋漓尽致.同一个问题,可以有多个视角,进而可用多种方法,可以有效区分不同层次的学生的数学水平和能力,如第19题立体几何题既可用空间向量法解,也可用传统综合法解.
例1 已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是______,最大值是______.
(2017年浙江省数学高考试题第15题)
思路1 利用向量加减法几何意义及重要不等式,得
|a+b|+|a-b|≥2|a|,
|a+b|+|a-b|≥2|b|,
从而 |a+b|+|a-b|≥2max{|a|,|b|}=4,
当且仅当a,b共线时,等号成立,故|a+b|+|a-b|的最小值是4.由

思路2 利用向量的坐标表示及三角函数知识,设a=(1,0),b=(2cosθ,2sinθ),则
|a+b|+|a-b|=
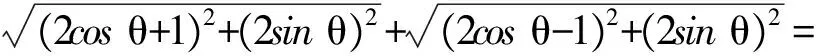

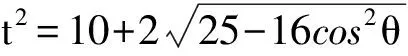
从而
16≤t2≤20,

设置台阶,选择题、填空题、解答题都分别由浅入深,每一道解答题分层设计,前一小题的解决为后面的小题作铺垫,逐步化解难点,拾级而上,即便压轴题也是如此.
1.2 能力立意,聚焦核心素养
试卷在考查数学基础知识和基本技能的基础上,注重数学思想方法、数学能力的考查,突出数学本质,检测学生的数学理性思维及数学核心素养.

(2017年浙江省数学高考试题第17题)
本题表面上是已知含参数函数的最大值,求参数的范围问题,本质是函数图像的对称性问题.
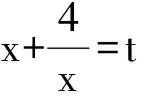
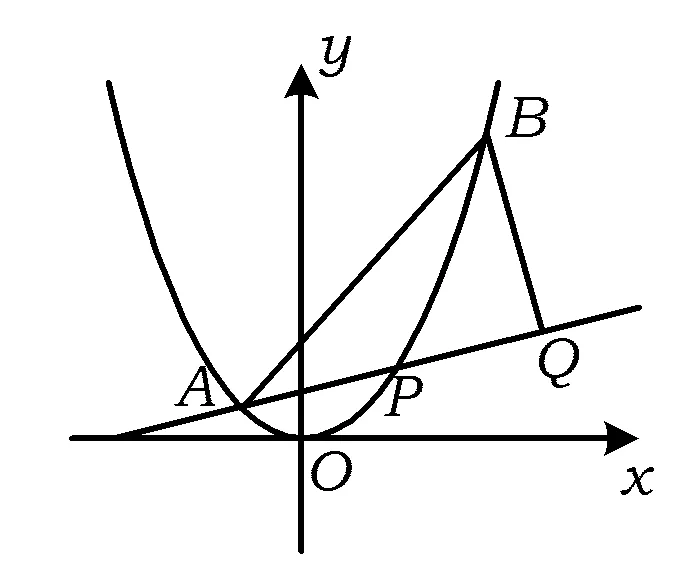
此方法需要学生运用观察、类比、化归的策略,考查了学生直观想象、数学抽象、数学建模等数学核心素养.解决此题还可用通常的方法,如直接求f(x)的最值(分3种情况a≥5,a≤4,4 ( ) A.γ<α<βB.α<γ<β C.α<β<γD.β<γ<α (2017年浙江省数学高考试题第9题) 此题要求比较三棱锥D-PQR的3个面与底面所成二面角的平面角的大小,过点D作DO⊥平面ABC,垂足为O,则O为正△ABC的中心.分别设O到直线PR,PQ,QR的距离为d1,d2,d3,则 问题可转化为比较d1,d2,d3的大小. 图1 图2 如图2,由已知得点P,O,C共线,∠RQC=90°,∠ROC=90°,故点R,O,Q,C共圆,于是∠ORQ=30°,∠PRO>30°,因此d1>d3.同理可得d3>d2,从而 d1>d3>d2, tanα 即 α<γ<β. 故选B. 本题将空间问题平面化,这是解决立体几何问题的基本策略,如能画出比较准确的图形,利用直观也可得出结论(但要严格论证需要有较深厚的平面几何功底),考查了学生直观想象、推理论证等数学核心素养. 图3 1)求直线AP斜率的取值范围; 2)求|PA|·|PQ|的最大值. (2017年浙江省数学高考试题第21题) 本题是一道解析几何求变量的取值范围或最值问题,考查坐标化思想、数形结合思想、函数思想及转化思想,试题常规而不落俗套. 分析 1)直接利用经过两个点的直线斜率公式,得直线AP的斜率为 2)关键是|PQ|的计算.根据题目给出的信息,利用勾股定理计算|PQ|较简便. |PA|·|PQ|=(k+1)3(1-k). 此方法利用勾股定理,避免了求点Q的坐标带来的繁杂运算,也可利用向量法: 以上各种方法回避了韦达定理,借助图形的性质或向量,减少了运算量,因此也是规避题海的一个典例,考查了学生的数学建模、直观想象、数学运算等数学核心素养. 此外,试卷在数学知识的应用上也做足了文章,第20~22题都考查了导数的应用,凸显了导数应用的广泛性,考查了学生综合运用数学知识、思想和方法解决问题及数学建模等能力. 1.3 演绎经典,彰显鲜明特色 将以往的浙江省数学高考试题推陈出新,是浙江卷的一贯风格,2017年试卷尤其突出. 例5 已知数列{an}满足:x1=1,xn=xn+1+ln(xn+1+1)(其中n∈N*).证明:当n∈N*时, 1) 0 (2017年浙江省数学高考试题第22题) 本题给出的递推式中含自然对数,规避了题海,也是2017年试题的一个亮点,背景是泰勒展开式,考查导数的应用及放缩的策略.此题实际上是2006年浙江省数学高考理科压轴题改编而成的. 图4 例6 已知函数f(x)=x3+x2,数列{xn}(其中xn>0)的第一项x1=1,以后各项按如下方式确定:曲线y=f(x)在(xn+1,f(xn+1))处的切线与经过点(0,0)和(xn,f(xn))的直线平行(如图4),求证:当n∈N*时, (2006年浙江省数学高考理科试题第22题) 例5的第3)小题与例6的第2)小题证明的是同一个结论.例6直接从导数的几何意义出发设计问题,而例5隐去了导数的几何意义,需要考生去挖掘,对考生的数学能力来说是挑战.解决此题需综合运用数列、不等式、导数知识及分析、观察、归纳、猜想等能力及思维品质,入口宽,解法多样,能综合检测考生分析问题、解决问题的能力及进一步学习的潜能与潜质. 再如2017年数学高考卷的第7题由2007年理科卷第8题改编而来;第15题由2014年理科卷第8题改编而来;第17题由2008年理科卷第15题改编而来;第21题由2008年理科卷第20题改编而来.如此密集地演绎经典试题,并且都是重点题,创下了历年之最. 2017年试题秉承了浙江卷的特点,是文理合卷的一次有益探索,命题设计尽可能地从现实问题或几何背景出发,构造出素材朴实、内蕴丰富的试题,充分体现数学的内在实质.试卷中的题目处处闪现着问题解决的智慧,既加强了概念考查,又突出对学生能力的考查,对课堂教学是一种很好的引导,引导教师、学生避免将大量的精力消耗在盲目套用所谓的解题技巧上.这给我们昭示了一个信息:会思考、具有良好思维品质的考生能考出优异的成绩,也给我们的复习教学诸多启示. 学生缺乏的不是技巧,而是基础.在考试中,不少学生对概念、定理、公理等认识模糊,导致在遇到陌生问题时不知道如何运用所学知识去合理地展开联想,进行有效地探究,选择简便的方法.他们解答了大量的习题,但“大运动量的训练”不能使他们获得思考和解决问题的能力.研究每一章节的典型习题,注重“源”与“本”的关系,才能提高学生对“双基”的灵活运用. 高考试题源于课本与以往的高考试题,这是高考试题公平性的体现,以往的高考试题凝聚了命题教师的心血.可以通过专题的形式分条块进行,引导学生厘清每一条块是怎么考的,答题策略有哪些,蕴藏着哪些规律,问题的本质是什么. 数学重在思维,教学中教师需帮助学生纵横梳理知识和方法,实现知识条理化、有序化、网络化.对重点知识与重点方法,要理解准、透,对难点知识、方法适度开展探究式教学,从基本问题出发,从多角度探索、一题多变、策略提升、建立数学模型展开教学,帮助学生理解数学本质,提升学生的数学核心素养. �2017-06-11; 2017-07-03 郑日锋(1962-),男,浙江瑞安人,浙江省特级教师.研究方向:数学教育. O12 A 1003-6407(2017)08-41-04


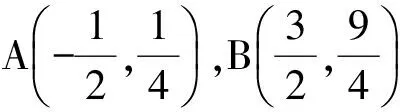


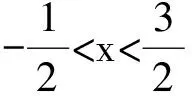


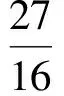


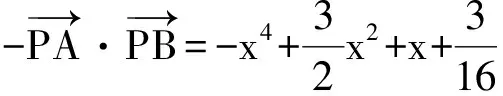





2 试题对教学的启示
——吴淼峰

