创设问题情境应注意的几个问题——以“解三角形”教学为例说明

☉江苏省扬中高级中学 陆昌荣

创设问题情境应注意的几个问题
——以“解三角形”教学为例说明

☉江苏省扬中高级中学 陆昌荣

问题教学法是目前教学中教师普遍采用的有效方法，但问题的设置要立足于教材、遵循学生的认知规律.笔者以解三角形教学为例，就问题情景的设置提出几点思考，供参考.

一、要立足于学生的最近发展区

问题情境创设，一定要紧扣课题，立足于学生的最近发展区，切记不要故弄玄虚，偏离主题，要有利于激发学生思维的积极性，要直接有利于当时所研究的课题的解决，既要考虑教学内容，又要考虑学生的差异，注意向学生提示设问的角度和方法.

师：我们知道一个三角形有三条边、三个角，如果给我们其中的某些边或角，让我们来求其他边和角或面积的过程，就是解三角形.

问题1：如果给我们一个直角三角形，我们如何来求其边或角？

生：利用勾股定理或三角函数相关知识求解.

问题2：如果是锐角或钝角三角形呢？

生：我们可以通过作辅助线，将其分割成直角三角形求解，如图1和图2.

图1

图2

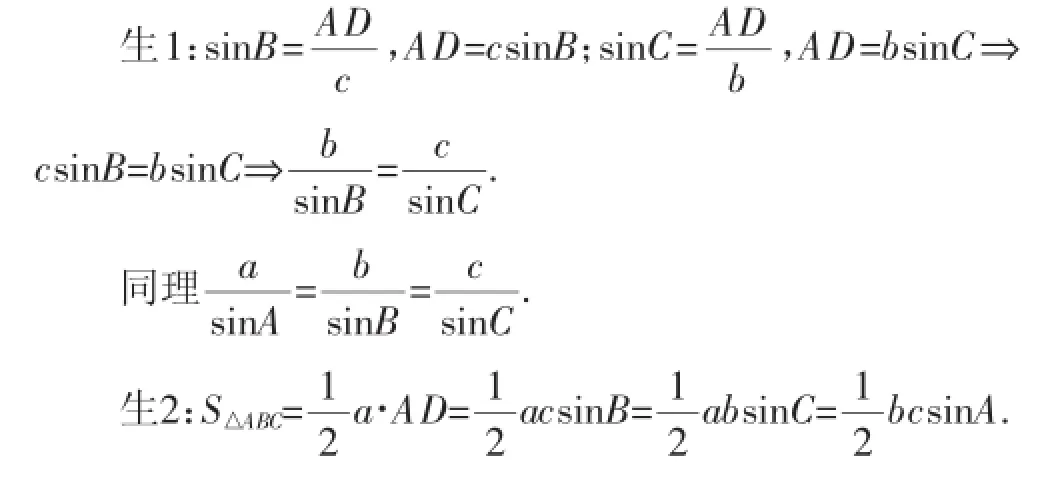
师：非常好！我们发现的这一规律，是一个非常重要的定理——正弦定理……

通过上述问题的引导，学生不仅得出了解三角形的重要工具：正弦定理，还得出了面积公式，可谓一举多得.

二、要启发引导，保持思维的持续性

教师的启发要遵循学生思维的规律，因势利导、步步释疑，切不可不顾学生的心理状态和思维状态，超前引路.

问题3：通过上面的探究，我们得出了正弦定理.那么什么条件下可以应用正弦定理？如何应用？

生1：给出两边及一边的对角或给出两角及一边.

生4：根据比例性质，还可以得出a∶b∶c=sinA∶sinB∶sinC.

……

问题4：正弦定理与三角形的边、角有关，那么以前我们学过哪些三角形的相关性质？如果利用这些性质？

生5：两边之和大于第三边，两边之差小于第三边.

生6：三角形的内角和等于π.

生7：三角形的一个外角等于与其不相邻的两个内角和.

问题5：在如图3所示的三角形中，你能发现哪些角的关系？

生8：A+B+C=π，∠ADC=B+∠BAD，∠ADB=C+∠CAD，∠ADB+∠ADC=π.

图3

例3在△ABC中，若2cosBsinA=sinC，则△ABC的形状一定是（）.

A.等腰直角三角形B.直角三角形

C.等腰三角形D.等边三角形

图4

又sin∠BDA=sin∠ADC，BD=CD，所以∠DAC=90°，所以∠BAC=120°.

在△ABC中，由余弦定理BC2=AB2+AC2-2AB·ACcos∠BAC，得BC2=48+12+24=84，BC=2

解法2：如图5，延长AD到点E，使AD=DE，连接BE，CE，易知四边形ABEC为平行四边形，所以BE= 2

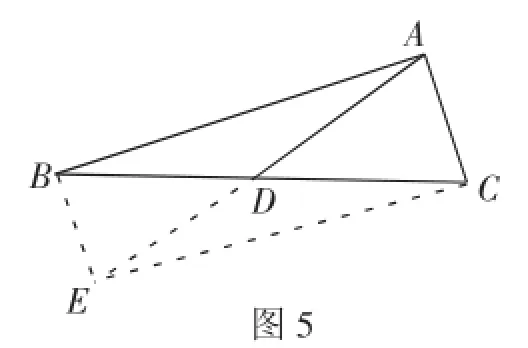
图5

在△ABC中，由余弦定理BC2=AB2+AC2-2AB·AC cos∠BAC，得BC2=48+12+24=84，BC=2

三、要注意问题的关联性

要不断向学生提出新的数学问题，要提出带有导向性、难度适宜、启发性的问题.其实，问题并不在多少，而在于是否具有启发性，是否是关键性的问题，是否能够触及问题的本质，并引导学生深入思考.

问题6：如果已知所给的是一个三角形的两边及它们的夹角，如果求其他的边和角？例如给出a，c和角B，如何求b.

生：还得利用分割法，将其分割为两直角三角形求解，如图6和图7.

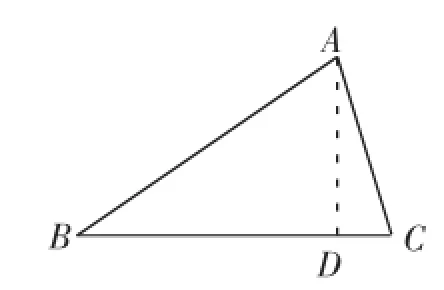
图6

图7

在Rt△ACD中，AD=csinB，CD=BC-BD=a-ccosB.

在△ACD中，由勾股定理得

b2=AD2+CD2=（csinB）2+（a-ccosB）2=c2sin2B+a2-2accosB+c2cos2B=a2+c2-2accosB.

问题7：如果给出的是a，b和角C，如何求c？

c2=a2+b2-2abcosC.

师：观察我们得出的这两个答案，有什么发现？

生：a2=b2+c2-2bccosA.

师：这就是解三角形的又一重要工具——余弦定理……

如果给出三边，如何求夹角？

图8

（1）求sin∠BAD；

（2）求BD，AC的长

通过上述问题展示的过程，我们不难发现，新知识的引入都是在问题的引导下自然生成，新知识的发现过程都是学生自主探究的结果.这样的探究不仅使学生掌握如何应用所学性质定理，也明了定理的来源.另外，在进一步的学习中，可引导学生根据所给的不同条件，如何选择应用两个定理解题，以及三条边、三个角，这6个量中是否给出其中的三个条件，就能求出其他的条件呢？给出两边和其中一边的对角，是否一定能构成三角形？如果能构成，三角形是否唯一？等等.