为教材做“注记”——以“点到直线的距离”为例

☉浙江省义乌市第二中学 龚辉斌

为教材做“注记”
——以“点到直线的距离”为例

☉浙江省义乌市第二中学 龚辉斌

数学教材凝结着教材编写专家的心血和智慧，受到教师们的普遍尊重，以教材为本是数学教学的基本遵循.然而，由于形式化表达的特点，数学中的一些深层次东西并不容易在教材中自然地表现出来.限于篇幅，一些重要的数学思想和方法也未能获得充分的显现.因此，立足教材理解，围绕数学教育目标，一线教师对教材内容进行自主的分析、加工和补充具有现实意义.有经验的数学教师习惯于把这些分析、加工和补充标注在教材的页眉或页脚位置（或其他空白处），以待有机整合在后续的备课活动中.我们不妨把教师的这种个性化活动称为“为教材做‘注记’”.为教材做“注记”有哪些基本的视角？各自有着怎样的教学意义？本文以高中数学课程标准实验教科书的一段内容为例，谈谈笔者的实践和思考，抛砖引玉，与同行交流.

一、案例

人教A版数学2（必修）第三章“直线与方程”3.3.3“点到直线的距离”开门见山，通过“思考？”栏目提出问题：如图1，已知点P0（x0，y0），直线l：Ax+By+C=0，如何求点P0到直线l的距离？

图1

教材给出了一种思路（下文简称“教材思路”）：首先，由PQ⊥l，以及直线l的斜率-，得l的垂线PQ的

00斜率为，从而求出垂线PQ的方程；接着，求出直线PQ

00与直线l的交点，即垂足Q点的坐标；最后，求出P0与Q间的距离|P0Q|，此即为点P0到直线l的距离.

教材指出，上述方法虽然思路十分自然，但具体运算较繁，因而采用下面的方法（下文简称“教材做法”）：

如图2，设A≠0，B≠0，则直线l与x轴与y轴都相交.过点P0分别作x轴和y轴的平行线，交直线l于R和S，得R的坐标为），S的坐标为于是有

图2

由三角形面积公式，得P0到直线l的距离

可以验证，当A=0，或B=0时，上述公式也成立.

对于上述教材内容，笔者给出了3点“注记”.

注记1，大致遵循“教材思路”，但不求垂足Q点的坐标，也能求出|P0Q|.

设垂足Q点的坐标是（x′，y′），则|P0Q|=

把x′-x0和y′-y0分别视为一个整体，建立关于它们的两个关系式.为此，需要转化已知条件.

因为Q在直线l上，所以Ax′+By′+C=0，变形为A（x′-x0）+B（y′-y）0+Ax0+By0+C=0（.1）

把（2）式代入（1）式，得

注记2：“教材做法”的核心是构造一个位置特殊的直角三角形，其数学考虑包括：

第一步，联想.从目标“点到直线的距离”出发，联想到“三角形边上的高”，进一步联想到“三角形的面积”.

第二步，设想.设想构造一个以P0为顶点的三角形，P0所对的边在直线l上，设这条边为SR（如图3）.

第三步，表示.P0到直线l的距离d=△P0SR中SR边上的高=

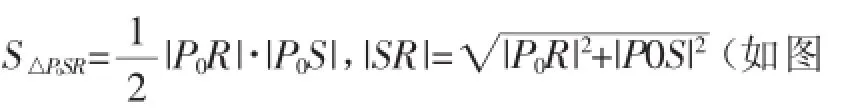
第五步，再特殊化.为使|P0R|和|P0S|的表示来得简易，让P0R∥x轴，P0S∥y轴（如图2）.

图3

图4

注记3：“教材做法”的关键词是“联想”和“特殊化”.事实上，还有其他的“联想”和“特殊化”.如联想以下事实：在△ABC中，BC边上的高hA=|AB|sin∠ABC，有以下方法（设直线l的倾斜角为α）：

过点P0作y轴的垂线交直线l于R，则点P0到直线l的距离d=|P0R|sinα.容易得到，|P0R|=，sinα=

二、思考

数学教材是一幅未竟的“画”，一段待续的“情”.事实上，把数学的学术形态转化为教育形态不是一件简单的事，需要教材编者和一线教师的配合与协作.体现教材实践者对于教材的能动性，使教材发挥最大的教学效益，是教师为教材做“注记”的出发点，必为教材编者所乐见.上文案例提供了为教材做“注记”的3个基本视角.

视角1，调整想法.这里的“想法”，指的是教材中处理具体数学问题的思路或意见.向教材学习是教师应有的态度，但教材不是“圣经”.借助于研究性阅读，教师会发现教材的一些想法其实有着调整的空间.对此，汲取其合理成分，教师以“注记”的形式写下调整的结果，不仅丰富了课堂教学资源，同时孕育了新的教学价值.

点P到直线l的距离，本质上是“点与点之间的距离”，即点P与直线l上的一个特殊点之间的距离.分析这个特殊点（垂足Q）的几何性质（在直线l上，与点P的连线垂直于直线l），然后转化为代数关系（坐标满足直线l的方程，与点P的连线的斜率等于直线l的斜率的负倒数），体现了“聚焦核心对象→分析几何性质→进行形数转化”这一解析几何的基本思想和研究套路，教学意义不言而喻.从问题目标出发，通过“设而不求”、“整体代入”等数学技能的运用，注记1有效调整了教材想法（实际上改进了教材思路）.将之运用于课堂教学，等于给予学生一次践行解析几何思想、提高分析问题能力、发展重要数学技能的良机.

注记1可以避免教学“入宝山而空返”的尴尬，同时有利于培养学生的理性精神.在学生的心目中，数学教材是“高大上”的学习材料，因而课堂上教师抛出问题“不求垂足Q点的坐标也能求出吗？”时，学生的内心会充满疑惑.以注记1指导学生的尝试，让他们亲历峰回路转的时刻，看战术的改变如何使教材思路唤发了新的生机.学生将感受到：独立自主的思考和积极的行动尝试，是多么的可贵！从而增强学生自我发展的信心.

视角2，诠释做法.教材展现给人的是逻辑严密的问题解决流程，背后的思维活动往往被“雪藏”了“.注记”的一个重要方面是化“隐”为“显”，从帮助学生理解数学思维的角度重拾生动活泼的思考过程.

构造法是数学的重要方法，但在中学数学教材中并不多见，学生感觉其“妙”易，理解其“意”难.事实上，一个代数式或空间图形的构造，往往不是随性而起、一拍脑袋而成的，而是一连串数学考虑的结果“.教材做法”构造了一个三角形，背后的思维活动是“联想”和“特殊化”.即由“点到直线的距离”联想到“三角形边上的高”；围绕“如何求出三角形的高”，采取了两次特殊化行动.具体地说，点到直线的距离三角形边上的高直角三角形斜边上的高两条直角边分别垂直于x轴和y轴的直角三角形斜边上的高.联想是数学创造的源泉，特殊化则反映了数学科学的特点，即“追求简单（包括简单的过程和简单的结果）”．“注记2”诠释了图2的来龙去脉，可以使学生真切体会联想和特殊化在数学构造中的意义和作用，“构造”这一抽象的数学思想由此变得生动起来．

视角3，补遗方法．数学思想是一种策略性知识，是数学的精髓．策略性知识的学习，学习者的亲身实践和具体方法的支撑不可或缺．因此，对于教材反映的重要数学思想，教师有必有趁热打铁，给予学生强化体验的机会．一条自然、经济的途径是引导学生从教材做法反映的数学思想出发，尝试重新解决教材提出的问题，让学生借助改进或创新的数学方法来推进自己对数学思想的理解．教师以“注记”的形式写下有关数学方法的补遗，正是为了有效地指导学生的这种实践活动．

“注记2”可以使学生感受“联想”和“特殊化”在数学构造中的作用，可它毕竟属于接受性学习．引导学生展开新的联想，鼓励学生尝试新的特殊化，可以促成学生运用联想思维和特殊化方法进行数学构造的直接经验．“注记3”为学生的这一活动提供了强力支持，避免数学思想（构造思想）教学浅尝辄止的现象．

总的来说，抓住数学知识发生发展的契机，聚焦数学思想的阐释和应用、数学方法的改进和创新，3个视角开启了深化教材理解、发展教材资源的窗口．当然，从数学内容和教材编写的实际出发，上述视角应有所侧重，并采取一定的审慎态度．如，教材想法确有调整的必要吗？如何使教材做法的诠释更到位？补遗的数学方法符合学生的知识经验和认知水平，并能促进学生的思维发展吗？在笔者看来，同一备课组老师经常就“注记”的具体内容展开讨论，是保证“注记”准确、深刻、全面的必要举措．

1.人民教育出版社·课程教材研究所·中学数学课程教材研究开发中心．普通高中课程标准实验教科书·数学必修2（A版）［M］.北京：人民教育出版社，2010．

2.王丽娟，殷玉波．复盘“点到直线的距离”说课［J］．中学数学（上），2014（7）．