从高考试题研究教学导向

☉江苏省苏州第四中学 薛荣明

从高考试题研究教学导向

☉江苏省苏州第四中学 薛荣明

众所周知，高考试题是经过许多专家、特级教师多次研究、反复推敲命制的结果，每一个原创考题的背后都有着大量的思考，汇聚了多个知识考查的整合.但是从现阶段复习教学与高考导向来看，我们很多时候的数学复习工作都是无用功，即不少教师并不研读考试大纲、不钻研高考真题、不了解命题意图、不思考真题的高等数学背景等等一系列问题，导致复习教学的效果多数时间是无用功.

某位命题专家说得好：研究高考真题可以获得很多信息，比做一本无用的资料实在得多，可以反复做、变式做，会有很多体会的.笔者就近年选出部分真题与读者一起分享，教学应该有如何的导向，不当之处恳请批评指正.

一、概念怎么考

数学概念在每份高考卷中都有体现，但是怎么考才能体现数学味？怎么考才能有区分？近年来概念考查愈来愈趋向知识的本质、注重概念的理解.以函数为例，函数考什么？函数是高中数学学习的基础，对它的考查应该考最能体现函数本质的核心知识和思想方法.对于考查的形式应该是不拘一格的，应该有利于促进学生核心素养的形成、发展与应用，摆脱模式化的解题教学，同时也是能适度促进函数与平面向量、三角、不等式等其他模块知识的融合与交汇，以区分学生对于概念的理解，增强选拔区分功能.

问题1存在函数f（x）满足，对任意x∈R都有___________.

（1）（fsin2x）=sinx；（2）（fsin2x）=x2+x；（3）（fx2+1）=|x+ 1|；（4）（fx2+2x）=|x+1|.

函数概念视角分析：何为函数？自变量当取x0对应唯一的y0.深刻理解函数概念，才能对问题的解决有更深刻的理解.比如对（1）来说，不妨令x=0，得（f0）=0，再令x=，得（f0）=1，显然对于同一个自变量而言，（f0）不唯一，这与函数定义相违背，因此（1）不满足题意，其余类似.故（4）正确.这是从深度理解函数概念的视角进行了考查、辨析.

周期性质视角分析：f（sin2x）的内函数的周期是π，而sinx的周期是2π，（1）不符；f（sin2x）的内函数的周期是π，x2+x不具有周期性，（2）不符；f（x2+1）内函数是偶函数，而|x+1|不具有奇偶性，（3）不符.故选（4）.

评析：此题考查了函数的概念与基本性质，要求学生对概念与性质有一个深刻的认识才能快速高效地作出判断.此题最关键的难点是题干叙述得非常数学化——数学符号语言——学生抓不住问题的核心.从本题看来，高考对于概念本质的考查愈来愈深入，对学生形式化理解的考查愈来愈追求核心，从而达到区分的目的.因此概念教学不能只停留简单问题的表面，要深入了解概念内涵、本质，并运用于试题中.

问题2设函数f（x）=sin2x+bsinx+c，则f（x）的最小正周期与b______（填写有关或无关），与c______（填写有关或无关）.

分析：学生对于周期的理解主要是限于函数f（x）= Asin（ωx+φ）（A＞0，ω＞0），而且基本属于背诵公式求周期，对周期的概念并没有真正的理解.其实我们可以这样思考，f（x）=sinx周期是2π，f（x）=sin2x周期是π，它们结合在一起，则函数f（x）=sinx+sin2x的周期必定受到影响，因此对于本题我们就理解哪个系数对于周期有影响了.由于（fx）=sin2x+bsinx+c=+bsinx+c.当b=0时，（fx）的最小正周期为π；当b≠0时，（fx）的最小正周期为2π.c的变化会引起（fx）图像的上下平移，不会影响其最小正周期.

评析：本题主要考查三角恒等变换、三角函数的最小正周期等基础知识，意在考查学生的分析问题和解决问题的能力.周期概念的理解，成为周期考查的新导向，不再拘泥于仅仅记忆周期相关的公式，从而提高了学生对周期概念的理解和认识.

二、背景怎么挖

数学是什么？数学是一种语言.我们日常的教学就是不断地在将文字语言、图形语言与数学符号语言之间化归转化.将我们不熟悉的语言环境通过我们自身的数学基础，结合题目本身的要求转化为熟悉的一个一个环节将问题串联起来，挖掘试题的物理背景、几何背景，将问题还原再解决.

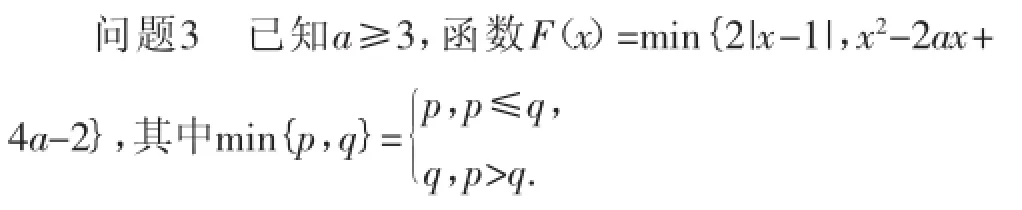
（1）求使得等式F（x）=x2-2ax+4a-2成立的x的取值范围.

（2）①求F（x）的最小值m（a）；

②求F（x）在区间［0，6］上的最大值M（a）.

“max”与“min”是高等数学中的基本表述符号，对于高等数学而言，命题专家如何让其在中学数学中体现落地？这很好地体现了高考命题的特点：题干简洁明了，特别注重数学符号语言的应用.本题考查的主体是二次函数，涉及函数的基本考查点：单调性、最值.

简析：（1）由于a≥3，所以，

当x≤1时，（x2-2ax+4a-2）-2|x-1|=x2+2（a-1）（2-x）＞0；

当x＞1时，（x2-2ax+4a-2）-2|x-1|=（x-2）（x-2a）.

所以，使得等式F（x）=x2-2ax+4a-2成立的x的取值范围为［2，2a］.

第（1）问给我们搭建的平台切入点还是很适合的，主题解决三个层面的问题：遇到绝对值问题应该怎样处理？分类讨论后是二次问题，我们处理的通性通法是什么？处理好定性分析与定量计算的关系以及先后顺序.大量的问题出现在对于当x≤1时，处理的手段是有限与呆板的——解不等式，缺乏先定性分析，再定量计算的策略储备，要充分利用好已知条件：a≥3与隐含条件：函数过定点（2，2）.

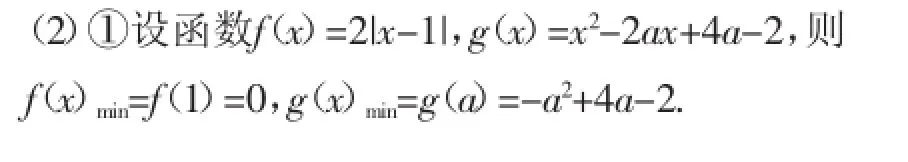
所以，由F（x）的定义知，m（a）=min｛f（1），g（a）｝，

②当0≤x≤2时，F（x）≤f（x）≤max｛f（0），f（2）｝=2= F（2），

当2≤x≤6时，F（x）≤g（x）≤max｛g（2），g（6）｝= max｛2，34-8a｝=max｛F（2），F（6）｝.

第（2）问在函数图像上，运用单调性分析的方法找到产生最大值与最小值的点，最后比较大小找到字母的分界点.最后还要认识到M（a）是含有字母a的表达式，而不是再用一次求最值的策略剩下常数.明确字母a是给定范围内的任意一个常数，就已经是常数了，不需要再求最值.

评析：重视思想，意蕴深刻.本题涉及到了数学中最常用的“函数与方程、数形结合、转化与化归、分类讨论”的数学思想方法，其意蕴丰富而又深刻.高中数学教学要回归教材，养成挖掘教材试题的本质与背景的习惯，要重视思维的启迪，重视问题的研究，克服“满堂灌、重训练”的现象，在培养学生的思维能力.

三、创新怎么办

高考问题之所以难，还有一个重要因素是高考问题的原创性.学生在复习教学中往往训练的模拟问题是延续一定的套路性，但是高考为保障公正公平恰恰将这种套路性的问题一一去除，以更为公平的背景设计考题，因此高考导向暗示复习教学需要一定的独特性，不能总是一层不变的按照老套路复习.

（1）f（x）≥1-x+x2；

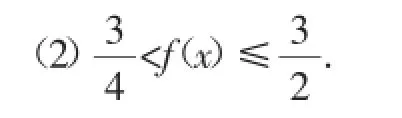
分析：在大量研究二次函数、绝对值函数、三次函数求导的今天函数教学中，某省以这样的压轴函数试题设计，远远超出教师与学生的预想的，是一种大胆的创新，问题设置向思维靠拢——以证明题的形式面世.但问题的落脚点还是基于通性通法——比较大小要回归作差法或者构造，出现（1+x）（fx）≥1-x+x2，g（x）=（1-x+x2-x3），或g（′x）=-（-1+2x-3x2），g（′x）=入口比较容易，对学生的思维能力和解题能力提出了非常的要求.证明题的要关注小问之间的关联性；出现（fx）≥1-x+x2或1-x+x2=不等式的证明着眼于放缩：令（fx）=g（x）+1-x+x2，（fx）max≤g（x）max+（1-x+x）2max，（fx）min≥g（x）min+（1-x+x）2min，g（x）∈或（1-x+x）2

四、教学怎么办

“高考考什么，怎么考”永远是高中教学的风向标，命题风格，数学的本质以及高考中学生答题出现的问题是教师改进教学的重要依据.从高考命题的方向来看，一味大训练量的复习教学已经不适合当下的数学复习教学了.不少教师往往对高考导向没有深入的思考，从而将复习教学变得既无效又耗时.

其一，加强概念教学的深刻性.从上述函数概念、周期概念的考查来看，在不少中学数学重要概念的复习中还有进行有效挖掘，比如圆锥曲线的概念、平面向量基本定理的概念等，近年来也有不少高考亮题出现，教师复习教学要多多关注.

其二，复习教学要紧紧靠拢高等数学.很多高考真题都是大学专家命制的，必然具备了一定的高等数学背景，教师教学要多思考这些背景，更要多看看相关专业杂志，获取更多的知识背景.

最后是关注思想方法的渗透，比如原创性问题必定依靠常见的数学思想而编制，有了思想问题的解决几乎是必然的，这是教学的主要导向.以问题4为例，其第一小问只需要利用作差即能解决，这是多项式比较的最基本解题思路.

后续教学要多思考这些环节，在模拟套路试题的训练上适可而止，这样的教学才是有效的、有指导意义的.

1.柴贤亭.数学教学中的思维启发设计［J］.教学与管理，2014（10）.

2.郑毓信.解题教学理论的必要发展［J］.中学数学月刊，2014（1）.