例谈分类讨论在解题中的运用

☉内蒙古赤峰市赤峰二中 孙广仁

例谈分类讨论在解题中的运用

☉内蒙古赤峰市赤峰二中 孙广仁

分类讨论的思想方法是中学数学的基本思想方法之一，是历年高考的重点.函数试题中含有需讨论的参数，是历年高考的热点.然而在分类讨论时，讨论的标准是什么？怎样进行分类讨论？如何在分类时，做到不重不漏？很多学生知道利用分类讨论，但是不知道该如何进行，往往很混乱.基于这些问题，本文以近几年的高考题为例，谈谈分类讨论在解题中的运用.

一、利用数形结合进行分类讨论

正确、合理运用数形结合是学好高中数学的关键，因此要培养学生数形结合的能力，并会根据数形结合进行分类讨论.

例1关于x的方程（x2-1）2-|x2-1|+k=0，给出下列四个命题：

①存在实数k，使得方程恰有2个不同的实根；

②存在实数k，使得方程恰有4个不同的实根；

③存在实数k，使得方程恰有5个不同的实根；

④存在实数k，使得方程恰有8个不同的实根.

其中假命题的个数是（）.

A.0B.1C.2D.3

解：据题意可令|x2-1|=t（t≥0），①则方程化为t2-t+k=0.②作出函数y=|x2-1|的图像，如图1，结合函数的图像可知，

图1

（1）当t=0或t＞1时，方程①有2个不等的根；

（2）当0＜t＜1时，方程①有4个根；

（3）当t=1时，方程①有3个根.

所以，当t=0时，代入方程②，解得k=0，此时方程②有两个不等根t=0或t=1，故此时原方程有5个根.

作出函数的图像，要使函数与y=kx-2有两个不同的交点，则直线y=kx-2必须在阴影部分内，如图2，此时当直线经过右上区域时B（1，2），k满足1＜k＜4；当经过左下区域时，k满足0＜k＜1.

综上实数k的取值范围是（0，1）∪（1，4）.

图2

二、利用数轴标根进行分类讨论

数轴标根形象直观，利用数轴标根来进行分类讨论简单明了，易于理解.

例3已知函数f（x）=（x-2）ex+a（x-1）2，讨论f（x）单调性.

解：因为f′（x）=（x-1）（ex+2a），且对任意x∈R，ex＞0.

所以，（1）当a≥0时，若x∈（-∞，1）时，f′（x）＜0；

若x∈（1，+∞）时，f′（x）＞0.

（2）当a＜0时，令f′（x）=0，则x=1或x=ln（-2a）.

所以，当x∈（-∞，1）或x∈（ln（-2a），+∞）时，f′（x）＞0；当x∈（1，ln（-2a））时，f（′x）＜0.

所以，当x∈（-∞，ln（-2a））或x∈（1，+∞）时，f′（x）＞0；当x∈（ln（-2a），1）时，f（′x）＜0.

所以，当x∈（-∞，+∞）时，f（′x）≥0.

本题难点在于a＜0的情况，此时f′（x）=0有两个根，1和ln（-2a）.需要分类讨论，由数轴标根法可知，根的大小是关键，为此，根据两根的大小不确定为标准，这就是a以-为临界进行分类讨论的原因.

图3

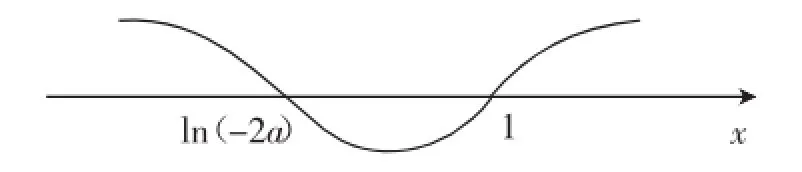
图4

图5

从以上分析可知，数轴标根法刚好为我们提供了分类讨论的标准，同时也为我们打开了解题思路.根据这种方法来分类讨论，可以做到不重不漏.另外，在运用数轴标根法解不等式时要注意：不等式的首项系数要是正数；“奇穿过，偶弹回”的原则.

三、利用用构造函数进行分类讨论

例4在平面直角坐标系中，横坐标和纵坐标都是整数的点称为格点，任取6个格点Pi（xi，yi）（i= 1，2，3，4，5，6）满足：（1）|xi|≤2，|yi|≤2，（i=1，2，3，4，5，6），（2）任何三点不在同一条直线上.试证：在以Pi（i= 1，2，3，4，5，6）为顶点的所有三角形中，必有一个三角形，它的面积不大于2.

证明：用反证法，假设在以Pi（i=1，2，3，4，5，6）为顶点的所有三角形面积都大于2.

可知若某相邻两条平行线上有三个点，则它们构成的三角形的面积不大于2.

（1）x轴上无点或恰有一点，则至少有三个点在x轴上方（或下方），则这三点构成的三角形的面积不大于2，矛盾.

图6

（2）x轴上二点，若y=±1上有点，出现矛盾，则只能是y=±2上各有两点.

（3）同样讨论y轴，知y轴上有两点，则x=±1上无点.

则只能如图6中9点中放6点.

若取到原点，则x轴上（-2，0）和（2，0）中任取一点，在y=±2上任一点构成三角形，即得矛盾.

若不取原点，则必取x轴上（±2，0），y轴上（0，±2），则在余下的四点（±2，±2）中任取一点均可得矛盾.

从而命题得证.

四、利用描述分析进行分类讨论

（2）当a=1时，（fx）=1∈［-2，2］.

（3）当a＞1时，1-a＜0，

例6已知a是实数，函数f（x）=2ax2+2x-3-a，如果函数y=f（x）在区间［-1，1］上有零点，求a的取值范围.

解：若a=0，则f（x）=2x-3，当f（x）=2x-3=0时，解得x= 1.5∉［-1，1］，所以a≠0.

当a≠0时，若Δ=0，即抛物线与x轴有唯一的一个公共点，此时：

当抛物线与x轴在［-1，1］上有唯一的一个公共点，此时a满足下列条件：

f（-1）·f（1）≤0，即（a-1）（a-5）≤0，解得1≤a≤5.

当a=5时，Δ=22-8×5×（-3-5）=324＞0，抛物线与x轴有两个不同的交点，所以，1≤a＜5符合要求.

当抛物线与x轴在［-1，1］上有2个公共点，此时a满足下列条件：

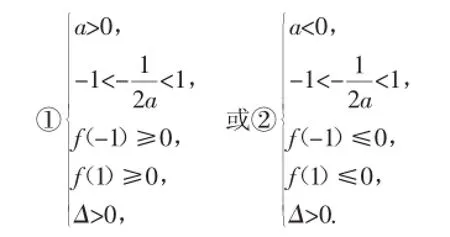
例7设函数fn（x）=xn+bx+c（n∈N+，b，c∈R）.

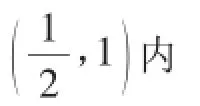
（2）设n=2，若对任意x1，x2∈［-1，1］，有|f2（x1）-f2（x2）|≤ 4，求b的取值范围；

解：（1）证明：b=1，c=-1，n≥2时，fn（x）=xn+x-1.

（2）当n=2时，f2（x）=x2+bx+c.

对任意x1，x2∈［-1，1］都有|f2（x1）-f2（x2）|≤4等价于f2（x）在［-1，1］上最大值与最小值之差M≤4，据此分类讨论如下：

综上所述，b的取值范围为-2≤b≤2.

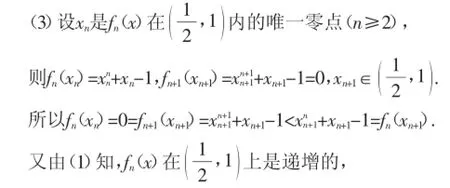
所以xn＜xn+1（n≥2），

所以数列x2，x3，…，xn…是递增数列.

由此可见，分类讨论是培养学生思维方式的极好素材，用分类讨论思想来解题，关键是要把握好三关：一是分类的对象要确定，标准要统一，做到不遗漏、不重复，分清主次，不越级讨论，即把好“分类关”；二是要保证条理分明，层次清晰，把好“逻辑关”；三是要对照题中的限制条件或隐含信息，合理取舍，把好“检验关”.