一类无理不等式的简证、推广与猜想

☉四川省成都市彭州中学 刘大华 黄秦安

一类无理不等式的简证、推广与猜想

☉四川省成都市彭州中学 刘大华 黄秦安

一、问题

文［2］又给出了一道多重根式不等式征解问题：

两道多重根式型不等式属于同一类无理不等式，它们在形式上十分优美，在本质上问题1显然是问题2的加强，即证明了问题1，问题2也就随之得证.然而无理不等式证明渠道多，技巧性强，如换元法、待定系数法、柯西不等式法、放缩发等.对于此类无理不等式，原文给出的证法是先构造两个数列，再根据数列的增减性放缩证明，过程十分繁杂，且构造和放缩本身都具有很大的思维推进障碍.

二、简证

分析：将根号去掉，化无理式为有理式是该题证明的核心，要实现此目标需经两次放缩过程，第一次运用简单不等式“n≤4n-1，n∈Z+”予以放缩，第二次看似“无中生有”地加“1”，实则将无理式“4n-2+”配成了完全平方式“

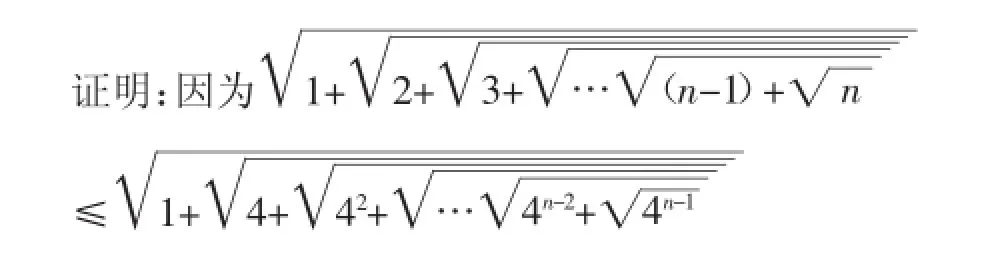
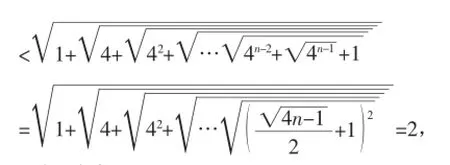
即问题1得证.

评注：上述简证干净、利落，当最里层的被开放部分放缩成完全平方式后，产生层层开方的连锁效应，不等式便获证.

三、推广

罗增儒教授说过：“问题一旦获解，就立刻产生感情上的满足，从而导致心理封闭，忽视解题后的再思考，恰好错过了提高的机会，无异于‘入宝山而空返’.”受此教导，笔者在将问题解决后习惯性地尝试多角度展开思绪，以求扩大战果.

思考1：在问题1、2中，层层被开方数“1，2，3，…，n”显然是公差为“1”的很简单等差数列形式，能否弱化条件，将其推广为公差为任意实数“a”的等差数列“ka，（k+ 1）a，（k+2）a，…”的形式？

证明：当n=k时，上式显然成立.

综上所述，推广1对一切k（1≤k≤n）都成立.

思考2：推广1将公差为“1”的简单等差数列扩充为公差为“a”的等差数列“ka，（k+1）a，（k+2）a，…”形式，若在层层根号前引入参数“m”，能否将其推广为更一般的任意等差数列｛an｝呢？

推广2已知n是大于等于2的整数，数列｛an｝是公差d≥0的正项等差数列，m＞0，则

分析：由于上述不等式与推广1不等式形式类似，故继续运用反向数学归纳法予以证明.然成立.

综上所述，推广2得证.

思考3：推广1、2都是处于洞悉了层层被开方数“1，2，3，…，n”是公差为“1”的简单等差数列后的思绪延续，若层层被开方数“1，2，3，…，n”不变，而改变其开方次数，还能够得到优美的推广结论吗？

要证推广3，需借助文［3］中关于一个加权幂平均单调性的引理.

下面结合引理对推广3实施证明.

综上所述，推广3得证.

美国著名数学家P.R.Halmos说：“问题是数学的心脏.”是的！有价值的数学问题往往是数学思维得以发展的桥梁.本文所涉及的无理不等式问题在其形式与内涵上具有双重美，其魅力在不断思考与火热探究的过程中光彩绽放.

四、猜想

最后，笔者提出一些待解决的类似无理不等式猜想，请读者否定或证明.

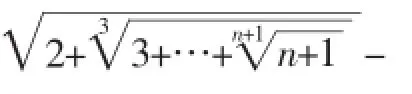
1.尚生陈.数学问题与解答2250［J］.数学通报，2015（6）.

2.宋庆.数学问题与解答2162［J］.数学通报，2014（1）.

3.匡继昌.常用不等式（第四版）［M］.济南：山东科学技术出版社，2010.

4.刘再平.从一道多重根式不等式趣题谈起［J］.中学数学研究（上半月），2015（1）.

5.马乾凯，李明.一个根式不等式的推广［J］.中学数学教学参考（上旬刊），2011（4）.

6.安振平.一道IMO预选题加强的再探究［J］.中学数学（上），2015（10）.