一道课本例题的研究与拓展

☉江苏省常熟市尚湖高级中学 马晋华

一道课本例题的研究与拓展

☉江苏省常熟市尚湖高级中学 马晋华

前苏联数学家奥加涅相说过：“很多例习题潜在着进一步扩展其数学功能、发展功能和教育功能的可行性.”教材中的习题凝聚了许多专家、学者的心血和经验.在教学过程中，应该充分利用教材上的经典例习题，采用多层次处理、多角度分析、深挖隐藏于习题背后的丰富内容，发挥其潜在的教学价值，无论从方法上还是内容上都起着“固体拓新”之用，可收到“秀枝一株，嫁接成林”之效，同时可培养学生提出问题和解决问题的能力，并使学生探究能力和创新能力得到发展.下面就一道课本习题谈其教学价值，整理成文，不揣冒昧，奉献出来，供读者参考.

一、题目再现

题目：如图1，过抛物线焦点F的直线交抛物线于A，B两点，通过点A和抛物线顶点的直线交抛物线的准线于点D，求证：直线DB平行于抛物线的对称轴.

在以往的教学中笔者都是直接讲解此例，但是发现绝大多数学生难以掌握，不知其所以然.我对此进行了反思，并改变了教学方式，先将此例具体化为特殊的抛物线y2=4x进行研究，然后推向一般即得例题结论，再进一步进行变式探究收到了良好的效果.

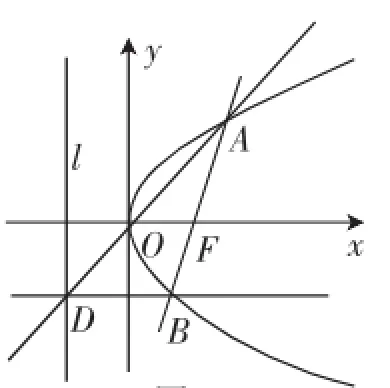
图1

二、改编、变式与拓展

改编例题：过抛物线y2=4x焦点F的直线交抛物线于A（x1，y1），B（x2，y2）两点，通过点A和抛物线顶点的直线交抛物线的准线于点D，求证：直线BD∥x轴.

在证明此例之前，先给出引例：

过抛物线y2=2px焦点F的直线交抛物线于A（x1，y）1，B（x2，y2）两点，求证：y1y2=-p2.下面先给出引例的证明.

证明：显然直线AB斜率不为0，故令AB方程为x= my+，代入y2=2px并整理得y2-2pmy-p2=0.

因为Δ=4p2m2+4p2＞0，所以y1y2=-p2.

再给出汉编例题的证明.

证明：如图1，因为A，O，D三点共线，

所以kOA=kOD（直线OA与OD斜率相等）.

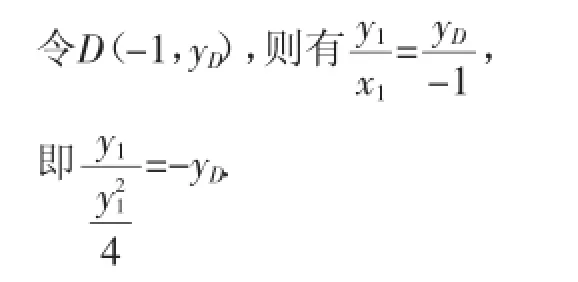
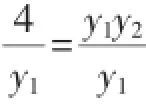
再让学生把结论推向一般式y2=2px，学生很快解决了问题.我紧接着对例题进行变式，并让学生证明，然后把结论推向一般.

变式1过抛物线y2=4x焦点F的直线交抛物线于A（x1，y1），B（x2，y2）两点，过B点作x轴平行线交准线于点D.求证：A，O，D三点共线.

所以kOA=kOD.所以A，O，D三点共线.

变式2过抛物线y2=4x焦点F的直线交抛物线于A（x1，y1），B（x2，y2）两点，过B点作x轴平行线与AO延长线交于一点D.求证：D点在一条定直线上.

证明：如图1，令D（xD，y2）.

因为A，O，D三点共线，所以kOA=kOD，

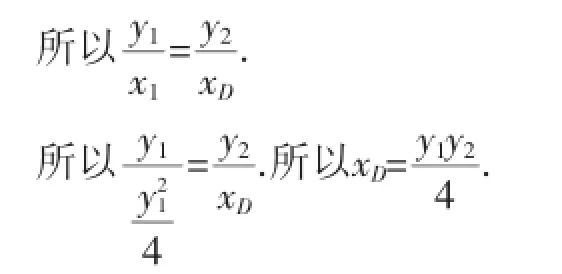
又由引例知，y1y2=-4.

所以xD=-1，即D点在定直线x=-1上.

拓展1过点M（2，0）的直线交抛物线y2=4x于A（x1，y1），B（x2，y2）两点，过点B作x轴平行线与AO延长线交于点D.求证：D点在一条定直线上.

图2

证明：如图2，显然直线AB斜率不为0，故令AB方程为x=my+ 2，A（x1，y1），B（x2，y2），D（xD，y2）.

代入y2=4x并整理得y2-4my-8=0.

因为Δ=16m2+32＞0，

所以y1y2=-8.

因为A，O，D三点共线，所以kOA=kOD，

所以xD=-2，即D点在一条定直线x=-2上.

拓展2过点M（a，0）（a＞0）的直线交抛物线y2=4x于A（x1，y1），B（x2，y2）两点，过点B作x轴平行线与AO延长线交于点D.求证：D点在一条定直线上.

同理可证定直线为x=-a.

变式3如图1，已知D为抛物线y2=4x准线上一点，抛物线焦点为F，过D作x轴平行线与抛物线交于一点B（x2，y2），直线BF与DO延长线交于一点A（x1，y1），求证：点A在抛物线上.

证明：令A（x1，y1），D（-1，y2）.

当直线AB斜率存在时，

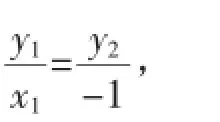
故点A在抛物线上.

所以点A在抛物线上.

变式4如图1，已知D为抛物线度y2=4x准线上一点，抛物线焦点为F，连接DO并延长与抛物线交于一点A（x1，y）1，过点D作x轴平行线与直线AF交于一点B（x2，y2）.求证：点B在抛物线上（.证明略）

变式5如图1，已知D为抛物线y2=4x准线上一点，抛物线焦点为F，连接DO并延长与抛物线交于一点A（x1，y）1，过点D作x轴平行线与抛物线交于一点B（x2， y2）.求证：A，F，B三点共线.（证明略）

三、几点思考

1.学生的主观能动性得到发挥

让学生自己去研究问题，获得对知识的再发现，这本身就是获取知识的心路历程，要让学生知晓探究知识的过程是艰辛的，但是获取知识的结果是一件令人兴奋的事，同时也体现了对学生的教不一定非要在课堂讲授，也可以是课外，教学和研究是相辅相成的，双方是充满互动的.教师在教学中可以在这方面多研究，多下工夫，这对学生的成长历程都是有帮助的.正如日本数学教育家米山国藏所说：“学生在学校所学的数学知识，毕业后若没什么机会去用，一两年后就会忘掉.然而，不管他从事什么工作，唯有深深铭刻在心中的数学的精神，数学的思维方法、研究方法、推理方法和看问题的着眼点等，却随时随地发生作用，使他们受益终生.”通过这次研究性学习，使我深深意识到除了做好日常教学外，可以多开展这样的研究性学习，使学生学中乐、乐中学，真正做到教学相长.

2.利于学生解题经验的总结与反思

纵观几十年的高考试题，许多高考试题也来源于课本教材.教材中的例题习题具有典型性、示范性，同时也渗透着一些数学思想方法或提供某些结论.因此，以本为本，重视对教材中的例题习题的深入探究，发现新的东西，是提高高考复习效率的最佳捷径.

3.引导学生重视回归课本

挖掘课本习题的教学价值，可引起师生对高三复习回归课本的重视，更有利于将学生从“题海”中“拯救”出来，对于激发学生的学习兴趣，养成用新视角审视课本习题的习惯，提升学生的数学素养大有裨益.教师在高三的教学过程中不要舍本逐末，拿着一本资料教到底，而应就地取材，注重应用新课程理念，对教材经典的例题和习题进行“再创造”，推陈出新，有效地帮助学生提高复习效率.人们常说“一种习惯会孕育一种思维方式”，如果教师能长期在引导、启发学生思考和提出问题上形成一种习惯和模式，学生就会养成遇事自己开动脑筋，自己寻找解决问题的途径和方法，不依赖他人的好习惯，那么课堂就会成为研究问题的课堂.数学家克莱因曾说过：“数学是人类最高超的智力成就，也是人类心灵最独特的创作，音乐能激发或抚慰情怀，绘画使人赏心悦目，诗歌能动人心弦，哲学使人获得智慧，科学可改善物质生活，但数学能给予以上一切.”

正如美国著名数学教育家波利亚所说：“一个专心的认真备课的老师能够拿出一个有意义的但又不太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就像通过一道门户，把学生引入一个完整的理论领域”.教师要研究教学，将课本上数学知识的学术形态转化为教育形态，让“冰冷的美丽”引起学生“火热的思考”.