对一道课本例题的变式教学
☉合肥师范学院数学与统计学院 邓珍珍☉合肥师范学院数学与统计学院 张新全
对一道课本例题的变式教学
☉合肥师范学院数学与统计学院 邓珍珍
☉合肥师范学院数学与统计学院 张新全
扎根于课本的数学变式教学是通过不同角度、不同侧面、不同情形、不同背景的变化,使学生有效地加深对数学知识的认识和理解,有意识地引导学生从“变”的现象中发现“不变”的本质,再从“不变”中探求规律.数学变式教学不仅很好地解释了“中国学习者悖论”,而且其一题多变、一题多解、多题归一(一法多用)和一题多用的变式给学生以新鲜感,增加了学习兴趣,减轻了学习负担,提高了教学有效性,培养了学生良好的思维品质.下面是我们对一道课本例题进行的变式教学设计.
题目:(沪科版八年级上册数学等腰三角形课后例题)已知:如图1,在△ABC中,AB=AC,∠BAC=120°,D、E是底边上两点,BD=AD,CE=AE.求∠DAE的度数.
思路:通过分析条件,很容易想到从三角形内角和为180°与等腰三角形底角相等出发,尽可能多地求出图中角的度数,最终求出所求角的度数.
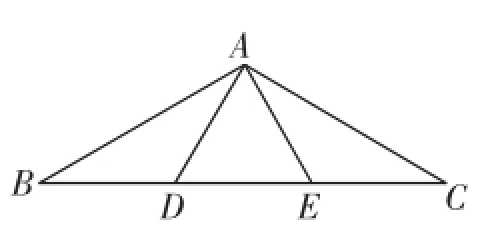
图1
因为BD=AD,所以∠BAD=∠B=30°.
同理可得:∠CAE=∠C=30°.
所以∠DAE=∠BAC-∠BAD-∠CAE=120°-30°-30° =60°.
一、改变条件,抓住本质
变式1:本例去掉条件AB=AC,能否求得∠DAE的度数?
思路:去掉条件AB=AC,我们不再知道∠BAD和∠EAC分别是多少度,但由等边对等角可知∠BAD+∠EAC=∠B+∠C=180°-120°=60°.
所以∠DAE=∠BAC-(∠BAD+∠CAE)=120°-60°= 60°.
可见原题中的条件“AB=AC”是多余的,变式1从特殊的等腰三角形ABC推广到一般的三角形ABC,但只要保持本质属性不变,结论仍然成立.这种变式有利于学生创新思维的形成.
变式2:已知:如图2,在△ABC中,∠BAC=90°,D、E是BC边上两点,且BD=AD,CE=AE.求∠DAE的度数.
答案:∠DAE=∠BAC-(∠BAD+∠CAE)=90°-90°= 0°.
此时,AD与AE重合.
变式3:已知:如图3,在△ABC中,∠BAC=60°,D、E是直线BC上两点,且BD=AD,CE=AE.求∠DAE的度数.
答案:∠DAE=(∠BAD+∠CAE)-∠BAC=120°-60°=60°.
变式2、3不断地变换条件的层次,将原题条件∠BAC=120°分别变为∠BAC=90°、∠BAC=60°,而且变式2、3强调了∠DAE与∠BAD+∠CAE、∠BAC的关系.这样不但活跃了学生的思维,还将知识、能力和思维方法在更多的新情境中反复渗透,达到了深化、升华的效果.
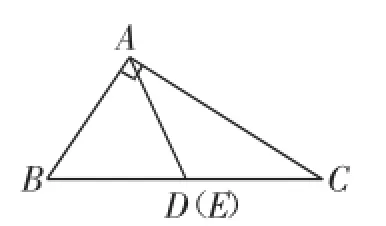
图2

图3
二、条件一般化,发现一般规律
“一般化”是构造变式题的一种重要方法,如果∠BAC的度数未知,那么∠DAE与∠BAC有何关系?于是,我们得到如下变式:
变式4:已知:在△ABC中,∠BAC=α,点D、E是直线BC上的两点,且BD=AD,CE=AE.求∠DAE的度数.
解析:因为BD=AD,所以∠BAD=∠B.同理可得∠CAE=∠C.
(1)当0°<α<90°时,
∠DAE=(∠BAD+∠CAE)-∠BAC=(∠B+∠C)-∠BAC=(180°-α)-α=180°-2α.
(2)当90°≤α<180°时,
∠DAE=∠BAC-(∠BAD+∠CAE)=∠BAC-(∠B+∠C)=α-(180°-α)=2α-180°.
综上可得:∠DAE=|180°-2α|.
变式4实际上是对前三个变式的归纳总结,变常量为变量.对于上述演变过程,我们可以利用几何画板动态展示给学生看.以课本例题为“钥匙”,通过改变条件,引申探究,加深学生对基础知识的掌握,可以提高学生自觉钻研书本例、习题的积极性.
三、改变背景,训练思维
变式5:已知:如图4,在△ABC中,∠BAC=120°,D、E是直线BC上两点,且AB=BD,AC= CE.求∠DAE的度数.
解析:因为AB=BD,所以∠BDA=∠BAD.同理可得∠AEC=∠CAE.又因为△EAD的内角和为180°,所以∠AEC+∠BDA+∠EAD=∠CAE+∠BAD+∠EAD=180°.∠BAD+∠CAE=∠BAC+∠EAD=120°+∠EAD.
因此120°+2∠EAD=180°,则∠EAD=30°.
在解题教学的思维训练中,通过改变问题背景进行变式训练是一种很有效的方法.通过改变条件,可以让学生对不同条件的情况作出正确的分析;通过改变结论可以培养学生推理、探索的思维能力,使学生的思维更加灵活和严密.类比以上变式,引导学生自主参与变式,能不能使条件一般化“令∠BAC=α”,对参数α进行讨论,得出一般规律?学生探究有困难时,可适当予以提示:点D、E可以在线段BC上,也可以在其延长线上,甚至可以重合.最后,利用几何画板向学生演示动态变化的过程.
变式6:已知:在△ABC中,∠BAC=α,D、E是直线BC上两点,且AB=BD,AC=CE.求∠DAE的度数.
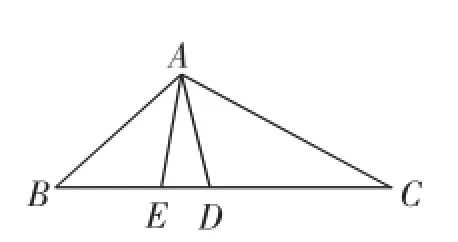
图4
四、因果互换,逆向思维
把∠DAE与∠BAC的地位交换,即∠DAE的度数是已知的,其他不变,是否可求∠BAC的度数?
变式7:在△ABC中,D、E是直线BC上两点,且BD= AD,CE=AE,∠DAE=60°.求∠BAC的度数.
解析:因为BD=AD,所以∠BAD=∠B.同理可得∠CAE=∠C.
(1)当∠BAC为钝角时(如图5),因为∠BAC=∠BAD+∠EAD+∠CAE,∠EAD=60°,所以∠BAC=∠B+∠C+60°.又因为△ABC的内角和为180°,所以∠B+∠C+∠BAC= 2(∠B+∠C)+60°=180°,则∠B+∠C=∠BAD+∠CAE=60°,则∠BAC=120°.
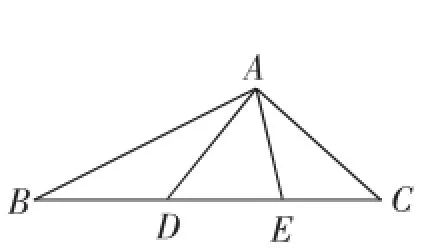
图5
图6
(2)当∠BAC为锐角时:
①当D、E其中一点在线段BC上,另一点在BC的延长线上时(如图3).因为∠EAD=∠EAC+∠CAD=60°,△ABC的内角和为180°,所以∠B+∠BCA+∠BAC=180°=∠B+∠BCA+∠BAE+∠EAC=∠B+2∠BCA+∠BAE,则180°+∠EAD=∠B+2∠BCA+∠BAE+∠EAC+∠CAD= 2(∠B+∠BCA)=240°,所以∠B+∠BCA=120°,则∠BAC= 60°.
②当D、E两点都在线段AC的延长线上时(如图6).∠EAD=∠EAB+∠BAC+∠CAD=60°,∠ABC=∠BAD=∠BAC+∠CAD,∠ECA=∠CAE=∠CAB+∠BAE.又△ABC的内角和为180°,即∠ABC+∠BCA+∠BAC=180°,所以180°+∠EAD=∠ABC+∠ACB+∠BAC+∠EAB+∠BAC+∠CAD=2(∠ABD+∠ECA)=240°.故∠ABD+∠ECA=120°,则∠BAC=60°.
综上可得,∠BAC=60°或∠BAC=120°.
逆向变式,可以培养学生的创造性思维.分类讨论,可以锻炼学生思维的严谨性.
课本上的例题、习题都是教材编写者精心编排的,教师应该扎根课本,抓住知识的本质,对课本例题、习题进行多角度的变式教学.从而“把冰冷的美丽化为火热的思考”,既能减轻学生课业负担,也能增强课堂教学的有效性,不断提高学生的思维能力.

