用相关思维破解“多点联动”型最值题的DNA*

☉湖南常德市芷兰实验学校初中部 陈金红

用相关思维破解“多点联动”型最值题的DNA*

☉湖南常德市芷兰实验学校初中部 陈金红

因果思维即逻辑线性思维，干净利索，但在解题教学中给学生一种“高冷美”的错觉，上课时听得懂但很难自由活用，实乃“知其然但不知其所以然”之常态.如何破解？先看一个“猜字灯谜”：点点成金！用数学的视角看，即求在条件“点点”运动下的“金”的原像，逆思维抽取两点不难得知“全”字即为所求的字谜！这样得出显然不是使用严格的逻辑推断，而是使用了有关联的但合情合理的联想，即裴光亚老师所言的“相关思维”，相关思维更“关乎”解题者内心的冲动、直觉与直观，“联动”更为自然和自由，运用其破解中考热点“多点联动”型最值题作用明显，下面给出具体例子.

例1（武汉2013年中考数学第16题）如图1，E、F是正方形ABCD的边AD上两个动点，满足AE=DF，连接CF交BD于点G，连接BE交AG于点H，若正方形的边长为2，则线段DH长度的最小值是____.

先看几个特殊位置.

（1）E点与A点重合时，显然此时F点与D点亦重合（初始状态），见图2，DH=AD=2.

（2）点E与边AD的中点重合时，“AE=DF”，故点F与边AD的中点也重合！见图3，很难直接看出DH的具体大小数值！但可以看出H不在边AD上运动了！

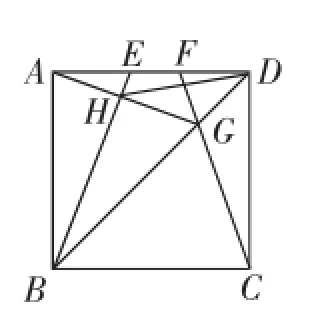
图1

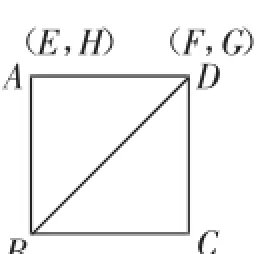
图2

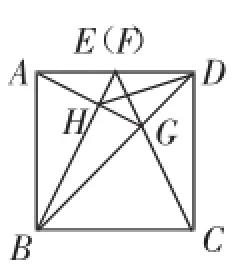
图3

图4

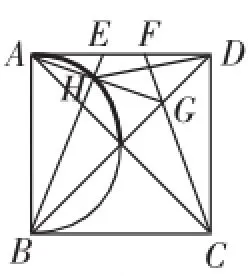
图5

（3）当点F与A点重合时，显然此时E点与D点亦重合；此时点H恰为正方形的中心即对角线的交点！见图4，简单计算即可知

结合上面3个特殊位置的定点分析，把这三个定点位置直觉连起来“颇似”一个圆上的一段弧（如图5）（特例下的猜想）？！

一般情形相关思维：

点F运动（点E亦同步运动，因为AE=DF），此时定线段BD与动线段CF的交点G也会随之运动，即线段AG也是动线段，它与动线段BE的交点H必是动点，从而线段DH必是动线段，于是它必有一个大小范围，即可知必取得一个最小值！但从中发现先有G动，再有H动，从而DH变化！

分析点G的运动路径（轨迹）：始终在线段DB上运动，起点在D位置，终点在对角线的交点P位置！

分析点H的运动路径（轨迹）：结合上面（1）（2）（3）直觉得出是一个圆上的一段弧，从（1）（3）两个特例位置发现H是一个直角顶点，于是猜想H在以AB为直径的圆上运动，见图6，即证明∠1+∠4=90°.

显然，由AB=CD，∠BAD=∠CDA=90°，AE=DF，可知△ABE≌△DCF（SAS），于是有∠1=∠2.由AD=DC，∠ADG=∠CDG=45°DG=DG，可知△ADG≌△CDG（SAS），于是有∠3=∠2.则∠1=∠3.又∠3+∠4=∠BAD= 90°，于是得∠1+∠4=90°，则∠AHB=90°.于是确认猜想：H的运动路径（轨迹）是以AB为直径的圆（圆O）的的一段弧（弧AP），见图7.

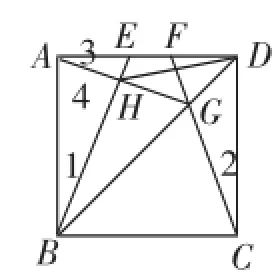
图6

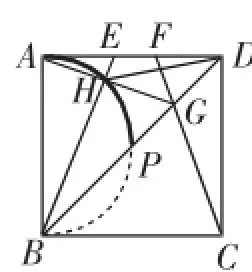
图7

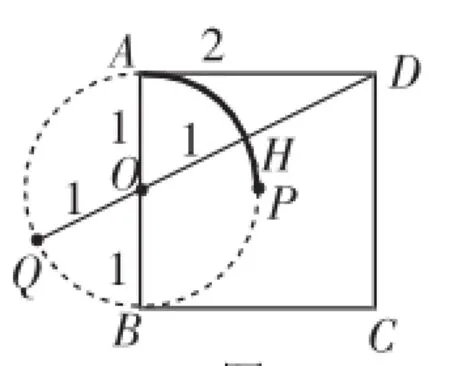
图8

最后用基本经验模型：见图8，由圆外一点（如点D）向已知圆（如圆O）引割线，过圆心和圆第一次的交点线段是最短的（如线段DH），过圆心和圆第二次的交点的线段是最长的（如线段DQ）！

借用胡适之说“大胆假设，小心论证”，数学中的假设来自于大量特例引起的冲动认知，提出假设即猜想，在放眼一般给出特例导向下的本质规律的探求即推证猜想，把自己的科学小心变为被说服者的科学放心！于是有：特例处猜想，一般推本质，相关思维即可破解此类几何最值问题的DNA即“动点轨迹”！

例2如图9，边长为3的菱形ABCD中，∠ADC=60°，M、N分别是线段AB、BC上的两点，且BM=CN，AN与CM的交点是E，连接BE，Q是BE的中点，求AQ的取值范围.

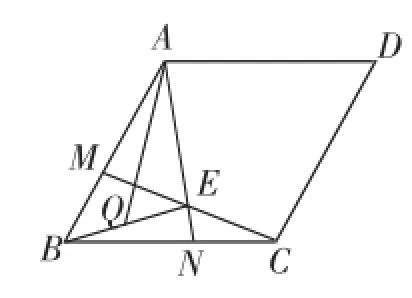
图9

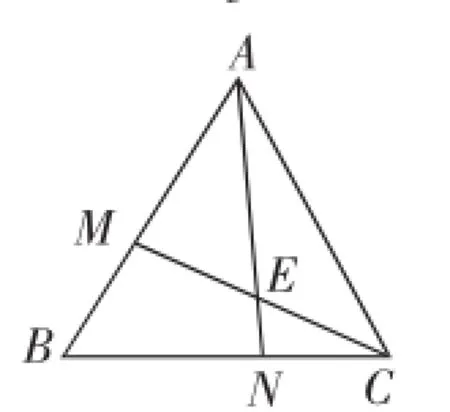
图10

（一）准备工作.

读题发现：已知菱形是两个正三角形拼合形成的.结合基本经验联想到：

（1）正三角形的特殊性质，如高、中线、角平分线均相交于一点，交点到对边的距离即内切圆的半径（r），交点到顶点的距离即外接圆的半径（R），且R=2r等若干结论的相关联想.

（2）熟悉的常规习题，见图10，已知正△ABC中，BM= CN，连接AN、CM相交于点E，有很多有价值的数学结论，如全等、相等的角、相等的线段、比例线段、“弦切角等于夹弧所对的圆周角”、与圆有关的切线和圆的模型与结论.

（二）探究工作：相关思维.

先看几个特殊位置.

M点与B点重合时，N点与C点亦重合（初始状态），见图11，此时AN、CM的交点E落在了点C位置，于是BE的中点即BC边的中点Q，于是AQ等于正△ABC的高，即AB·

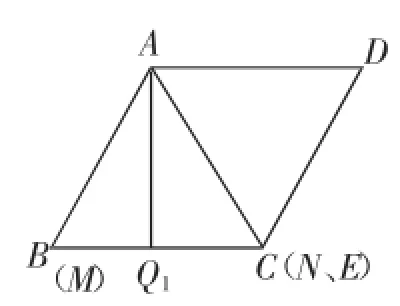
图11

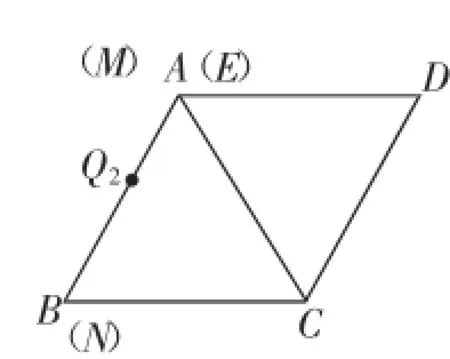
图12

M点与A点重合时，N点与B点亦重合（终结状态），见图12，此时AN、CM的交点E落在了点A位置，于是BE的中点即BA边的中点Q，于是AQ等于正△ABC的边长的一半，即

把上面的分析与原题图合成，见图13，“直觉”得出（垂足）中点Q1、Q2和普通中点Q在以正△ABC两高交点O为圆心、半径为OQ1（或OQ2，等于正△ABC高的的圆的一段弧Q1QQ2上！理论根据是什么？关键是要证明出点Q满足条件OQ=OQ1（或OQ2），因为“如果一个点到圆心的距离等于圆的半径，那么这个点就在这个已知圆上”！在此基础上“绞尽脑汁”仍无济于事、无力回天！但这么多的“中点”相关联想三角形的“中位线”是否是一线生机、一点火花、一粒种子！？

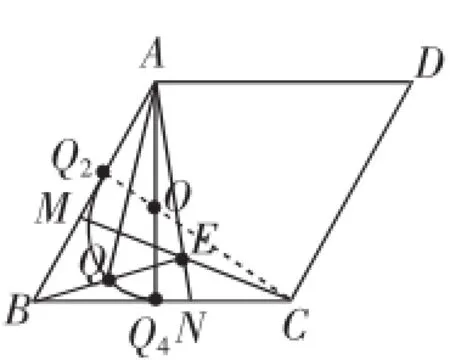
图13

回到“原点”相关思维：点Q来源于线段BE的中点，而点E来源于动线段AN、CM的交点，线段AN和线段CM源于点M和点N的运动，注意到点A、B、C是定点，只有点M、N、E、Q是动点！把点E的模型（或点E的“DNA”）弄明白了的话必可“直觉”得出点Q的模型（或点Q的“DNA”）本质！于是作相关讨论.

分析点M的运动路径（轨迹）：始终在线段AB上运动；分析点N的运动路径（轨迹）：与点M同步，始终在线段CB上运动.

分析点E的运动路径（轨迹）：结合上面图11、图12点E的特殊位置：点E与点C重合、点E与点A重合；还有一个特殊位置见图14，点E与“正△ABC两高的交点O”重合时，“直觉”得出点E在一个圆的一段弧上运动！

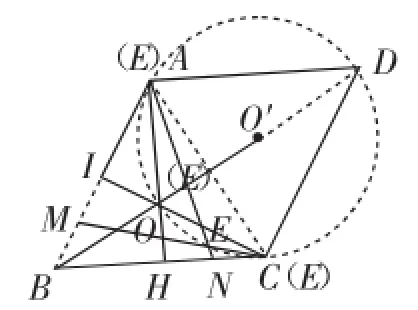
图14

为什么点E的运动路径是：在一个圆的一段弧上运动呢？始终有结论△ACN≌△CBM（SAS），始终有∠BCM=∠CAN，相关联想到“弦切角等于夹弧所对的圆周角”即直线（BC）与圆（圆O′）相切的数学模型！△ACE的外接圆的圆心必在线段AC的垂直平分线上，即在已知菱形的对角线BD上，不难和正△ABC类比得出此圆心在正△ADC两高交点O′处，BC是圆O′的切线（其中C为切点），同理可证BA是圆O′的切线（其中A为切点），见图14，于是半径O′C=O′A=正△ADC高的点E在以点O′为圆心为半径的圆上的一段弧上.

最后分析点Q的运动路径（轨迹）：

不难知相关思维起到了回到“原点”、“饮水思源”的战略高度的作用！

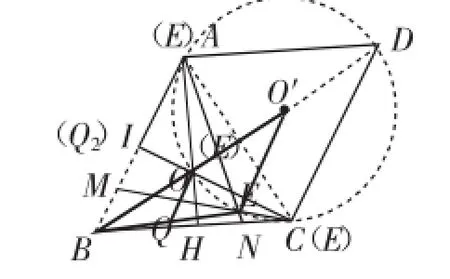
图15

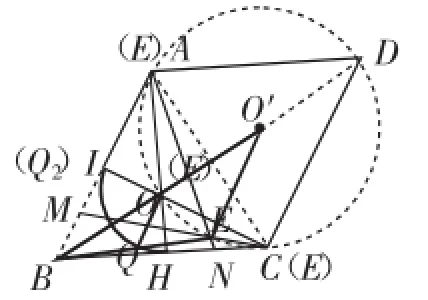
图16

最后用基本经验模型：见图16，从圆外一点（如点A）向已知圆（如圆O）引切割线，过圆心和圆第一次的交点（不是题目中点Q的位置故舍之）的线段是最短的，过圆心和圆第二次的交点的线段是最长的（如线段AQ=AH，即△ABC的高

根据Q点的运动路径，可知最短的线段AQ应该是切线长AI（边长的一半.即

（三）具体解答线索.

先得出点E的运动路径是圆弧，从而找到圆心O′.

再构造图16中△BEO′的中位线模型，再次确认线段BE的中点Q的运动路径也是圆弧.

最后运用基本经验模型“由圆外一点向已知圆引切割线，过圆心和圆第一次的交点的线段是最短的，过圆心和圆第二次的交点的线段是最长的”，得出线段AQ的取值范围！

类似中考试题：

（1）见图17，正△ABC的边长为6，点E从B向终点C运动，同时点F从C向终点A作等速运动，到各自终点后停止，运动过程中线段AE、BF交于点P，H是线段BC的中点，则线段PH的最小值为（）.

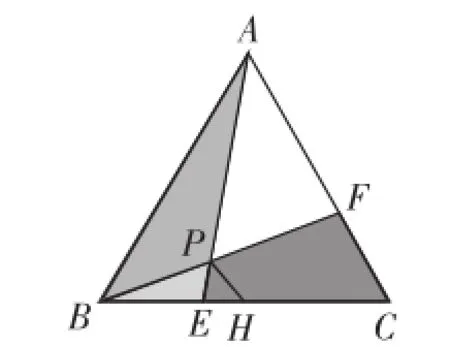
图17

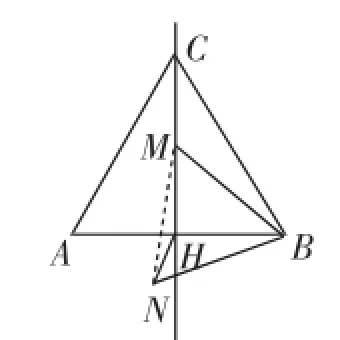
图18

（2）见图18，正△ABC的边长为3，M是高CH上一动点，连接BM，将线段BM绕点B逆时针旋转60°得到线段BN，再连接HN，则点M在运动过程中线段HN长度的最小值为（）.

（四）反思工作.

捋一捋相关思维用于解题教学的一般程序：先对“要求的动点”特殊位置作确定性分析与一般猜想，引起多个直觉、构造模型；再对直觉和模型“追问道理”，“联动”点的“子父辈”关系即先“爷”后“父”最后“儿女”辈的递进其实是运动路径的过程分析，而这个路径其实就是“动点”的运动“轨迹”即动点的“DNA”本质分析.

同时我们还发现“基本经验模型”和“熟悉的常见习题”是我们思维“跳跃”的最佳“支点”，为我们缩短“思维长度”作出了“不可磨灭”的贡献和作用.

代数法用数量彰显自己的长处，向目标夯实放心前行，几何方法用直观轨迹彰显自己的优点，揭示问题的本质.无论代数还是几何方法，都是数学思维方法，但更多的是用的逻辑思维，而逻辑思维是线性思维，更易掉“链子”、做题时易“短路”，结合上面“多点联动”型问题分析发现：相关思维除了具有“片段、区间”的因果逻辑，还有整体思考上的“人文性”，我调侃因果思维是相关思维的“极限”，“相关思维”有时显得更有用、有效、好使！经验表明它是破解“多点联动”型最值题的DNA的良策，尽管可能是个性化的！因此我有个小小的呼吁：让几何基本“轨迹”重新回到初中数学教材的“怀抱”中来！为数学学科核心素养的有效落地赋予更好的“素材”！

1.裴光亚.大数据：教学研究的曙光［J］.中学数学教学参考（中），2016（12）.

2.陈金红.数学教学我特有的五句话［J］.数学教学研究，2016（12）.

3.陈金红，郭作华.自然生成道理追问——从一道填空难题谈起［J］.河北理科教学研究，2016（1）.

4.陈金红等.“同一法”如何处理更有效——谈学科核心素养的基本观点［J］.中学数学（下），2016（5）.

*本文系全国教育科学"十二五"规划2013年度教育部规划课题“生命课堂视野下的教学案例研究”（课题编号：FHB130512）的成果之一.