一图一世界，一法通一片

☉江苏如皋市东陈镇雪岸初级中学 陶成龙

一图一世界，一法通一片

☉江苏如皋市东陈镇雪岸初级中学 陶成龙

众所周知，中考数学压轴题难度偏大，承载着区分数学水平与选拔人才的功能.这一类题重点考查学生灵活运用数学知识和思想方法解决数学综合问题的能力.笔者有幸参与了2015年南通市中考数学网上阅卷工作，当时评阅的正是压轴题第28题，发现此题的命题思路似曾相识.笔者查阅研究了近5年南通市中考数学试卷中的压轴题，发现此题与2012年南通中考第28题、2014年南通中考第28题和2015年南通中考第10题似乎在演“连续剧”，的确有点儿“纯属巧合”.现撰文回顾，供大家参考.

一、试题呈现

题目：（2015年南通中考第28题）已知抛物线y=x2-2mx+m2+m-1（m是常数）的顶点为P，直线l：y=x-1.

（1）略；

（2）当m=-3时，抛物线与x轴交于A、B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图1），求点M的坐标；

（3）略.

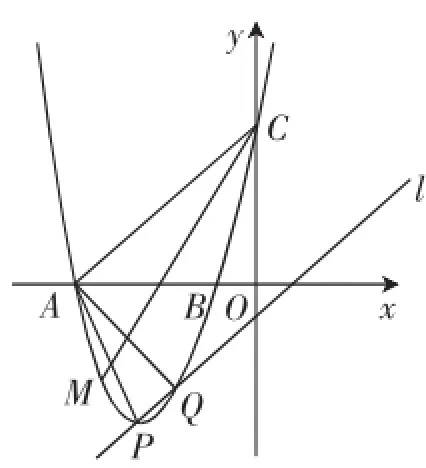
图1

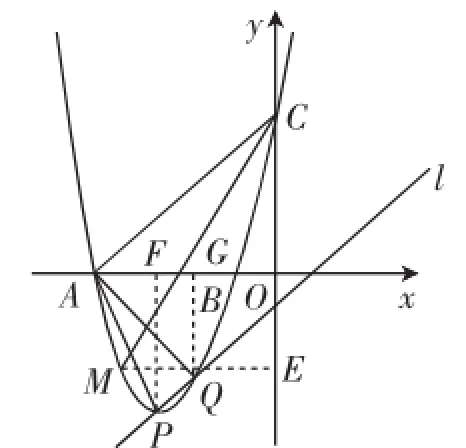
图2

参考答案：（2）如图2，当m=-3时，抛物线的解析式为y=x2+6x+5，可以求出A（-5，0）、C（0，5）、P（-3，-4）、Q（-2，-3），作ME⊥y轴于E，PF⊥x轴于F，QG⊥x轴于G，证明Rt△CME∽Rt△PAF，利用相似得x2+6x+5），则解得x1=0（舍去），x2=-4，于是得到点M的坐标为（-4，-3）.

点评：本题参考答案添加了3条辅助线，而添加辅助线对学生来说比较困难，更何况添加了3条之多，解法有点儿唐突、生硬，其次发现并证明Rt△CME与Rt△PAF相似并不容易.在阅卷的过程中，考生的答题情况与我预估的情况差不多，采用这种方法解题的少之又少，当时我一边阅卷一边在想，解决这个题目有没有更好的方法？有没有一种解法是学生能够自然而然想到的？学生根据A（-5，0）、P（-3，-4）、Q（-2，-3）能够发现△AQP为直角三角形，而且PQ∶AQ=1∶3，所以不妨在x轴上截取OE（如图3），使得OE=3OC=15，这样就使得∠CEO=∠PAQ，从而易证△CAE∽△DAC，根据AC2=AD·AE可以求得AD=2.5，从而可以求出直线CD的解析式y=2x-5，根据直线CD与抛物线的交点为点M，通过联立方程可以求出点M的坐标为（-4，-3）.现笔者简要介绍一下这个方法的来源，以及撷取3道南通中考压轴题谈谈此解法的应用.

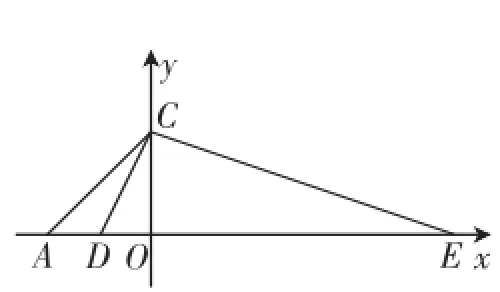
图3

二、溯本求源

1.认识基本图形.

新课程理念强调：数学教学要从学生已有的知识和生活经验出发，让学生亲身经历将数学问题抽象成数学模型并进行解释与应用的过程.对于射影定理的基本图形及结论师生再熟悉不过了（如图4），如果将其题设∠BAC=∠ADC=90°再进一步一般化，改成∠DAC=∠ABC，那么就得到几何中最常见的基本图形（如图5），也就是说射影定理的基本图形其实是这一基本图形的特殊情况（暂且称作“母子相似图”）.这个几何基本图形直观形象、结论简洁明了，对于解决相关压轴题具有其他方法不可替代的优越性，可以起到化繁为简、化难为易的独特效果.

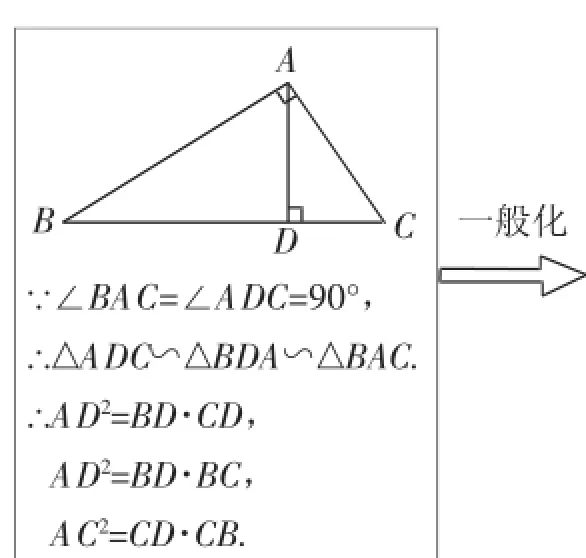
图4

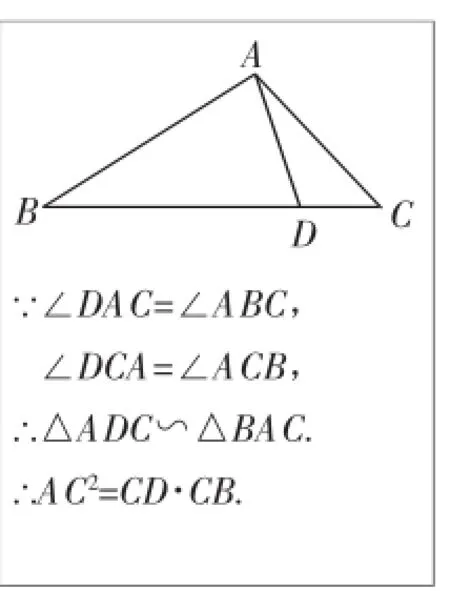
图5

2.辨析基本图形.

例1（2015年南通中考第10题）如图6，AB为⊙O的直径，C为⊙O上一点，弦AD平分∠BAC，交BC于点E，AB=6，AD=5，则AE的长为（）.

A.2.5 B.2.8

C.3 D.3.2

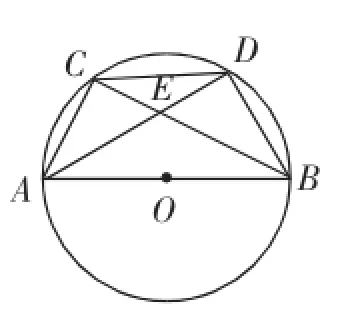
图6

分析：由勾股定理先求出BD的长，由弦AD平分∠BAC，得到∠CBD=∠DAB，再利用“母子相似图”这一基本图形得到△ABD∽△BED，根据DB2=DE·DA可解得DE的长为2.2，则AE=AD-DE=5-2.2=2.8，故选B.

点评：此题主要考查三角形相似的判定和性质及圆周角定理，解答此题的关键是学生能从纷繁复杂的几何图形中分辨识别出这一基本图形，从而利用其结论即△ABD∽△BED求出正确答案.波利亚曾说过：“解题的成功，要靠正确地转化.”有的时候，压轴题不会具有明显的这一基本图形的结构特征，需要学生基于对这一基本图形的深刻认识与理解，通过添加恰当的辅助线，创造性地构造这一基本图形来解决问题.

3.构造基本图形.

例2（2012年南通中考第28题）如图7，经过点A（0，-4）的抛物线+bx+c与x轴相交于点B（-2，0）和C， O为坐标原点.

（1）略；

（2）略；

（3）设点M在y轴上，∠OMB+∠OAB=∠ACB，求AM的长.

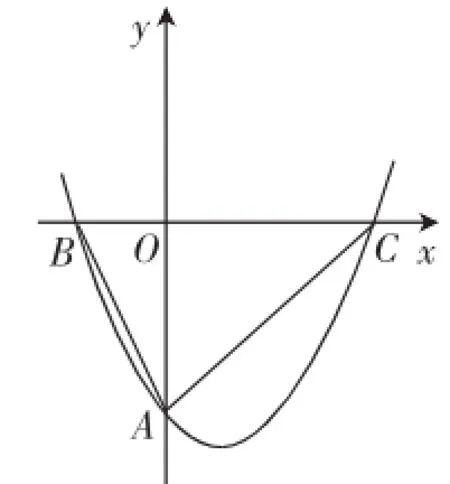
图7

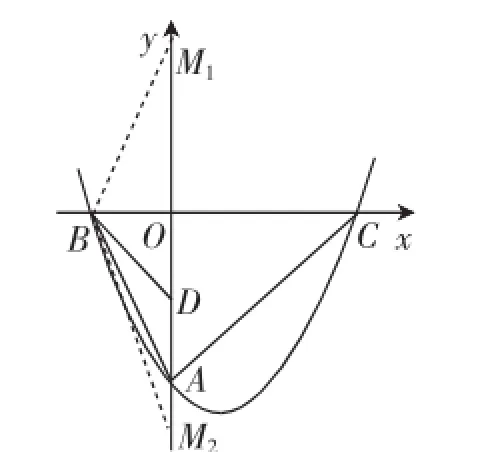
图8

分析：如图8，取OA的中点D，连接BD，则OB=OD=2，∠OBD=∠ODB=45°.因为∠DBA+∠OAB=45°，所以在y轴上找一点M1，使得∠OM1B=∠DBA.从而△DAB∽△BAM1，即AB2=AD·AM1，从而求得AM1=10.根据对称性，AM2=2，故AM的长为2或10.

例3（2014年南通中考第28题）如图9，抛物线y= -x2+2x+3与x轴相交于A、B两点，与y轴交于C，顶点为D，抛物线的对称轴DF与BC相交于点E，与x轴相交于点F.

（1）略；

（2）略；

（3）设P为x轴上一点，∠DAO+∠DPO=∠α，当tan∠α= 4时，求点P的坐标.

图9

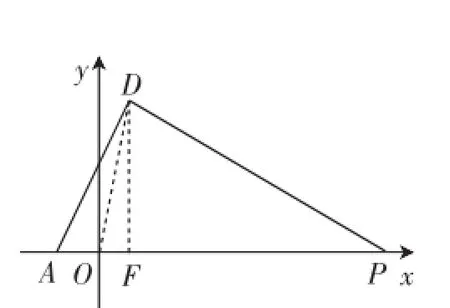
图10

分析：C（0，3）、A（-1，0）、B（3，0）、D（1，4），则tan∠DOF=4，得出∠DOF=∠α.然后根据三角形外角的性质即可求得∠DPO=∠ADO，进而求得△ADP∽△AOD，得出AD2=AO·AP，从而求得OP的长，进而求得P点的坐标.再根据对称性，求得满足题意的点P的坐标为（19，0）和（-17，0）.

点评：这两道压轴题均是在分析角与边的内在关系的基础上，通过添加一定的辅助线构造出完整的基本图形，进而应用这个基本图形的性质及相关结论解决问题.可见教师在平时的教学过程中帮助学生提炼一些典型的数学模型，有助于学生在解决难题时形成思路，探得方法，从而有效地提高解题速度和得分率.

中考压轴题演绎着万千世界，命题者往往将一些基本图形进行改编与重组，但其背后运用的数学思想方法却是相通的.作为教师，在中考复习时，要帮助学生从中考题海战术中走出来，培养学生以一图识万图的能力，这样才能使学生达到学一法，会一类，通一片的境界.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

2.［美］波利亚，著.怎样解题［M］.阎育苏，译.北京：科学出版社，1982.

3.曹志迅.“一线三等角”：客从何处来？——以“相似三角形”习题课为例［J］.中学数学（下），2016（4）.