例谈数学解题研究的几个视角

☉江苏苏州市苏州工业园区第十中学 袁丽华

例谈数学解题研究的几个视角

☉江苏苏州市苏州工业园区第十中学 袁丽华

对于数学教师而言，很多时间一直在做着数学研究：你要上好一节课，就要研究教材.一名数学教师研究的方向众多，概括起来有：一是课本题目，二是各种试卷中的题目，有修为的可以研究杂志上的题目，更加具有能力的可以自己提出数学问题.下面就从解决数学问题的一些常规方向出发，具体谈一谈.

视角一：课本研究

课本习题研究是我们的基本功，课本典型例题的解读是校本研究的一种手段.笔者结合自己的一些想法，来分析一下这个问题.

案例1：（苏教版七年级数学下P35习题）如图1，小明从点A出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°……照这样走下去，他第一次回到出发地A点时，一共走了多少米？

解答：对于这个题目，由多边形外角和公式，可以得到小明走过的路线为正十二边形的周长，因此小明共走了120m.

为了得到正多边形，向左转的角度最大值为120°，是360的约数，我们提出如下问题：向左转的角度大于120°，如144°、150°——情况怎么样呢？开始我没有意识到这是一个精彩的问题，当进行不断的探索和发现以后，会有很多意外的收获.会有哪些收获呢？可以对课本问题进行一系列的改编.

变式1：小明从点A出发，沿直线前进10米后向左转144°，再沿直线前进10米，又向左转144°……照这样走下去，他第一次回到出发地A点时，一共走了多少米？

变式2：小明从点A出发，沿直线前进10米后向右转72°，又前进10米后向左转144°；再沿直线前进10米后向右转72°，又前进10米后向左转144°……照这样走下去，他第一次回到出发地A点时，一共走了多少米？

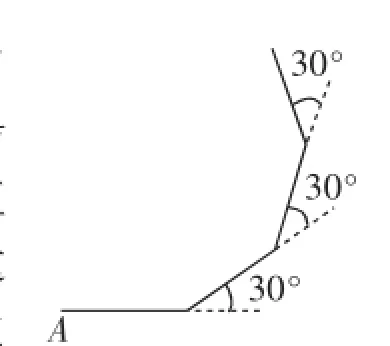
图1

通过对问题的不断改编，可以对问题进行深入研究，从而有可能得到更为丰富的结论.

视角二：试卷研究

各种试卷往往承载老师研究的智慧，关注并研究这些试题往往会得到意想不到的收获，尤其从试卷的命制过程中，我们往往会得到一些新的灵感和启发，从而促进日常教学.

案例2：（2016年重庆）如图2，以AB为直径、点O为圆心的半圆经过点C，若AC=，则图中阴影部分的面积是（）.

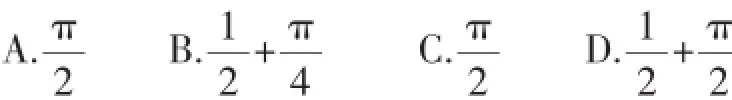
图2

剖析：这是一个被许多中考模拟试卷采用的题目，其解答几乎千篇一律，解这个题目的关键是分析出点C随点A运动所形成的图形是什么.如果从问题本质和根源出发，我们需要回到课本中去探究，本题考查扇形面积的计算：圆面积公式和扇形.求阴影面积常用的方法：①公式法；②和差法；③割补法.求阴影面积的主要思路是将不规则图形的面积转化为规则图形的面积.先利用圆周角定理得到∠ACB=90°，则可判断△ACB为等腰直角三角形，接着判断△AOC和△BOC都是等腰直角三角形，于是得到S△AOC=S△BOC，然后根据扇形的面积公式计算图中阴影部分的面积.

视角三：错题角度

错题是学生在解答过程中错误率较高的问题，对于这样一类问题，我们需要格外关注，因为只有抓住了这样的问题，才能帮助学生真正提高成绩，从而收获信心，提升数学的兴趣和能力，下面来看这样一个经典的错题.

案例3：阅读下列材料：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫作点的“特征线”.例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=-x+4.

问题与探究：如图3，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线经过B、C两点，顶点D在正方形内部.

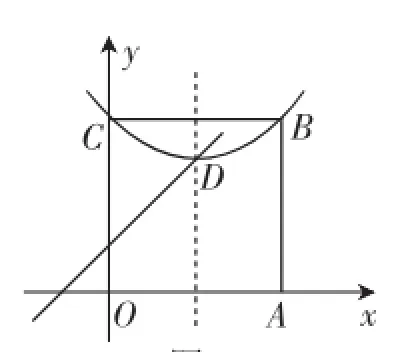
图3

（1）直接写出点D（m，n）所有的特征线；

（2）若点D有一条特征线是y=x+1，求此抛物线的解析式；

（3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？

解：（1）由点D（m，n），得点D（m，n）的特征线是x=m，y=n，y=x+n-m，y=-x+m+n.

（2）点D有一条特征线是y=x+1，则n-m=1，则n=m+1..由四边形OABC是正方形，且D点为正方形的对称轴，D（m，n），得B（2m，2m），则解得m=2，则点D（2，3）.

（3）如图4，当点A′在平行于y轴的D点的特征线上时，根据题意可得D（2，3），则OA′=OA= 4，OM=2，则∠A′OM=60°，则∠A′OP=∠AOP=30°，则MN=则抛物线需要向下平移的距离

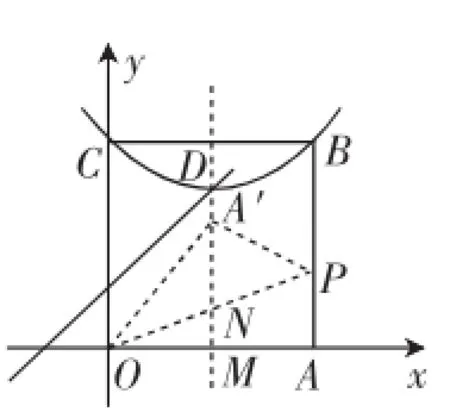
图4

如图5，当点A′在平行于x轴的D点的特征线上时，由顶点落在OP上，得A′与D重合，则A′（2，3）.

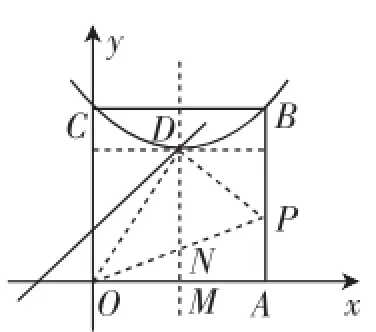
图5

剖析：对于错误原因，我们往往需要进行细致分析，找到问题的症结所在，从而突破问题带给学生的障碍，最终得出正确的结论.从卷面上来看，这是一个10分的问题，实际得分情况是不能令人满意的，学生除了第一问，实际得分仅仅在2分以内，错误率超过了80%，从此题的情况而言，有阅读障碍的数学阅读类难题对于学生思维的影响是巨大的，学生非常容易被实际的问题形态吓到，从而无法找到真正解决这一问题的思路和方法.对于最值问题，在初中阶段本身是难点，找到突破口尤为重要，教师针对这样的问题，需要从自身角度出发，帮助学生进行细致入微的分析，实现对问题的解读和突破.

视角四：动笔写作

动笔写作，其实是一种最好的归纳问题的思路和方法.动笔的理由很简单，有读书的体会，有教学的心得，有来自学生的智慧之花，也有对于学生典型错误的剖析，如此种种，某一时刻的感想，或许写不成一篇论文，但是，你把它通过你的笔端写下了，积溪流成大河.其实，多动笔，对于教师来说是有百利而无一害的，通过动笔的过程，教师在形成自身思考过程的前提下，能够帮助自己形成和完善观点，找到解决问题的方法，从而更加系统性地认识问题.因此，学习的方法上要有自己的看法，敢于挑战名题，改造或者引申名题，也可以给出自己的新的证明方法，这都是教师自身的一种挑战和创新.

综合以上的一些情况，问题研究的方向是多维和多元的，教师只要自身时时留意，处处用心，就能够发现更多的视角和方向，体会更多的乐趣和感悟.