强调图形方法作用,促进知识高效接受
☉江苏宜兴市楝树中学 杨燕
强调图形方法作用,促进知识高效接受
☉江苏宜兴市楝树中学 杨燕
在数学知识学习与具体问题分析的过程中,经常会运用到不同种类的思想方法.具体至初中阶段的数学教学,最值得师生加以关注的典型思想方法之一就是数形结合思想.无论哪个部分的知识学习,都少不了图形的加入.有的时候,图形的出现是为了让知识的理解更加顺畅;有的时候,图形则可以为数学问题的分析启发思路,让学生的思维清晰起来.可以说,想要实现优质高效的数学学习,不仅要时常依靠图形,更需要主动联系图形,深入挖掘图形的方法引导作用.
一、在数式中运用图形,寻找巧妙分析方法
初中是数学学习的基础阶段,其中包含了许多数与式的较为零散的内容.很多学生表示,很难以系统化的方式掌握这些知识,当遇到灵活变化的问题时,更是无法总结出规律性的方法.因此,数、式的相关内容虽然所占据的比重不算太大,却为学生制造了不小的学习困难.这时,图形方法的适时介入便开始显得愈发重要了.例如,在数轴内容的学习过程中,学生曾经遇到过这样一个问题:实数a、b在数轴上的位置如图1所示,那么的化简结果是什么?这个问题的解答方向很明确,就是要通过数轴图形来分析出a和b的大小关系,进而对上述代数式进行化简.通过图形分析,学生不仅要看出a<0、b>0这些显而易见的信息,还需要看到a<b的大小关系.在此基础上,才能准确地将根号和绝对值符号去掉,得到正确答案.这个问题也给了学生很多启发,很多学生表示,对于类似的问题,不仅可以从正向分析图形,寻找数量关系,还可以反过来,以图形的方式呈现已知条件中的内容,寻找巧妙分析的方法.在图形的引导之下,以数和式为背景的填空、选择等小题,解答起来就方便、简洁了许多,相应的学习效率自然也显著提升了.
虽然每个数式问题都具有不同的解答方法,但是,图形方法的适用却是同一的.当学生遇到了难以入手分析,或是计算起来比较复杂的问题时,不如从抽象的理论转向生动的图形,以这种明确的方式来表现已知条件中的各种关联.通过图形的巧妙运用,学生经常可以从中收获许多解答问题的捷径,为高效学习提供很大帮助.
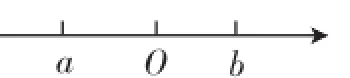
图1
二、在方程中运用图形,直观分析特点内涵
谈到方程,学生的眼前大多会出现一串串数字、字母与符号的组合,很少有人会将之与具体的图形联系起来.然而,若能够将图形恰当地运用于方程问题的解答之中,将会显著提升分析与解题的效率,正确率也会增加许多.
例如,在对二元一次方程组的内容进行学习时,学生曾经遇到了这样一道选择题:用图像法解某一元二次方程组时,在同一直角坐标系中作出相应的两个一次函数的图像(如图2所示),则所解的二元一次方程组是().
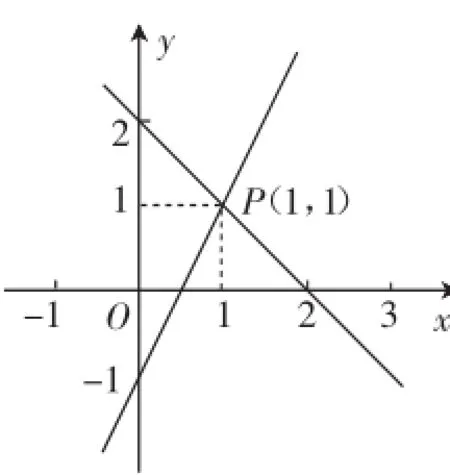
图2
这个问题的解答难度并不算大,其中的思维关键便在于由图像得出待求方程组的解为想通了这一点,只需要逐个选项代入计算验证找到正确答案.这个问题的出现,向学生明确了一个很重要的分析方法:巧妙理解图像交点的含义.找到了这个分析入口,便可以为类似问题的解答提供启发.可以说,这个问题不仅完成了方程知识的训练任务,还从一定程度上对学生开展了一次解题技巧的教学.
随着图形方法在方程问题之中的不断运用,学生对于数形结合的感悟已经逐渐超越了解题本身.在图形的辅助之下,学生开始逐步走向对于知识内容的关注,图形更像是一个引导思维具化、深入的有力工具.在提高解题效率的同时,深化学生对于理论知识的理解,可谓图形方法适用的双重价值了.
三、在函数中运用图形,细致探究规律特征
函数是初中数学中的一个重要知识组成部分,无论是基础教学阶段,还是习题训练阶段,函数都占据了数学视野的半壁江山.因此,对于函数问题的巧妙解答也就很自然地成为了教师需要关注的一个重点.在函数中运用图形,可以从两个角度加以把握,一是以图形为依据,由此分析相应的函数问题;二是在看到问题之后,通过绘制相应图形来寻找解答问题的入手点.
例如,为了帮助学生熟练掌握二次函数的细节特征,我请学生完成这样一个问题的解答:图3为二次函数y= ax2+bx+c的图像,有下列说法:(1)ac<0;(2)方程y=ax2+bx+c的根是x1=-1,x2=3;(3)a+b+c>0;(4)当x>1时,y随x的增大而增大.正确的说法是哪些?这道题目看似基础,却很细致地考查学生对于二次函数特征的掌握,且这些特征的得出都需要对图像进行有效分析.根据之前的课堂教授,学生结合所学知识,从题目所提供的图像中抓住了该二次函数的开口方向、与x轴和y轴的交点数量及位置、函数图像对称轴所在位置等信息,得出了系数a、b、c之间的关系,进而很顺利地确定了说法(1)、(2)、(4)是正确的.这样的训练,让学生能够从图形中将其中所蕴含的有价值条件全部挖掘出来,为解题过程更好地服务.
函数与图形之间本来就存在着极为密切的联系.虽然在初中阶段,学生先后接触了许多不同种类的函数,但是,无论函数的具体形式如何,有一个特点却是相同的,那就是每个函数都有专属的图像与之对应.从函数图像当中,不仅能够看到函数的具体形态,还可以分析出数量变化趋势、系数对称特征等诸多细节,对于函数内容的把握助益颇多.作为与函数密不可分的内容,图形自然也应当在问题解答的过程中时常出现,让蕴含其中的规律特征明确展现出来.
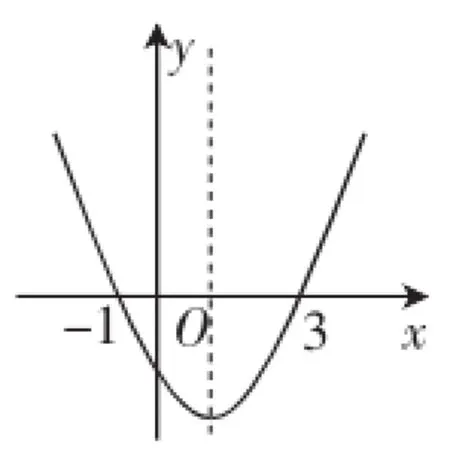
图3
四、在统计中运用图形,有效呈现数量关系
如果从图形对于题目解答作用的显著程度来讲,统计问题一定是排在前列的.从表面看来,概率统计部分的知识内容并不是难度最大的,但是,想要做到完全掌握,遇到这类问题不丢分,并不是容易的事情.很多统计问题的出现,本就是伴随着图形一起的.这便足以见得图形对于这类问题分析解答的重要性.
例如,在统计内容的教学过程中,我为学生设计了这样一道习题来深化知识理解:某报社为了解读者对于本社一种报纸四个版面的喜好情况,对读者开展了一次问卷调查,请读者们在调查中选出自己最喜欢的一个版面,并根据调查结果,绘制了一幅条形统计图(如图4①).(1)你从条形统计图中能够得到哪些信息?(2)请根据条形统计图将扇形统计图(如图4②)补全,并分别阐述二者各自具备的特点.(3)请依据两幅统计图中的信息,为报社提出一个完善建议.这个问题比较全面地考查学生的综合分析能力.它不仅要求学生能够从图形当中发现有效的信息,还要对这些基础信息进行加工、分析与计算,得到精准的当前状态.图形对于统计活动开展的作用表露无遗.

图4
对统计问题稍加观察总结便不难发现,无论是统计问题的提出,还是统计问题的分析,都离不开图形的帮助.在很多情况下,统计问题解答所需要的许多重要元素,都是隐藏在与之相对应的图形当中的.因此,在对统计内容进行教学时,笔者总是会将读图能力的提升作为一个关键的培养目标.加强了图形运用能力,无需教师过多解释,学生便能够从中得到很多解题所需的重要信息,促进知识接受的自主高效.
从上面的论述不难发现,在初中数学的知识学习当中,图形方法的适用范围是极为广泛的.的确,数学知识内容的产生本就与图形之间存在着紧密的联系.纵观各个领域的数学理论,几乎都可以通过图形的方式对之加以阐释.对具体图形进行观察分析,也常常可以从中得到数学方面的启发.二者相互促进,才构成了数学的高楼大厦,并推动其不断变换与深化.图形方法的运用,就像是为学生提供了一把金钥匙,可以让学生巧妙、准确地应对各种复杂疑难的问题,让大家的数学学习过程顺利、高效.

