图形中角的度数

◎徐洪梅

认识三角形后，大家知道三角形的内角和是180°，如果再结合三角形的特征，就能求出藏在三角形中的内角的度数。

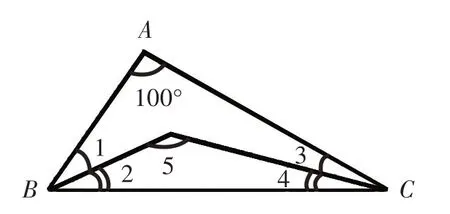
【例1】如右图，∠1=∠2，∠3=∠4，∠A=100°，求∠5的度数。

【思路分析】在△ABC 中，∠A+∠B+∠C=180°。要求∠5 的度数，先要求出∠B 与∠C 的度数和，然后再求出∠2与∠4的度数和，最后就能求出∠5的度数。

解：因为在△ABC 中，∠A+∠B+∠C=180°，∠A=100°，所以∠B+∠C=180°-∠A=180°-100°=80°。又因为∠1=∠2，∠3=∠4，所以∠2+∠4=80°÷2=40°，∠5=180°-（∠2+∠4）=180°-40°=140°。

【例2】如下图，D是AC边上的一点，DA=DB=DC=BC，求∠A的度数。

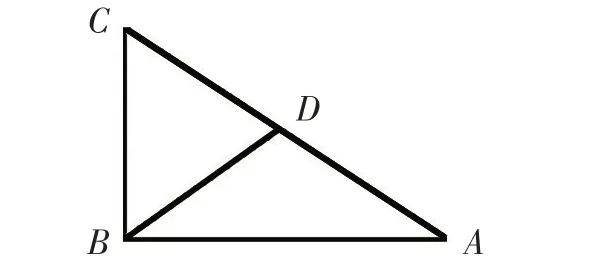
【思路分析】根据DB=DC=BC，可知△BCD 是一个等边三角形，所以每个内角的度数相等，都是60°；又根据DA=DB，可以知道△ABD是一个等腰三角形，如果知道∠ADB的度数，就能求出∠A的度数。

解：由DB=DC=BC，可以知道∠BDC=60°，∠ADB 与∠BDC 组成一个平角，所以∠ADB=180°-60°=120°。又由于DA=DB，说明∠A=∠ABD，而∠A+∠ABD=180°-120°=60°，所以∠A=60°÷2=30°。

【挑战自我】

1. 在一个直角三角形中，其中一个锐角是65°，求另一个锐角的度数。

2. 如右图，在△ABC 中，BD 是AC 边上的高，∠C=∠ABC=2∠A，求∠DBC的度数。

（扫二维码可立刻看详解，扫码仅需一元钱哟）