例谈少教多学、自主高效的数学问题设计

郑伟强

[摘 要] 农村初中数学教学中要做到“少教多学，自主高效”，必须充分利用课堂45分钟，以有效的问题串组织整堂课的教学，以学生熟悉的生活问题入手设计导入问题，以生活性、层次性为原则设计认识新知问题，以针对性、启发性、思维性为目的设计探究问题，从而激发学生的学习兴趣、引发学生积极思考.

[关键词] 少教多学；自主高效；问题设计

在农村初中数学教学中如何做到“少教多学，自主高效”，是困扰农村教师的一大难题. 由于农村学生知识面窄、在家里没有较好的学习环境，家长知识水平基本偏低，在孩子的学习上无法跟教师配合，而老师与学生接触的时间一般每天只有45分钟，因此如何做到“少教多学，自主高效”显得更为重要.

美国数学家哈尔莫斯说“问题是数学的心脏”，数学教学的过程就是引导学生解决数学问题的过程. 因此教师是否做到精心准备问题、层层深入、步步发问，是否以有效的问题串组织整堂课的教学过程，是能否达到“少教多学，自主高效”的关键. 下面笔者以华师大版初中数学八年级下册“17.2.1平面直角坐标系”为例，谈谈对这节课数学问题设计的几种做法.

以学生熟悉的生活问题入手设

计导入问题

在回顾旧知，导入新课阶段，由17.1 的问题1我们知道气温变化图可以直观地表示出不同时间的气温，反映出气温变化的规律. 像这样，函数常常可以用它的图像来表示，利用函数的图像可以幫助我们直观地研究函数.

问题1：什么是函数的图像？怎样画出函数的图像呢？

根据学生的回答，告诉学生“要画出函数的图像，可借助今天要学习的一个非常有用的工具——直角坐标系. ”

问题2：你们去电影院看电影时是怎么找座位的？

引导学生发现：因为电影票上都标有“×排×座”的字样，所以找座位时先找到第几排，再找到这一排的第几座就可以了，也就是说电影院里的座位完全可以由两个数确定下来.

总结：物体的位置可由两个数确定.

设计意图 从学生熟悉的找电影院座位入手，唤醒学生对已有知识的的记忆，激活已有的生活经验，引发学生思考，使学生产生就近联想，从而使新课的导入水到渠成.

以生活性、层次性为原则设计

认识新知问题

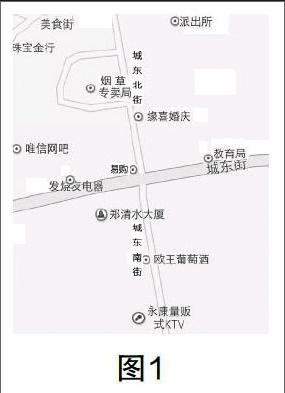
在设置情境、认识新知阶段，从学生身边熟悉的生活场景入手，从学生的最近发展区出发，层层深入设计问题，使学生经历新知的发生、发展过程. 首先出示地图（如图1，这张地图是学生非常熟悉的县城中的一部分），引导学生看地图，十字路口是易购超市，易购的正东方向40米是教育局，正西方向30米是发烧友电器商店.

问题1：你能用学过的数学模型来描述它们的位置吗？

引导学生思考讨论后得出解决方法：由于这三个地方都在笔直的城东街上，把这条街抽象为一条数轴，把这三个地方抽象为三个点，如果把易购作为原点，以向东为正方向，以1米为单位长度，可用数轴来描述它们的位置，教育局记为+40，发烧友电器商店记为-30.

问题2：易购正北方向的城东北街上35米是缘喜婚庆商店，如何描述它的位置？

引导学生思考讨论后，得到解决方案：再建一条与城东街垂直的数轴，为了方便，仍以易购为原点，以正北为正方向，以1米为单位长度，可把缘喜婚庆商店记为+35.

问题3：派出所在城东北街东边36米，在城东街北边90米，又要怎样表示它的位置？

让学生独立思考，再小组讨论，最后全班交流. 引导学生得出解决方案：在城东北街东边36米，若向横的数轴作垂线，垂足对应的数字就是+36，可用+36表示，在城东街北边90米，若向纵的数轴作垂线，垂足对应的数字就是+90，可用+90表示，规定先写横的数轴上的数，再写纵的数轴上的数，可写为（36，90）.

问题4：能把派出所的位置（36，90）写成（90，36）吗？

引导学生观察思考后发现：（90，36）是表示城东北街东边90米，城东街北边36米的位置，这不是派出所的位置. 数对是有顺序的，顺序不同则表示的位置不同.

问题5：唯信网吧在城东北街西边50米，在城东街北边27米，能用（50，27）表示它的位置吗？

引导学生思考讨论后得出：必须用（-50，27）来表示.

问题6：能统一用有序数对表示教育局、发烧友电器商店、缘喜婚庆商店的位置吗？

和学生一起讨论后发现能统一用有序数对表示它们的位置. 教育局就是在城东北街所在直线的东边40米，在横的数轴上的对应数字是+40，在纵的数轴上的对应数字是0，因此可表示为（40，0），同理发烧友电器商店记为（-30，0），缘喜婚庆商店记为（0，+35）.

归纳：老师画图并归纳讲解平面直角坐标系相关概念，如图2，像这样在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴，称为平面直角坐标系. 通常把其中水平的一条数轴叫做x轴或横轴，取向右为正方向；竖直的数轴叫做y轴或纵轴，取向上为正方向；两数轴的交点O叫做坐标原点.

回顾总结：根据刚才的合情推理发现，只要建立适当的平面直角坐标系，就可以用有序数对来表示任何一个物体的位置，从而把实际问题转化成数学模型，又把几何问题转化成代数问题（有序数对），这是多么神奇和巧妙啊！

问题7：你们知道平面直角坐标系是谁发现的吗？引导学生看课本42页阅读材料：笛卡儿的故事.

设计意图 利用学生刚在17.1 变量与函数的问题1中体会到气温变化图可以直观地表示出不同时间的气温，形象地反映出气温变化的规律，知道了函数的图像可以帮助我们直观地研究函数，因此学生迫切地想知道什么是函数的图像，怎样画出函数的图像，从而唤起学生的求知欲望，为更好地完成本节课的学习任务做好了准备. 用学生身边熟悉的地图创设情境，贴近学生的生活实际，调动学生的学习热情，发现确定点的位置是生活中经常会遇到的实际问题. 引导学生把实际问题转化为数学问题，设计问题串，引导学生先用数轴来表示点的位置，再引出在两条数轴的图形中用有序数对来表示点的位置，最后归纳出平面上任一点都可用有序数对来表示其位置. 问题由浅入深，分散难点，逐个突破，符合学生的认知规律，逐步培养学生的探究能力，为后面解决根据坐标描出点的位置、由点的位置写出它的坐标这两个难点做好准备. 最后引导学生阅读与平面直角坐标系有关的数学史，让学生感受数学家善于观察、热爱思考、追求真理的精神，培养学生的良好品格.

以针对性、启发性、思维性为目

的设计探究问题

在探究提升，深化认识知识阶段，老师提的问题应紧扣教材重点和难点，要有针对性、启发性和思维含量. 要提有思考价值的问题，才能使学生在问题的启发下、老师的引导下解决问题，深刻理解掌握数学知识的内涵.

1. 认识坐标概念，由点写坐标

让学生动手画一个平面直角坐标系，老师巡视，纠正学生画得不对的地方，若发现普遍性错误，则进行统一讲解，让学生认识并改正错误.

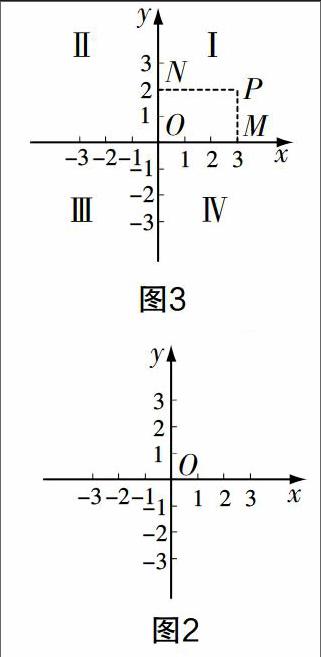
接着模仿刚才用有序数对表示派出所、唯信网吧位置的方法（老师在屏幕上演示，如图3），在平面直角坐标系中画点P，从点P向x轴作垂线，垂足为M，点M对应的数是多少？从点P向y轴作垂线，垂足为N，点N对应的数多少？

点M在x轴上对应的数字3称为点P 的横坐标，点N在y轴上对应的数字2称为点P 的纵坐标，依次写出点P的横坐标和纵坐标，中间用逗号隔开，用括号括起来，得到一对有序实数对（3，2），称为点P的坐标. 这时点P可记作P（3，2）.

问题1：如果点P不在老师画的位置，而是在平面直角坐标系中的任何一个地方，你们能通过画图写出它的坐标吗？接下来请大家动手在自己刚才画的直角坐标系中任意画一点P，并通过画图写出它的坐标，画好后小组交流讨论.

老师巡视指点，并把有错误的选择几张投影，让大家共同分析错在哪里，最后每个小组选出一张做得最好的在班里进行成果展示.

归纳总结：在平面直角坐标系中任何一点都能写出它的坐标，点的坐标通常与表示该点的大写字母写在一起，注意“先横后纵”，用逗号隔开，加上括号.

问题2：一个点的坐标有多个吗？

引导学生一起探究得到：过一点有且只有一条直线与已知直线垂直，所以点的横纵坐标都是唯一确定的，一个点的坐标只有一个.

活动：出示带网格的平面直角坐标系，老师指出点的位置，让学生抢答点的坐标.

设计意图 先模仿用有序数对表示派出所、唯信网吧位置的方法，老师在屏幕上演示点的坐标的画法和写法，由刚才的实际问题抽象成数学问题，从特殊到一般，使学生感受到数学模型思想，归纳思想. 让学生在自己所画的平面直角坐标系中由点找坐标，写出点的坐标，然后小组交流讨论，老师巡视指点. 有的同学可能会把点画在坐标轴上，只要按上面的画图方法一样能得出它的坐标，让学生经过讨论或老师指点后解决. 有的学生在这个过程中可能把坐标顺序写反了，有的可能没有写括号，而这些生成都是我们所需要的，是宝贵的教学资源，能使学生深刻认识坐标的内涵. 最后引导学生探讨点的坐标的唯一性，在带网格的平面直角坐标系抢答点的坐标活动，使学生更深刻认识点的坐标.

2. 由坐标找点

问题1：在平面直角坐标系中知道任何一点都能写出它的坐标，那知道坐标能找到对应的点吗？怎么找？如坐标为（3，2）的点P该如何找？

有了刚才的经验，在老师的引导下，学生经过讨论就会很快找到方法.

总结：（老师板演讲解）先过x轴上表示3的点作垂线，再过y轴上表示2的点作垂线，两垂线的交点就是坐标为（3，2）的P點.

活动：请大家在自己画的平面直角坐标系中分别描出坐标是（2，3），（-2，3），（3，-2）的点Q ，S，R，然后小组交流讨论.

老师巡视指点，并把有错误的选择几张投影，让大家共同分析错在哪里，最后每个小组选出一张做得最好的在班里进行成果展示.

问题2：P（3，2）与Q（2，3）是同一点吗？S（-2，3）与R（3，-2）是同一点吗？

引导学生讨论回答：P（3，2）与Q（2，3）不是同一点，P（3，2）是过x轴上表示3的点的垂线与过y轴上表示2的点的垂线的交点，而Q（2，3）是过x轴上表示2的点的垂线与过y轴上表示3的点的垂线的交点；同理S（-2，3）与R（3，-2）也不是同一点（如图4）.

归纳总结：点的横纵坐标不能颠倒，点的坐标是有序数对.

问题3：一个坐标能对应多个点吗？

经过刚才的探究，学生交流讨论后能很快得到答案，老师对学生的回答进行综合总结：过横坐标的垂线与过纵坐标的垂线相交，由于它们只有一个交点，所以一个坐标只能对应一个点，由刚才的探究可知，平面上的一个点只能对应一个坐标.

引导学生总结：以前学过，数轴上的点与实数一一对应，今天我们经过探究发现：坐标平面内的点与坐标是一一对应的.

设计意图 经过由点写出坐标的探究活动，特别是在带网格的平面直角坐标系抢答点的坐标活动，学生不但深刻地认识了点与坐标的对应关系，还把点与坐标的思维探究活动推向了高潮. 老师趁热打铁，引导学生反过来探究由坐标找点，符合辩证的思维训练特点，能很好地培养发展学生的探究能力. 由于经过前面由点写出坐标的探究活动，这次的探究就会显得驾轻就熟，经过动手画图、讨论、交流展示，学生能够很轻松地理解坐标的有序性、唯一性，总结出坐标平面内的点与坐标是一一对应的，完成了数形结合从一维到二维的飞跃.

陶行知先生说，“发明千千万，起点一个问”，老师如何设计问题启发学生也是相同的道理. 课堂提问是数学教学的核心，是贯穿整节课的纽带，数学老师只有深入研究教材、研究学生，才能针对学生的实际情况，在合适的时机提出合适的问题，从而激发学生的学习兴趣、引发学生积极思考，达到少教多学、自主高效的教学效果.