增加成功体验，让学生的认知走向深入

吴静

[摘 要] 学生参与思维活动的积极性是思维习惯养成、思维深度延伸的第一保障. 如何彰显教师的专业智慧，启发学生的参与思维，是常态教学行为中需要高度重视的.

[关键词] 思维；体验；渐进；策略；初中数学；课堂

《义务教育数学课程标准》（2011版）明确指出，要加强学生在课堂的活动量，让他们体验作为课堂主人的快乐. 2016年中国学生核心素养发展纲要中，将“学会学习”“实践创新”作为六大要素中的两大要素. 由此可见，学生在学习过程中的参与度和深入度是教学策略中必须重点关注的一个环节，也是基于学生核心素养渐进塑造的关键所在.

笔者结合课堂实践，重在实践与研究学生在参与课堂活动中思维的深入和兴趣的倍增，以此促进学生思维效果的达成，渐进促使学生核心素养的提升. 结合教学实例，想方设法地让学生满怀信心地投入课堂教学中，利用学生的成功意愿，使学生能够对教学产生信心. 抓住学生年龄中获取成功体验的兴奋度和求知欲，将学生的兴趣和思维渐进引入关键的活动之中，循序渐进、由浅入深.

合作中体验成功，激活学习内

驱力

学生的兴趣分为两种，一种是由外而内的，这种是基于学生的表象兴趣而渐渐深入的，这种兴趣表现出的缺点是持续时间短暂，思维肤浅，而另一种是由内而外的，这种兴趣是由学生的内在学习需求萌发的，这种兴趣的动力强劲，持续时间长，学生在这种兴趣的促动下形成了强大的内驱力，是学习不断深入的原动力. 而这种内驱力的激活，需要教师善于利用教材中有价值的知识进行创设. 比如课堂活动中的合作学习，这种学习是基于共性问题的建构与解决生成的，合作的过程中，每个学生都会讲自己在问题探究过程中的想法，并进行彼此交流和补充，最终达成问题的共同达成. 参与合作的小组成员会为了小组的任务完成而努力，也会为了问题的解决而喜出望外，共同分享这份成功的喜悦. 而教师就要为学生创设这种合作的机会和空间，让学生通过合作探究获取知识. 这样不仅可以增加学生的沟通机会，还可以启发学生积极主动地向他人学习，开拓自身的思维，从别人那里吸取有价值的知识，同时还能把自己的观点讲述给他人，善于表现自己、展示自我，让学生在合作中收获知识与技能、分享成功与快乐、获取成长与突破.

笔者在教学“解直角三角形及其应用”的过程中，就为学生创设了一个合作实践的活动：让学生利用所学的知识与已有的工具去测量旗杆的高度. 为学生提供合作探究的机会，能让学生在深入的合作实践中分享成功的硕果，体验成功的喜悦，增加学习数学知识的信心和动力，激活学生参与数学实践与探究的内驱力. 在本节课之前，教师让学生准备一些用来模拟旗杆的物体，课堂教学时，让学生拿出自己带来的模拟物体，分组进行实验，进行实际测量. 教师并没有为学生制定实验的具体步骤，而是要求每个小组通过讨论、探究、实践，寻找本小组的具体实验方法. 在进行实践活动的过程中，小组的每个成员都积极加入实验方案的制定讨论中，课堂气氛一度很活跃. 通过一段时间的讨论、交流，各小组都给出了自己的测量方法，有的小组利用三角形相似，有的小组利用直角三角形的边角关系……通过这个教学实践活动，学生不仅得到了测量物体的方法，还在实际中运用了数学知识. 在实践活动的过程中，合作、探究让学生体验到了成功的乐趣，最终测量出了旗杆的高度，也让学生获得了成就感.

创设合作探究的实践活动，能让学生在合作、探究中不断地积累知识，在学习中吸取别人的长处、摒弃自己的缺点，让自己的思维更加完善. 在合作探究的过程中，能让学生有成功体验，能让学生对数学学习产生兴趣，从而激发学生的学习积极性.

竞争中体验成功，拓展思维深度

在大数据的当下社会，整个社会的竞争非常激烈，而且竞争无处不在. 面对这种现状，学生作为时代的接班人，就要从小具备竞争意识，并在竞争意识的渗透下慢慢深入实践学习，提升创新意识，有效促进实践创新能力的渐进提升. 在数学教学过程中，教師要改变以往的教学方法，多给学生提供参加教学活动的机会. 教师可以利用一些题目让学生进行讲解，采用竞争的方式，让学生把自认为正确的结论或巧妙的解答方法展示给其他人，以作示范，这样能让学生在讲解的过程中收获成功的体验，促进认知的深入.

教“绝对值”一课时，笔者就向学生提出问题：“你清楚x的绝对值是多少吗？”这时有位学生不假思索地说：“是x”. 教师没有对回答做正误断定，下面的学生就有些不知所措了，过会儿就开始就学生小声讨论. 一会儿，学生a说：“我不认同他的观点，我觉得x的绝对值也有可能是0. ”教师这时发话：“你能为你的想法说明理由吗？”学生a接着说：“因为你给出的x是一个字母，不是具体的数值，它不仅能是正数，还能是0，所以就能等于0了. ”这时学生b提出问题：“x能看成负数吗？”学生a：“可以的. ”学生c：“如果x是负数的话，那么x的绝对值要等于多少？”学生d：“还是x啊. ”学生e：“不是的，应该等于x的相反数. ”教师插话：“原因呢？”学生e：“绝对值都是正数，所以负数的绝对值就应当是其相反数，也就是-x. ”学生f面露疑惑：“绝对值可以用来表示距离，那么，距离也能是负的. ”教师插话：“距离怎么可能是负的？谁能给解释一下？”学生e立刻站起来：“x是负数的话，-x就是正数了. ”学生g：“如果x=-4，则有-x=-（-4）=4，因此-x就是正数. ”学生f仍疑问：“-x带的‘-是怎么回事？”学生g：“-x带‘-也不一定就表示负数，你看-（-4）就是正数. ”（这时别的同学开始点头认可学生g的观点，学生g露出了成功的笑脸）在大家的思维碰撞中，学生最终找到了x绝对值的三种情况.

课堂通过问题竞争回答的方式，使得学生积极参与、动脑思考，提高了学生的学习热情. 对问题的竞争回答，能让学生的学习好胜心得到满足，同时能鼓励大家积极发言，表达自己的见解，得到成功的体验，使知识的内涵更加深入.

探究中体验成功，深化知识理解

核心素养中“学会学习”“实践创新”两大素养从教育目的和实施策略中要求我们教师在教学的过程中要把学生放在首位. 而学生毕竟是学生，要让学生成为课堂名副其实的主人，关键在于教师主导价值的达成. 在课堂教学过程中，教师要让学生清楚自己在课堂被重视的地位，这样学生就会注意力集中，思维就会很活跃，求知欲就会很旺盛，他们会积极主动地投入课堂教学中，敢于把自己的质疑表达出来，从而主动寻找答案，得到成功的体验，提高认知水平.

如教学“乘方”一课时，学生对于幂运算中的指数运算总是出错. 教师看到这种情况，就有针对性地把学生的错误进行改编，变成判断正误，摆在黑板上，让学生一起来判断正确与否，如果是错误的，给予改正. ①x2+x3=x5；②x2×x3=x6；③（x2）3=x5；④x10÷x2=x5；⑤x7÷x3×x4=1；⑥x7×x÷x7×x=1. 学生的情绪一下子就被带动了起来，大家都很认真地看教师在黑板上写出的题目，并对其正确与否做出判断. 对于错误的题目，还给出了比较详细的分析说明，其他学生也能认真地听取同学的分析，还主动对本节课的知识进行了类比，帮助归纳和记忆，使学生对幂指数的运算掌握得更加深入.

运用错误问题也能让学生得到成就感，同时还能提高学生的辨析能力，促使学生主动参与，在积极情绪下使知识被深化，从而提高课堂教学效率.

在碰撞中分享成功，促进思维

生长

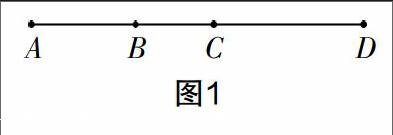
学生之间的思维或多或少存在着差异，学生的思维成果也有所差异. 在初中数学教学过程中，这种差异也越来越明显，而这种差异的存在不能成为学生智力生长的绊脚石，而应该成为学生思维增长的原动力. 如果教师巧妙用好学生思维差异的成果，让学生通过思维的碰撞和摩擦，巧妙导出各自的思维成果，就能让学生在思维的碰撞和摩擦中加深各自的思维深度和广度，达成学生思维能力的提升和生长. 而教师需要做的是，将学生课堂中思维碰撞的时间和空间还给学生，给学生思维留白的余地，给学生交流留白的余地. 比如，在“直线、射线、线段”的教学设计过程中，在课堂的最后一个环节，教师设计了如下问题：已知线段AD上有两点B，C（如图1），则图中有几条线段？

思考：在某次聚会中，A，B，C，D四個好友走到了一起，若每两人握手一次，则一共要握手多少次？

（教师出示问题，并留给学生一定的独立思考的时空，学生二至三人上讲台口述解题思路，供其他同学评议）

通过让学生“数线段”的活动，引导学生思考不同的方法，以拓宽学生的思路. 这样不仅能让上来展示的同学通过自己的语言表述自己的思维成果，还能让其他学生用心、用脑聆听别人的思维成果，在聆听和思考的过程中会发生无形的思维融合与摩擦. 当对其他同学的思维成果有异议时，还会发生新的思维碰撞和摩擦，彼此发生思维的进一步推进、深入，从而达成思维的再融合、观点的再交融，最终不仅将思维和方法提升到最大化，还在思维碰撞的过程中建构成学生自己知识基础上的方法构建. 就本题而言，学生通过“握手”实际问题回归到“数线段”的数学问题上，能在无形的思维中培养学生建立数学模型的能力.

总之，教师要给学生创设一个平等、民主的课堂，让学生大胆表达自己，使初中数学课堂教学的效果得到提高. 另外，教师要利用学生的成功意愿，给学生增加成功体验，从而让学生的知识认知走向深入.