初中数学生成性课堂的几点思考

杜晓霞

[摘 要] 学习的过程不是灌输，而应该是生成，初中数学教师在课堂教学中应该积极构建生成性课堂，唯有如此，才能有效提升课堂效率和学生的思维品质.

[关键词] 初中数学；生成性课堂；构建策略

初中数学教师在课堂上积极发掘生成性资源，因势利导构建生成性课堂，这将有效提升学生的能力发展，有助于课堂效率的提高. 本文首先分析生成性课堂的理论基础，然后结合教学实践对初中数学生成性课堂的构建策略进行探讨.

初中数学生成性课堂的理论

基础

1. 后现代课程观理论

1993年美国学者小威廉姆·多尔提出了“后现代课程观理论”，该理论强调对学生个人发展过程的关注. 对于课程，该理论不仅关注它的规划思路、设计理念、实施过程以及评价体系，也同样注重研究课程对人类形态、社会结构等方面的影响. 多尔充分吸收了皮亚杰、杜威等人的观点，创建出后现代主义的课程理论体系. 多尔认为，后现代主义的课程应该是建构性和非线性的，而不能是预先设定的. 该理论由多个领域的研究成果融合而成，因此本身就具有多元化，在这样的课程观指引下，学习不能存在统一的模式，因此课程的设计和创作应该与多元化匹配，而且要充分地将多元化和发散性融入课程设计. 所以我们的教学必须以学生为中心，要让学生积极参与到课程设计中.

初中数学课堂中，教师关注学生的思维发展以及灵感闪现，其实就是在发掘学生这一方面的课程因素. 充满教学智慧的教师由此进行灵活生成，这就是新型的初中数学课程的建构.

2. 生成性学习理论

生成性学习理论为生成性教学提供了直接的心理学依据. 该理论由美国学者维特罗克最早提出，他指出学习过程是学生的主动建构过程，该过程中，学生不应该是被动的接受者，而应该是主动的参与者，应主动建构自己的认知体系，并形成结论. 该理论还认为，学生可以不理解教师所提供的信息，但是一定要理解自我生成和加工的信息，认知的生成过程就是学生结合自己的知识基础，对新的信息进行选择、加工和接纳的过程.

在这一理论指引下，初中数学课堂应该关注学生的个体体验，尊重学生学习过程中的主体地位和认知规律，围绕学生的思维发展来搭建生成知识的平台.

初中数学生成性课堂的构建

策略

1. 放缓概念的引入过程，让概念自然生成

数学概念是数学知识大厦的脊梁，也是学生数学学习的基石，概念的引入过程急不得！概念是反映事物本质属性的思维形式，数学概念具有高度抽象的特点. 每一个数学概念在数学知识体系中都占有一定的地位，与其他概念之间存在着必然的联系，学生对数学概念的获得往往是通过自己的观察、感知、体验、抽象和概括等过程，将新的概念与已有认知结构中的相关概念建立联系，并将新的概念建构到自己的知识结构中. 因此，在概念教学中，要放缓概念的引入过程，揭示新概念与已有概念之间的联系，给予学生充分的时间去感知、体验和探究概念的生成过程，同时，概念的引入过程也是让学生自己抽象、概括新概念的过程，这样，能使学生感受到新概念的生成是一个自然流畅而又水到渠成的过程.

例如，笔者在和学生学习“平面直角坐标系”这一知识时，引入环节虽然用时不到3分钟，但是进程放缓，从学生熟悉的情境出发，帮助学生实现认知、经验和能力的有序发展，在这3分钟内，引入环节设计如下.

（1）复习旧知识：要求学生回忆数轴的相关知识，找到数轴上的点与实数之间存在的一一对应关系.

（2）联系生活情境：“影院的座位和一张电影票”，首先遮住座位号，只给学生看到“排”，提出问题：能不能根据这个信息找到自己的座位？如何才能确定座位？

通过这样的引入设计，学生在思考与交流的过程中对于“平面内的点与有序的实数一一对应”有了一定的概念，能将学生很顺利地带入课堂知识探究之中.

2. 展现概念的发展过程，让概念自然生长

每一个数学概念都有其一定的背景，概念的引入都有其合理性，因此，在概念教学过程中，要揭示概念之间的内在联系，展现概念的发展过程，让学生在已有概念的基础上亲身经历概念的生成过程和发展过程，这样，学生对概念的生成过程和發展过程才能做到清晰明了，也才能更好地体会概念的合理性，才有利于概念在学生的头脑中自然地生长.

例如“等腰三角形性质”的教学，笔者进行了如下设计，展现概念的发展过程，在师生互动的过程中促进概念的自然生长.

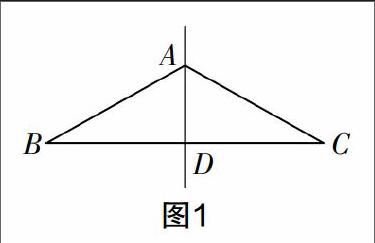
活动1 要求学生拿出预发的等腰三角形纸片，如图1，沿顶角对折后再展平，有什么发现？

学生通过观察后会有如下发现.

发现1：对折后，左、右两半图形能够重合.

发现2：等腰三角形是轴对称图形.

这两个发现显然是连为一体的，发现1是粗浅的现象发现，发现2相比较而言有一个思维抽象的过程. 待学生有了这样的发现和认识后，我们可以进一步提出问题和进行活动，促进学生的认知向前发展.

问题1：等腰三角形的对称轴是什么？

问题2：对折后，观察两个底角有什么关系.

活动2 现在请拿出笔画一画这个等腰三角形底边上的中线、高，以及这个等腰三角形的顶角平分线，看一看你有什么发现.

相比较发现1、发现2而言，要想让初中生全面地认清“等腰三角形的性质”，此时的进一步通过问题的引领和活动的编排可以促进知识在学生的头脑中不断地自然生长.

3. 揭示概念的本质内涵，让概念有序建构

概念的本质内涵是指反映在概念中的对象的本质属性，学生对概念本质内涵的把握也是一个缓慢有序的过程，建构概念的关键是在经历概念的生成过程和发展过程的基础上理解概念的本质内涵，搞清楚概念之间的内在联系. 因此，在概念教学过程中，要揭示概念的本质内涵，让学生清楚概念的来龙去脉，深刻理解概念的本质含义，促使学生将所学的概念融合到自己相应的知识结构中，与其他概念建立实质性的联系，并在概念体系中建构新概念. 这样，学生对概念的建构才是建立在已有概念基础上的意义建构，才是合理有序的建构，建构的概念在学生的头脑中才能持久而深刻，学生也才有可能运用概念提出新问题、解决新问题.

例如，笔者在和学生学习“解直角三角形”第二课时时，首先对这节课的教学要求进行了分析和研究：这节课的教学要求是什么？是以“解直角三角形”的经验、方法为基础，在此基础上“解非直角三角形”. 这节课对于初中数学教学有着承上启下的作用，所谓承上，即通过这节课的学习，学生对特殊锐角三角函数和解直角三角形这些数学概念的理解会更为深入；所谓启下，就是学生在这节课学习后，为后续的概念应用打下坚实的基础. 再结合所教班级学生的特点，在上课之前笔者思考了如下几点：（1）如何帮助学生有效复习特殊锐角三角函数值；（2）设置怎样的情境引导学生理解并学会添加辅助线.

有了上述思考，笔者在教学环节的设计上，采用了如下几个步骤，引导学生有序地构建数学概念.

环节1：（请基础较为薄弱的学生）回忆特殊锐角的三角函数值. （基础差的如果能够有效回忆出原有知识，那么其他同学也应该没有问题）

环节2：精选例题（例1为有一个特殊角的锐角三角形，已知一角和两边，要求学生求解另外一边和两角；例2为有一个特殊锐角的钝角三角形，已知两角和一边，求三角形的周长；例3在例2的基础上进行变式处理，其他不变，求三角形的面积），学生在解决例题的过程中，逐步接近数学概念的内涵与本质，在解决问题的过程中实现数学概念和方法的有序建构.

此外，我们的初中数学还应该强化概念的具体应用，引导学生感悟概念的应用价值. 任何一个数学概念都有其应用价值，学生不会应用概念解决问题，说明对概念本质的理解还停留在一知半解上，相应概念的知识体系还不完整. 因此，在概念教学过程中，要让学生感悟概念的具体应用，深刻体会概念的应用价值之所在，同时，概念应用也是促进学生完整建构概念，加深对概念本质理解之必须.