基于正交表的前纵梁拼焊板安全性设计∗

徐峰祥，田轩屹

(1.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉 430070；2.工程车辆轻量化与可靠性技术湖南省高校重点实验室，长沙 410114；3.武汉理工大学，汽车零部件技术湖北省协同创新中心，武汉 430070；4.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082)

基于正交表的前纵梁拼焊板安全性设计∗

徐峰祥1，2，3，田轩屹4

(1.武汉理工大学，现代汽车零部件技术湖北省重点实验室，武汉 430070；2.工程车辆轻量化与可靠性技术湖南省高校重点实验室，长沙 410114；3.武汉理工大学，汽车零部件技术湖北省协同创新中心，武汉 430070；4.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082)

提出了一种车身前纵梁帽形结构拼焊板的安全性设计方法。该方法拼焊板前纵梁的材料和厚度为离散变量，定义了考虑约束的目标特征函数。灵活运用正交试验设计，在迭代过程中并不断更新三水平正交表，进行拼焊板前纵梁离散变量的优化。设计过程中迭代调用有限元模型的次数明显减少，降低了计算成本并提高了计算效率，设计结果提升了拼焊板前纵梁的安全性能。与传统方法相比，该离散设计方法计算成本较低，且适用于多变量多水平的拼焊板结构设计。

前纵梁；拼焊板；安全性设计；正交表；多目标优化

前言

目前，汽车工业对车身轻量化的要求越来越高，需要充分利用材料组合的匹配来达到最合理的性能，这对设计者而言增加了设计的灵活性[1]。拼焊板技术在很大程度上能够达到上述的性能要求，可使材料等级和厚度属性等变量灵活匹配。

由于拼焊板结构的优势和良好的市场前景，促使国内外很多学者对拼焊板结构进行了轻量化设计的研究[2-6]；文献[7]中对代表前纵梁的S形梁从轻量化和耐撞性的双重目标进行了设计研究；文献[2]中利用近似模型对车门拼焊板内板的设计变量进行以刚度、自然频率和碰撞性能为目标的优化；文献[8]中采用响应面方法对拼焊板门内板进行优化设计。然而，对于像车身拼焊板结构耐撞性这类高度非线性的复杂工程问题，会导致近似模型的精度降低，难以保证优化结果的可靠性。虽然目前脱离近似模型的空间缩减技术能在一定程度上求解离散设计变量的优化问题，但缺少在局部设计区域内采样策略等[9]。

实际生产的高强度钢拼焊板的材料和厚度均为一系列离散值，而传统设计大多数针对连续设计变量进行研究。正交试验设计在求解离散设计变量和设计水平数较少的问题时非常有效，通过有限的计算次数就能寻得因素水平间的最佳匹配[10]。然而，随着离散设计变量和水平数的增多，常规正交试验设计方法需构造庞大的正交表，设计效率急剧降低，且不考虑约束，难以推广应用至车身拼焊板前纵梁耐撞性多目标优化设计。

本文中以汽车车身拼焊板前纵梁为应用对象，在传统正交试验设计方法的基础上进一步拓展和灵活运用，提出了一种针对离散变量特性的拼焊板前纵梁安全性设计方法。优化结果提升了拼焊板结构的安全性能，表明该设计方法能够应用于拼焊板前纵梁的耐撞性设计，具有一定的工程应用价值。

1 拼焊板前纵梁安全设计流程

具有离散变量特征的拼焊板前纵梁结构安全性设计是一个多因素多水平的多目标优化问题，若采用传统的正交试验设计，需要构造庞大的正交序列表，导致其计算效率非常低。本文中以传统正交试验设计方法为参考蓝本，提出了一种针对具有离散变量特征的拼焊板前纵梁安全性设计方法，其流程如图1所示。具体实施步骤如下。

步骤1：对不同离散变量组合的前纵梁拼焊板结构进行多参数分析，判定离散变量对拼焊板结构安全性能的影响，为优化设计的实施提供依据。

步骤2：建立离散优化问题，一般的离散优化问题的标准数学表达为

式中：F(x)为多目标函数向量；gj(x)和hk(x)分别为不等式约束函数和等式约束函数；M和Q为约束个数；x为设计变量向量；dij为设计变量i的第j个离散值；S为第e个设计变量的可选择值的数量；xL和xU分别为向量的下、上限值。

步骤3：建立三水平正交表。选择一个任意离散值并将其施加于第2个水平，设计变量的备选值在进行设计过程之前被确定。

步骤4：通过加权将多目标函数响应转化为一个与之等效的单目标函数响应，其特征函数为

式中：wi为第i个目标函数响应的权系数；fio(x)为第i个目标函数的标度值。

为了考虑约束条件，在原来的目标函数中加上一项罚函数，得到修正响应值，即特征函数[11]变为

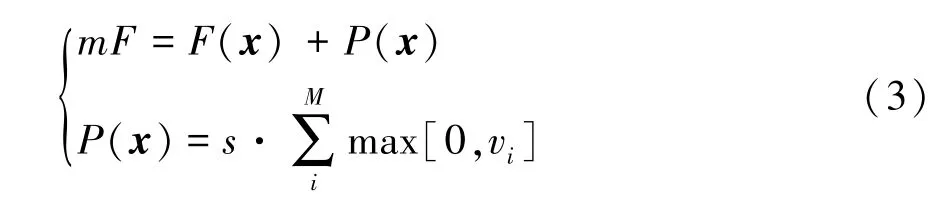
式中：P(x)为罚函数；vi为第i个约束函数的最大偏差程度；s为比例因子。

如果该设计问题有4个离散设计变量，分别为A，B，C和D，每个设计变量有3个水平，即该设计问题为四因素三水平。对正交表各样本点进行数值计算以得到各目标响应值，通过式(2)得到并评估正交表中每一行的特征函数值，注意此时的特征值是考虑带约束条件的函数值(式(3))，如表1所示。

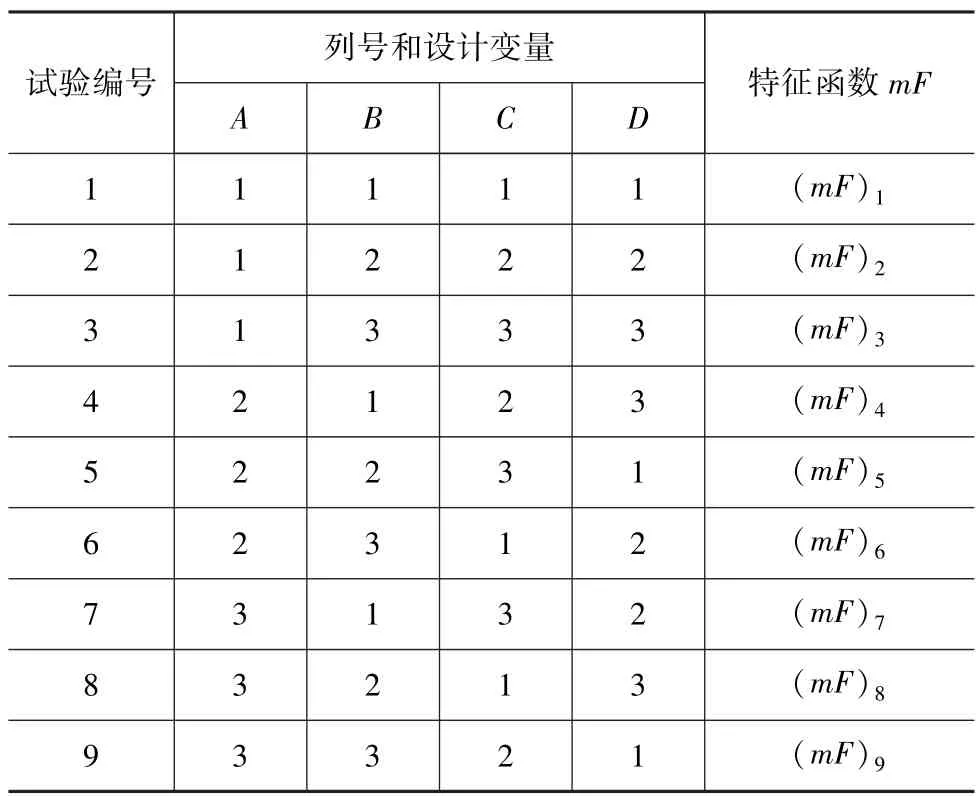
表1L9(34)正交序列表

步骤5：均值分析(见表2)。比较每个平均值，并选出平均值的极值，其所对应的设计变量的水平值被认为一个解。因为各因素间的交互作用被忽略，该解可能不是最优解，所以须将其对应的设计变量输入至数值模型做进一步的仿真计算，并将计算结果值与表1中的最小特征函数进行比较，选取两者中较小值所对应的水平作为当前迭代过程的最优解。

表2 计算对应每一水平的特征函数平均值

步骤6：收敛判定。条件为：连续5个最优设计的目标特征响应函数没有增大；或总的迭代次数达到最大(默认最大迭代数为2N，N为每个离散变量备选取值个数的最大值)。若满足终止条件则得到最终设计结果；否则转到步骤2继续进行。

2 车身拼焊板前纵梁安全性能描述

2.1 离散优化设计对象的抽离

本文中选取汽车车身前纵梁结构作为该离散迭代设计方法的典型工程应用对象(图2(a))，并将其进一步抽离为与之相类似的帽形拼焊板薄壁结构(图3(b))。该试件由不同材料或不同厚度的两段通过激光拼焊而成，焊缝位于轴向方向的中间位置，每段长200mm。帽形拼焊板的法兰盘部分和腹板部分通过40个焊点(每侧边分别有20个焊点)连接成一薄壁空腔整体，焊点间距为20mm，其详细几何尺寸参数描述见表3。

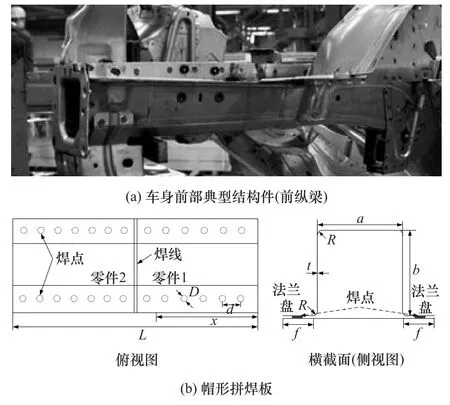
图2 车身前部典型结构件及拼焊板试件的几何描述

表3 帽形结构的几何尺寸参数mm

双相钢因其在延展性与高强度之间有着很好的平衡性而更适合于安全吸能结构[12]。此处所研究的拼焊板试样是由两种具有不同材料(DP590和DP780)和不同厚度(1.0和1.5mm)的双相钢通过激光焊接设备拼焊而成。

2.2 数值模型与验证

图3(a)是拼焊板结构台车动态碰撞测试装置，初速度为30km/h。采用非线性有限元软件LS-DYNA 971建立与该动态试验过程相对应的碰撞有限元模型，如图3(b)所示。通过Belytschko-Lin-Tsay缩减积分壳单元来离散拼焊板结构，该单元适合用于大变形分析，在厚度方向上有5个积分点，单元大小为5mm×5mm。整个台车被视为理想刚性体，质量为536kg，通过数值模型中一集中质量点来模拟。

图3 试验设备和碰撞系统模型

虽然壳单元和实体单元能在很大程度上提高仿真精度，但建模过程比较复杂，计算效率很低，且焊缝的宽度太窄，容易导致网格长宽比过大而造成计算不稳定等问题；焊缝区域的材料参数会随着母材的不同而有所差异，这势必会给焊缝处材料参数的求解带来不可估量的计算成本。因此，在对汽车车身拼焊板结构进行动态耐撞性仿真时，尤其是对于像高强度钢这种具有高应变率效应的材料而言，采用一般的共节点方法和刚性梁连接的焊缝建模方法所引起的误差是可以接受的。所以本文中忽略焊缝处的几何尺寸和材料属性等局部特性对拼焊板结构动态耐撞性的影响，仍然采用简单的共节点模型来连接焊接区域附近的母材壳单元。

图4示出了拼焊板结构动态试验与仿真的加速度时间历程，数值仿真结果与试验结果很好地吻合，可见建立的仿真模型能较好反映拼焊板结构在碰撞条件下的真实响应，可进一步用于后续的优化设计。

3 设计过程与结果分析

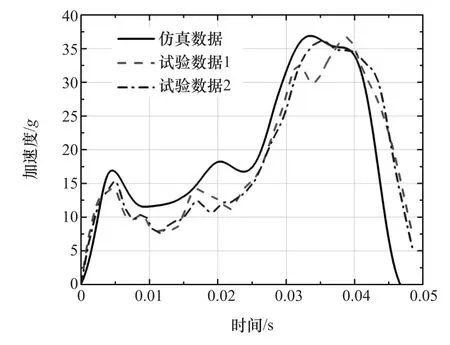
图4 拼焊板不同组合结构碰撞试验与数值结果对比

3.1 设计变量与评价函数

离散优化对象为前纵梁拼焊板组合结构，如图5所示，优化部件分为4个薄壁结构，不同部件的材料和厚度都是相互独立的离散值。设计变量共有8个，即4个部件的材料(a1～a4)和厚度(b1～b4)，每个部件有6种高强度钢等级和11种厚度属性可供选择(表4)。

图5 离散优化对象示意图

表4 离散设计变量和相应的取值

拼焊板结构的碰撞优化，本质是一个多目标优化问题，故在此将峰值载荷和质量的最小化作为优化目标，比吸能作为约束，则优化模型为

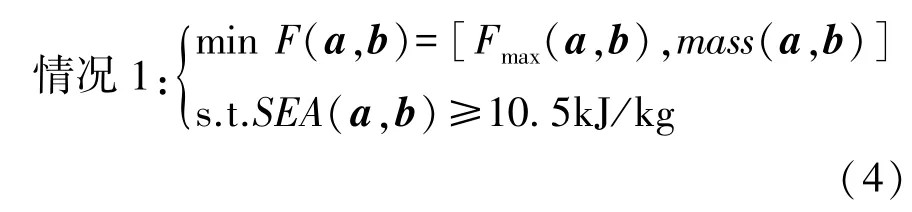
式中：a和b分别是材料类型和离散厚度向量(表4)。故该设计方法步骤4中的特征函数可以写为

式中：Fmax_0和mass0为原始设计的峰值载荷和质量；w1和w2分别为两个目标函数的权系数，作为特例，若其具有相同的重要性，则w1=w2=0.5。

在此考虑一种单目标离散优化，即吸能最大化作为优化目标，结构总质量作为约束条件，即

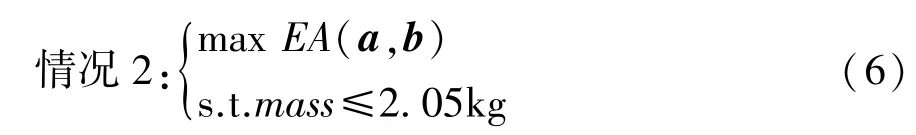
此时特征函数可写为mF=EA/EA0，其中EA0是在原始设计的总吸能。这样情况1和情况2都转化为以特征函数最大化为优化目标。

3.2 设计过程与结果

选择L27(313)正交表，根据该设计流程的步骤3建立三水平正交表并确定各离散设计变量相应的3个水平值。将初始设计的材料设定为a=(DP590，DP590，DP780，DP780)和厚度b=(1.5，1.5，1.5，1.5)，并将其施加于第2个水平，其余水平分别为其相邻的备选值。第1次迭代过程的变量设计水平见表5。

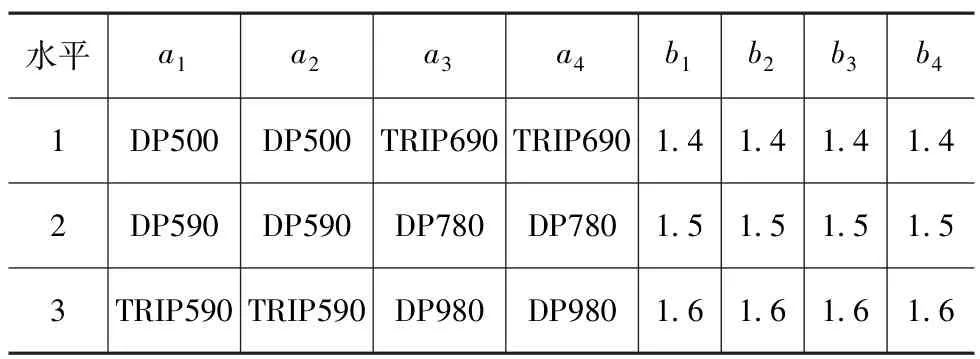
表5 第1个迭代步的设计变量水平

对表6中所列情况进行数值仿真，根据仿真计算结果，采用式(3)的罚函数法将约束附加至各个设计目标中，得到各设计目标的修正响应值。并由式(5)得到第1个迭代步各样本点的特征函数评分值，如表6中最右列所示。通过计算不同离散变量因素的3个水平所对应的特征函数值并取平均值，得到各因素的均值分析结果，见表7。

表6 第1个迭代步特征函数值

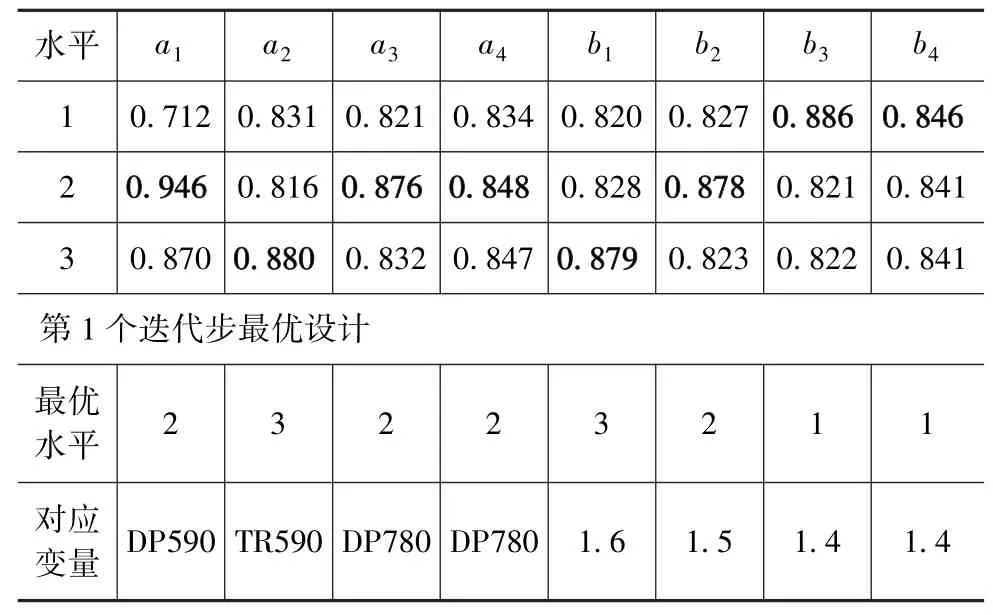
表7 均值分析计算结果及第1个迭代步最优设计

将设计变量输入至数值模型进行仿真计算，并与表6中各样本点所对应的目标特征函数值比较，两者选取最大值并将其所对应的水平组合作为该次迭代过程的最优设计(表7)。对高强度钢拼焊板耐撞性优化设计问题进行不断迭代，根据设计方法中步骤6的收敛条件，对于这两种情况，第9个和第6个迭代步的结果可以作为最后优化值，其离散优化迭代历程曲线如图6所示。

表8示出最后的优化结果和相应的设计变量。对于情况1来说，最优的峰值载荷和结构总质量比初始设计分别降低了49.2%和9.864%；对于情况2而言，总吸能增加到28.77kJ，增加幅度为27.58%。本文中所考虑的两种优化设计方案验证了所提方法的有效性。

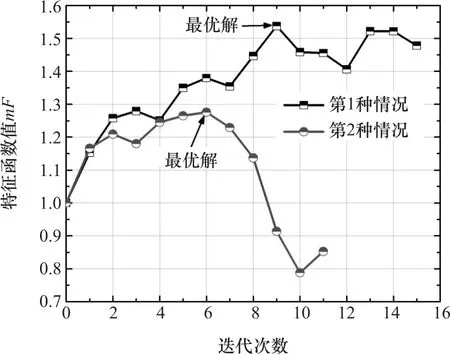
图6 两种离散优化情况的目标迭代过程

表8 两种优化情况的最后优化结果和相应的设计变量

4 结论

本文中研究了帽形高强度钢拼焊板薄壁结构的耐撞性问题，提出了一种基于三水平正交表的拼焊板前纵梁安全性设计方法，得到了以下结论：

(1)离散组合拼焊板的碰撞特性相差很大，材料和厚度等离散变量的合理匹配对拼焊板结构的碰撞特性有着直接且较大的影响；

(2)将组成拼焊板前纵梁的材料类型和厚度视为离散设计变量，定义考虑约束的特征函数，通过均值分析判定最新迭代的正交表；

(3)两种优化方案结果进一步提升了拼焊板结构的耐撞性，多目标优化结果，峰值载荷降低49.2%，结构总质量降低9.864%；单目标优化结果，总吸能增加了27.58%。

本文提出的设计步骤和流程更加简单，计算成本大大降低，计算效率较高，但得到的结果只是局部最优解，如何克服所提方法的不足并提高其精度有待今后进一步研究。

[1] 李淑慧，林忠钦，倪军，等.拼焊板在车身覆盖件冲压成形中的研究进展[J].机械工程学报，2002，38(2)：1-7.

[2] SONG S，PARK G.Multidisciplinary optimization of an automotive door with a tailored blank[J].Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，2006，220(2)：151-163.

[3] ZHU P，SHI Y，ZHANG K，et al.Optimum design of an automotive inner door panel with a tailor-welded blank structure[J].Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，2008，222(8)：1337-1348.

[4] PAN F，ZHU P，ZHANG Y.Metamodel-based lightweight design of B-pillar with TWB structure via support vector regression[J]. Computers＆Structures，2010，88(1)：36-44.

[5] 黄石华，成艾国，胡朝辉，等.基于6σ稳健性的拼焊板车门轻量化研究[J].汽车工程，2011，33(3)：262-266.

[6] 余海燕，高云凯，朱文峰.拼焊车门内板冲压成形性分析[J].汽车工程，2008，30(10)：923-926.

[7] HOSSEINI-TEHRANI P，NIKAHD M.Two materials S-frame representation for improving crashworthiness and lightening[J].Thin-Walled Structures，2006，44(4)：407-414.

[8] 胡朝辉，成艾国，王国春，等.多学科优化设计在拼焊板车门轻量化中的应用[J].中国机械工程，2010(4)：495-499.

[9] TANG L，WANG H，LI G Y，et al.Adaptive heuristic search algorithm for discrete variables based multi-objective optimization [J].Structural and Multidisciplinary Optimization，2013，48(4)：821-836.

[10] 白中浩，陈天志，曹立波，等.基于正交设计的汽车前纵梁吸能结构的优化[J].汽车工程，2010，32(11)：935-939.

[11] LEE K H，YI J W，PARK J S，et al.An optimization algorithm using orthogonal arrays in discrete design space for structures[J]. Finite Elements in Analysis and Design，2003，40(1)：121-135.

[12] PARUZ H，EDMONDS D.The strain hardening behaviour of dual-phase steel[J].Materials Science and Engineering：A，1989，117：67-74.

Safety Design of TWB Front Side Rail Based on Orthogonal Array

Xu Fengxiang1，2，3＆Tian Xuanyi4
1.Wuhan University of Technology，Hubei Key Laboratory of Advanced Technology of Automotive Components，Wuhan430070；2.Key Laboratory of Lightweight and Reliability Technology for Engineering Vehicle，College of Hunan Province，Changsha410114；3.Wuhan University of Technology，Hubei Collaborative Innovation Center for Automotive Components Technology，Wuhan430070；4.Hunan University，State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body，Changsha410082

A safety design method for tailor welded blank(TWB)front side rail with hat-shaped structures is proposed.With the method，the material and thickness of TWB front side rail are taken as discrete variables and the objective characteristic function is defined with consideration of constraints.By flexibly adopting orthogonal design of experiment and constantly updating three-level orthogonal array in iteration process，an optimization is conducted on the discrete variables of TWB front side rail.Obviously fewer runs of finite element analysis are needed in design iteration process，so the cost of calculation lowers，the efficiency of calculation rises，and the results of design enhance the safety performance of TWB front side rail.Compared with traditional method，the discrete design method proposed has lower calculation cost and suitable for the design of TWB structure with multiple variables.

front side rail；TWB；safety design；orthogonal array；multi-objective optimization

∗国家自然科学基金(51605353)、中国汽车产业创新发展联合基金(U1564202)、中央高校基本科研业务费专项资金(2016IVA037)、机械系统与振动国家重点实验室课题项目(MSV201608)和工程车辆轻量化与可靠性技术湖南省高校重点实验室开放基金(2016kfjj09)资助。

原稿收到日期为2015年6月15日，修改稿收到日期为2016年5月18日。

徐峰祥，博士，E-mail：xufx＠whut.edu.cn。

10.19562/j.chinasae.qcgc.2017.02.019