基于数据融合的电动汽车高压采集方法

邵仕平，黄菊花，曹 铭

(南昌大学机电工程学院，南昌 330031)

基于数据融合的电动汽车高压采集方法

邵仕平，黄菊花，曹 铭

(南昌大学机电工程学院，南昌 330031)

高电压采集是电动汽车电池管理系统的最主要任务之一。准确、稳定的高电压采集对电池管理系统估算SOC与SOH和动力电池安全管理等都有着重要意义。本文中提出了一种基于多传感器融合技术和卡尔曼滤波器的高电压采集方法。首先，对两种现有的高压采集方法进行了融合，解决了总电压采集数据的误差和噪声的问题；其次，对融合模型和卡尔曼滤波器进行了改进，精简了数据融合时的复杂计算；最后，通过实验证明所提出的高压采集方法具有较高的精度和稳定性。

电动汽车；高压采集；卡尔曼滤波器；数据融合

前言

随着能源危机和环境污染的日益加重，新能源汽车越来越受到重视，其中混合动力汽车、燃料电池汽车和纯电动汽车已有成熟的产品面世，而纯电动汽车更是因为其动力性强、经济性好、零排放等优点而被市场普遍接受。动力电池管理系统(battery management system，BMS)是电动汽车三大关键技术之一，其中采集动力电池组串联总电压是BMS的主要任务。总电压的采集精度直接影响BMS对电池组荷电状态(state of charge，SOC)和健康状况(state of health，SOH)的估算、电池组输出功率与绝缘电阻值的计算以及均衡策略，进而影响电动汽车整车性能与安全性。

由于串联电池组总电压一般在100～500V，所以AD转换器只能间接采集。目前采集电池组总电压的方法有4种：①分压法，该方法利用电阻分压的方式对总电压进行采样，但由于电阻精度和漂移问题，这种方法的采样精度较低，同时要求使用光电或V/ F(电压/脉冲)转换实现隔离[1-2]；②差分比例电路法，该方法通过差分比例电路对总电压进行线性缩小并采样，但如果电路元器件对称性较差，采样信号中会存在共模干扰，影响测量精度[3-4]；③电压传感器法，该方法采用霍尔式电压传感器对总电压进行采集，但由于霍尔电压传感器使用时需要通过采样电阻将电压信号转换为电流信号，这种采集回路存在漏电流，同时采样结果也受信号转换的精度限制；④单体电池电压累加法，该方法采集电池组全部单体电池电压，累加后得出电池组总电压。合理选择采集电路可减小单体电池电压数据的干扰，但该方法存在累加误差，且实时性较差。

此外，由于电动汽车工况复杂，采集电路会受到来自电机、DC/DC转换器等的外界干扰，所以仅使用上述方法在电动汽车平台无法获得良好的采集效果。为此，本文中基于多传感器融合技术和卡尔曼滤波器，设计了一种融合差分比例电路法与单体电池电压累加法的改进高压采集方法，对传统数据融合模型进行改进，精简了数据融合时的复杂计算，并将采集数据融合后的结果作为当前电池组总电压。最后通过实验验证了该方法的稳定性与采集精度。

1 硬件设计

1.1 概述

对于电动汽车BMS高压采集方法，差分比例电路法由于避免了使用隔离元器件和高精度传感器，相较于其他方法有成本优势。同时，监测动力电池组单体电池电压是BMS的基本功能[5-6]，所以单体电池电压累加法可在原有系统上实现，不需要修改硬件。因此对于融合二观测量的高压采集方法，选择差分比例电路法与单体电池电压累加法进行数据融合在硬件设计上是最优的。

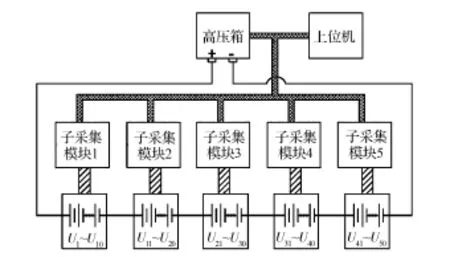
图1 分布式BMS结构示意图

本文中介绍的高压采集方法基于分布式BMS，管理45节100A·h磷酸铁锂串联电池组，基本结构如图1所示。该BMS采用Freescale公司DZ60作为MCU，具有12位ADC和CAN控制器，满足运算、采集和通信需求。BMS在高压箱内设有差分比例运算电路，其输入端直接与串联电池组正负极连接。BMS还具有5个子采集模块，每个子模块可采集10节单体电池电压，并通过CAN将数据发送至上位机。这样，BMS即可同时通过差分比例电路法与单体电池电压累加法采集串联电池组总电压。

1.2 差分比例运算电路法

差分比例运算电路法如图2所示。

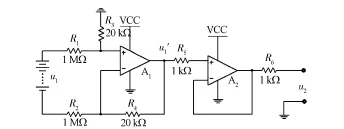
图2 差分比例运算电路法示意图

图2中u1为动力电池组串联总电压，A1和A2分别为OP279的两路放大器。R1～R4和A1构成差分比例运算电路，具体阻值参见图2。其中R1=R2，R3=R4，根据运算放大器的特性，此时放大器A1的输入电压u1与输出电压u1′的比值K=R1/R4。R5，R6和A2构成电压跟随器，增加电路跟随特性，不影响电压幅值，即u2=u1′。此时u1经过采集电路线性缩小为电压u2，并满足u1=Ku1′=Ku2。

通过DZ60单片机片内ADC采集u2，便可以计算出串联电池组总电压。其中，若电路内所有元器件为理想模型，则DZ60通过计算得出的串联电池组总电压u3与u1和u2的关系为

差分比例运算电路法由于元器件自身精度问题，无法实现完全对称，故采集时会存在较大共模干扰。但该方法误差小，电路直接测量电池组两端电压，可直观反映电压变化。

1.3 单体电池电压累加法

单体电池电压累加法如图3所示。

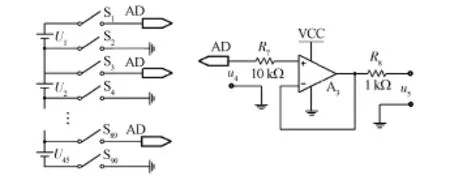
图3 单体电池累加法示意图

其中，U1～U45分别为电池组第1至第45节单体电池电压，R7，R8和A3组成电压跟随器，作为电压调理电路，S1～S90为开关阵列。当S1和S2闭合，其余开关断开，调理电路输入电压u4(1)等于U1，输出电压u5通过DZ60单片机片内ADC进行采集，此时u5(1)=U1。 闭合S3和S4，断开其余开关，此时u5(2)=U2。 通过循环控制开关阵列，即可测出U1～U45，累加后即可得出串联电池组总电压u6：

单体电池电压累加法的ADC与电池共地，所以采集时可忽略共模电压输入，但该方法存在较大的累加误差，造成总电压漂移。为减少误差，在实际应用中开关阵列采用光电继电器，可提高采集电路的一致性[7]，有助于进行误差补偿。

2 采集精度分析

2.1 离线测试

首先进行离线测试，通过高精度电源代替电池组，以修正两种采集方法因元器件性能问题造成的误差。对于差分比例运算电路法，由于R1～R4精度限制，会影响差分电路的对称性，因此K需要用补偿后比例值K′=48.11替代，以修正数据误差，结果如表1所示。

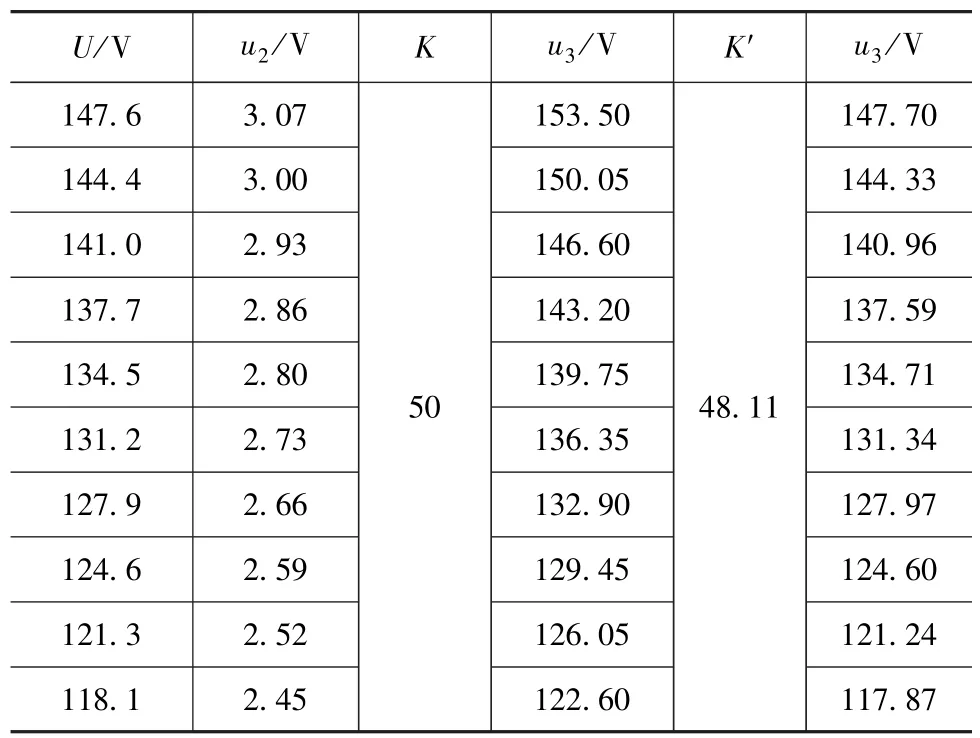
表1 差分比例运算电路法补偿测试

而对于单体电池电压累加法，由于电池数量较多，逐一补偿效率过低，没有实际意义。

2.2 静态测试

对两种采集方法进行静态测试，在开路情况下对电池组电压进行采集。断开电池组负载，静置3h，此时单体磷酸铁锂电池电压变化幅度小于2mV/10min，可认为串联电池组总电压U在短时间内恒定[8]，使用高精度万用表测量总电压U作为参考值，对比两种方法测量静态电压的精度。由于DZ60片内ADC精度为12位，所以转换结果保留3位有效数字。为消除随机误差，DZ60连续采集20次后取均方根，通过式(1)与式(2)计算出u3与u6，通过CAN发送至上位机，周期为500ms，取100次采集数据，结果如图4所示。

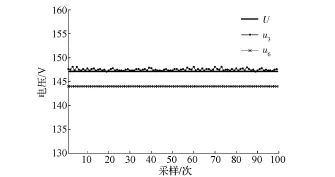
图4 静态电压采集对比

2.3 动态测试

为对比两种方法的动态电压的跟随情况，通过可编程负载对串联电池组恒阻放电1h，观察两种采集方法的精度。由于数据量过大，在全部7 200组采集数据中，在以30s为周期等距抽样出120组数据样本观察其采集精度，结果如图5所示。

图5 动态电压采集对比

2.4 测试结果分析

通过静态测试结果可以发现，差分比例运算电路法的数据含有较大噪声，但均方误差小。单体电池电压累加法相对误差高于2%，但该方法噪声小，在静态测量时信号十分稳定。

由图5可见，在电池放电过程中，由于差分比例运算电路法对总电压直接测量，无须累加计算，故电压采集的实时性更好，但存在噪声过大、数据不稳定的问题。单体电池电压累加法与静态采集时结果相似，噪声小但均方误差大。另外，无论静态还是动态测试，u6的1阶导数与U的1阶导数更为接近，即

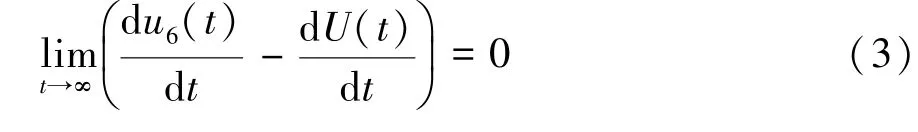
这说明在采集样本次数较多时，单体电池电压累加法更能反映电池组总电压的变化趋势。

3 数据融合模型

根据前面所述，由于差分比例运算电路法均方误差小，而单体电池电压累加法噪声低，故对上述两种方法采集到的总电压u3和u6作为系统的观测量进行数据融合，可以使高压采集结果获得更高的精度。

目前，常用的数据融合模型有：①最小二乘融合，该滤波模型包括平均值法、加权平均法等，其方差有下界，故无法保证融合结果的可靠性[9-10]；②序贯式融合[11-12]，该模型时效性较高，但在观测量之间存在较大差异时融合结果会产生较大波动；③扩维融合，该滤波模型采用多维滤波器，精度较高，但因存在多阶矩阵计算，会消耗过多的系统资源[13]，增加使用成本；④权值融合，该模型通过条件概率配置权值，使融合结果与输入量之间的差值达到最小，但对于二观测量融合模型，其输入过少，难以满足样本要求[14-15]。

针对上述融合模型的不足，本文中设计了一种基于卡尔曼滤波器的数据融合模型。当融合模型含有两个数据输入时，传统方法通常是使用两个卡尔曼滤波器对数据分别滤波后再对结果进行加权，或者通过对滤波器进行扩维或序贯处理。这样操作的原因是上述方法都认为在数据采集过程中，传感器数据只能作为观测量来使用。卡尔曼滤波器的状态更新方程和测量更新方程分别为

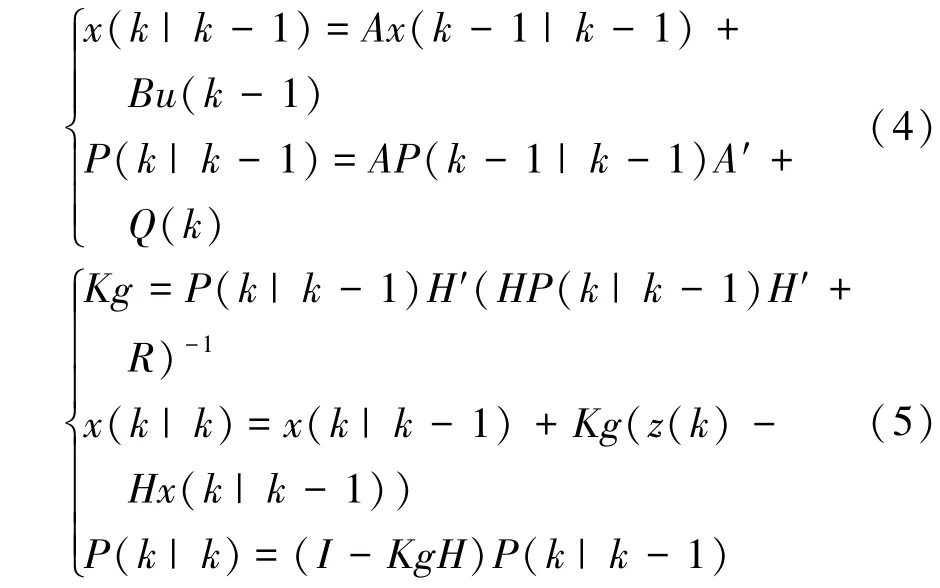
其中传统方法主要对式(5)中z(k)进行数据融合处理，如增加z(k)的维数，或者用多传感器测量值对z(k)进行序贯更新。同时在数据采集过程中，通常没有控制量，所以B=0，u(k)=0。然而在实际应用中，可使用一组传感器数据模拟控制量，作用到状态变量x(k｜k-1)。这样在数据融合时，可减少滤波器实际所需的观测量。对应于二观测量的融合模型中，实际滤波器所需迭代的观测量就减少为一个，实现一维卡尔曼滤波融合，这样就可减少滤波器的计算量，从而节约系统资源。

但需要注意的是，由于有一个观测量去模拟控制量，即该观察量实际并没有参与对测量方程的更新，而是直接用于状态方程，因此该观测量必须能准确反映被测对象的变化趋势，同时其测量噪声将作为过程激励噪声影响卡尔曼滤波器更新。因此在二观测量融合时，选择一个变化趋势接近被测对象，同时用噪声较小的观测量来模拟卡尔曼滤波器的控制量，才能达到本文中所设计的改进数据融合模型的最佳效果。参考图5和式(3)可以发现，单体电池电压累加法的结果u6完全符合上述条件。因此，只需对u6进行适当变化，使其转换为系统的“控制量”，即可完成滤波融合。

对于电动汽车BMS，其总电压U变化曲线是连续的，即U=U(t)。但在电池管理系统采集总电压时，由于单片机和AD转换器的采样限制，实际采集到的数据是离散的，对式(3)进行离散化，采用单体电池电压累加法所得到的总电压u6应满足：

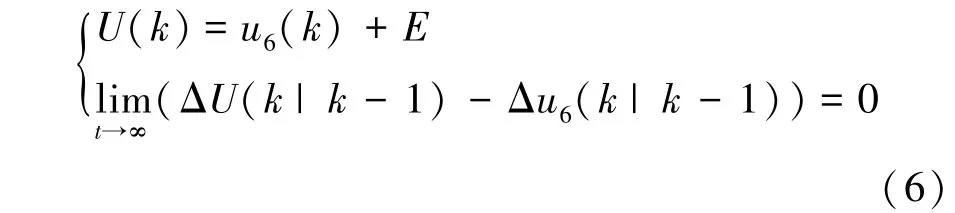
其中

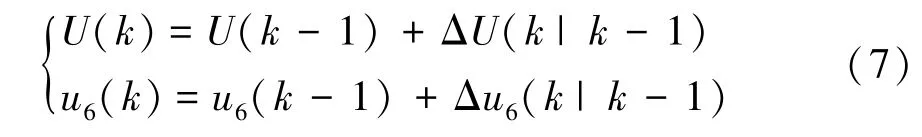
式中：U(k)为电池组实际总电压，k为采集次数。由于第k-1次采集时误差为E，由图4和图5可知，u6存在较大误差，无法直接使用，但在同一电池管理系统中，短时间内采集电路应具有相同的误差E，所以连续两次电压采集数据相减可以消除误差E。即过程模型可表示为

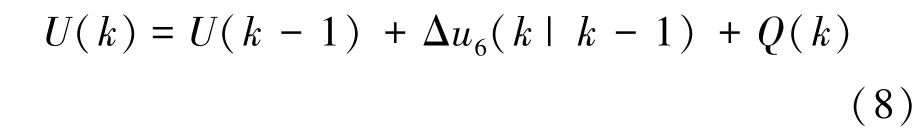
式中Δu6(k｜k-1)反映电池总电压的变化趋势，因此可以根据Δu6(k｜k-1)与U(k-1)预测当前的实际总电压U(k)，这样将单体电池电压累加法的结果u6从观测量转化为“控制量”，从而实现前面所述的对卡尔曼滤波器的降维处理；Q(k)为过程激励噪声协方差，可认为是单体电池电压累加法的测量噪声，参见图4和图5可知，Q(k)对结果影响较小，在系统资源紧张的情况下可以忽略。

卡尔曼滤波融合的测量模型参考差分比例运算电路法采集结果。同样，测量过程是离散的，采集结果u3直接反映总电压，因此测量模型可表示为

式中R为测量噪声协方差，参见图4，差分比例运算电路法噪声较大，R不可忽略。

根据上述状态模型与测量模型，即可进行状态与测量的迭代更新。将模型代入卡尔曼滤波器状态更新方程(4)与测量更新方程(5)，对于式(8)和式(9)中U(k)应用滤波器输出u7(k)替代。状态变量x(k｜k)为第k次融合的结果，即x(k｜k)= u7(k)。由于测量系统状态变量直接反映测试结果，所以系统参数A，B和H为1。控制量u(k-1)参考前面所述由u6进行转化，将式(8)代入式(4)可得u(k-1)=Δu6(k｜k-1)。观测变量z(k)= u3(k)。对状态更新方程与测量更新方程进行迭代，使x(k｜k)快速收敛至最小方差，这样数据融合后的结果u7(k)比u3(k)和u6(k)将更接近当前实际总电压U(k)。

通过上述滤波模型，可在系统存在两个观测量时，通过将单体电池电压累加法的结果转化为控制量，差分比例运算电路法的结果作为观测量，最终实现一维卡尔曼滤波器对两个观测量的融合。

4 仿真与测试

参照第2节的实验数据，对卡尔曼滤波融合模型进行性能仿真。首先，对实验数据分析可得静态测量噪声协方差R，同时忽略过程噪声Q(k)的影响。确定卡尔曼滤波融合模型参数后，使用第2节所述差分比例运算电路法与单体电池电压累加法测试结果u3与u6作为滤波模型的输入。在静态电压下，融合结果u7如图6所示。

对比图4可以发现，在静态测试中，滤波融合后的结果u7修正了u6的累加误差，并且在u3噪声较大的情况下，依然能快速收敛。图6中u7曲线几乎与实际总电压U重合，均方误差小于0.083%。

动态电压融合结果如图7所示。由图可见，动态测试中，u7同样能快速收敛至U，表现出对总电压良好的跟随性，并随迭代次数的增加不断修正采集误差。由于卡尔曼滤波器是通过迭代来减少均方差，所以收敛时间应该参考迭代次数。图7中u7在经过60次的迭代就已和U重合，缩短采集周期，可在短时间内达到较好的采集效果。

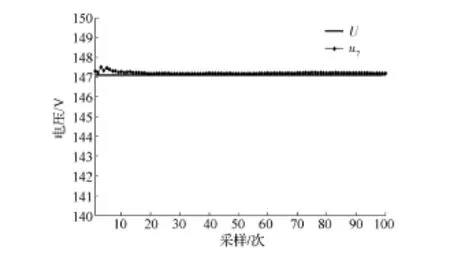
图6 静态电压融合

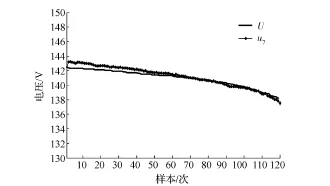
图7 动态电压融合

将第1节所述BMS移植到纯电动汽车实验平台上，如图8所示，以进一步验证本方法在动态充放电工况中的有效性。该平台是基于比亚迪F0改装的纯电动汽车实验平台。采用45节磷酸铁锂串联电池组，额定总电压144V，电机额定功率10kW。在该平台上进行1组动态充电工况实验和1组动态放电工况实验，每组实验前动力电池组均静置3h。

图8 纯电动汽车实验平台和直流稳定电源

第1组实验采用直流稳定电源以5A对动力电池组恒流充电1h，采集数据的处理方式与前面相同。实验结果如图9和图10所示。

第2组实验采用电机对动力电池组进行恒功率放电，放电时间为1h。实验结果如图11和图12所示。

上述2组动态充放电工况实验结果验证了本方法的融合结果u7均可以在较少的迭代次数下完成对U的收敛，而且采集数据的精度高于差分比例运算电路法的采集结果u3和单体电池电压累加法的采集结果u6。因此，本方法在不同工况下均具有较高的稳定性和精度。

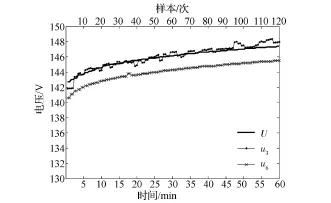
图9 动态充电工况电压采集对比

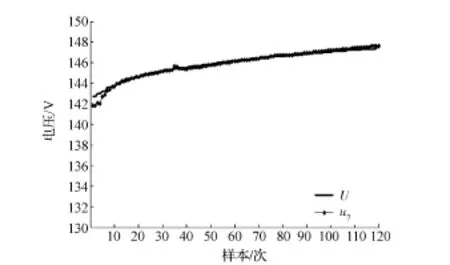
图10 动态充电工况电压融合结果

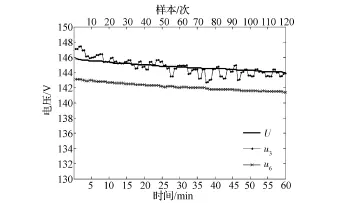
图11 动态放电工况电压采集对比

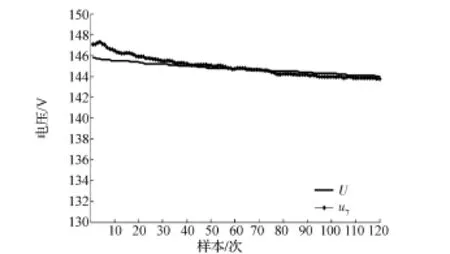
图12 动态放电工况电压融合结果

5 结论

本文中对电动汽车串联电池组高压采集方法进行研究，分析了现有采集方法的不足，提出了一种基于卡尔曼滤波器的新型高压采集方法。该采集方法改进了传统卡尔曼滤波状态模型与测量模型，将电池电压累加法作为系统的控制量，差分比例运算电路法作为观测量，在一维条件下实现上述两种采集方法的融合。实验结果表明，该采集方法结果比原有方法有更高的采集精度和信噪比，而比其他高精度高压采集方法有更低的成本和更高的稳定性，对提升电动汽车BMS性能具有重要的意义。

[1] 周晨.电动汽车BMS中高压检测系统的设计与实现[D].合肥：合肥工业大学，2013.

[2] 李树靖，林凌，李刚.串联电池组电池电压测量方法的研究[J].仪器仪表学报，2003，24(4)：212-215.

[3] 张彩萍，张承宁，李军求.电动车辆动力电池组电压采集电路设计[J].电气应用，2007，26(12)：91-93.

[4] 徐国金，吴健，温家鹏，等.基于误差分析的电池组高精度测量系统的设计[J].仪器仪表学报，2013，34(9)：1989-1996.

[5] 南金瑞，孙逢春，王建群.纯电动汽车电池管理系统的设计及应用[J].清华大学学报(自然科学版)，2007，47(S2)：1831-1834.

[6] 刘晓康，詹琼华，何葵，等.电动汽车用电池管理系统的研究[J].华中科技大学学报(自然科学版)，2007，35(8)：83-86.

[7] 蒋新华，雷娟，冯毅，等.串联电池组电压测量的新方法[J].仪器仪表学报，2007，28(4)：734-737.

[8] 李哲.纯电动汽车磷酸铁锂电池性能研究[D].北京：清华大学，2011.

[9] 岳元龙，左信，罗雄麟.提高测量可靠性的多传感器数据融合有偏估计方法[J].自动化学报，2014，40(9)：1843-1852.

[10] 牛胜锁，梁志瑞，张建华，等.基于广义岭估计的电力系统谐波状态估计[J].电力自动化设备，2012，32(7)：94-98.

[11] 马丽丽，张曼，陈金广.多传感器集中式增量卡尔曼滤波融合算法[J].计算机工程与应用，2014，50(11)：229-255.

[12] 冯肖亮，文成林，刘伟峰，等.基于多传感器的序贯式融合有限域H∞滤波方法[J].自动化学报，2013，39(9)：1523-1532.

[13] 余安喜，胡卫东，周文辉.多传感器量测融合算法的性能比较[J].国防科技大学学报，2003，25(6)：39-44.

[14] 任光，刘军，朱利民.并行多参考模型卡尔曼滤波系统仿真研究[J].系统仿真学报，2000，12(6)：660-663.

[15] 魏克新，陈峭岩.基于多模型自适应卡尔曼滤波器的电动汽车电池荷电状态估计[J].中国电机工程学报，2012，32(31)：19-26.

A High-voltage Collection Approach for Electric Vehicles Based on Data Fusion

Shao Shiping，Huang Juhua＆Cao Ming
School of Mechanical＆Electrical Engineering，Nanchang University，Nanchang330031

High voltage collection is one of the primary task of battery management system(BMS)in electric vehicle(EV).The accuracy and stability of high-voltage collection are of important significance for the estimation of SOC and SOH by BMS and the safety management of power batteries.In this paper，a high voltage collection method is proposed based on multi-sensor fusion and Kalman filter.Firstly，two existing approaches of high-voltage collection are fused to tackle the error and noise issues of total voltage data collection.Then fusion model and Kalman filter are modified and improved and the complex calculation in data fusion is simplified.Finally it is demonstrated by experiments that the high-voltage collection method proposed has higher accuracy and stability.

EV；high-voltage collection；Kalman filter；data fusion

原稿收到日期为2015年12月10日，修改稿收到日期为2016年3月7日。

曹铭，讲师，E-mail：172022712＠qq.com。

10.19562/j.chinasae.qcgc.2017.02.013