刚度、强度与频率约束下的白车身板厚尺寸优化∗

左文杰，陈继顺，李亦文，刘 念

(1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022； 2.汽车零部件先进制造技术教育部重点实验室(重庆理工大学)，重庆 400054； 3.大连理工大学工程力学系，大连 116023； 4.中国第一汽车股份有限公司技术中心，长春 130011)

刚度、强度与频率约束下的白车身板厚尺寸优化∗

左文杰1，2，陈继顺3，李亦文4，刘 念1

(1.吉林大学，汽车仿真与控制国家重点实验室，长春 130022； 2.汽车零部件先进制造技术教育部重点实验室(重庆理工大学)，重庆 400054； 3.大连理工大学工程力学系，大连 116023； 4.中国第一汽车股份有限公司技术中心，长春 130011)

全面地考虑了刚度、强度与频率约束，对某轿车的白车身结构进行轻量化设计。首先根据工艺要求对白车身结构进行了组件化建模，选取了关键的82个组件，每个组件中的板单元的厚度相同。其次在静态弯扭工况与自由模态工况下对车身结构进行了有限元分析。然后以质量最小为目标，以弯扭刚度、应力和前3阶固有频率为约束条件，板厚为设计变量，建立了白车身结构优化模型。最后采用序列线性规划进行非线性优化，取得了良好的轻量化效果：白车身质量减轻34.6kg，减轻率达11.4%。

白车身；刚度；强度；频率；结构优化；轻量化设计

前言

白车身结构的轻量化设计可以从结构、材料与工艺3个方面入手。如果从结构方面实施轻量化设计，其理论基础即为结构优化理论，也就是非线性优化理论与有限元分析的结合。文献[1]中提出结构优化理论后，迄今已经发展成熟。在航空工程领域得到了深入的应用，但是在汽车工程领域还有极大的应用余地，尤其是针对白车身这样的复杂结构。

目前有采用代理模型的方法对汽车零部件结构进行优化设计[2-3]。首先通过试验设计(正交试验、均匀试验等)对设计变量空间进行采样；然后对样本建立响应面模型(多项式响应面、Kriging等)代理原始的结构有限元模型；最后采用遗传算法或者粒子群算法等进化算法求解代理模型。代理模型法的缺点是模型精度低，除非采用大规模采样技术，但这造成了采样的计算量非常大。还有采用遗传算法、粒子群算法等进化算法直接对车身零部件结构的有限元模型进行优化[4-5]，放弃灵敏度信息的推导，造成计算量极大，以至于无法求解大型工程问题。

近年来也有采用基于梯度信息的优化方法，如准则法或者序列线性规划法，对车身结构进行优化设计。文献[6]中研究了轿车车身骨架在刚度约束下的轻量化设计。文献[7]～文献[10]中对客车骨架结构的静动刚度进行了灵敏度分析，对轿车骨架的断面几何形状进行了优化设计。

以上研究并未全面考虑刚度、强度和频率3类约束下的白车身结构优化。所以，本文中全面考虑这3类约束的要求，对白车身的板厚进行尺寸优化设计，实现轻量化目标。采用基于梯度信息的序列线性规划法求解该非线性结构优化问题。

1 白车身组件化设计

研究对象为某轿车白车身，共由161个钣金件构成，分为4个总成：侧围(side frame)、地板(floor)、车头(head)和车尾(tail)，如图1所示。图2～图6为这4个总成的爆炸视图。每个组件可包含多个钣金件，每个组件中的所有钣金件共享1个板厚设计变量。考虑对称性以及工艺的要求，本文中选取白车身82个核心组件，也即82个厚度尺寸设计变量。对图1所示的白车身结构划分有限元网格，板单元数约为24万，自由度总数约为152万。

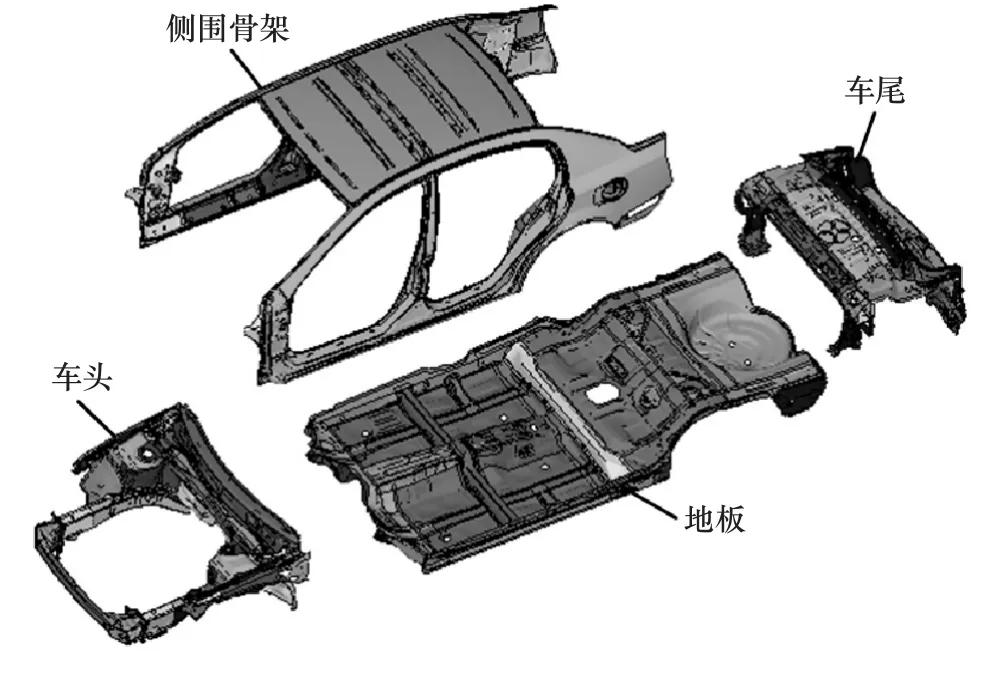
图1 白车身四大总成

图2 白车身侧围骨架组件

图3 白车身地板组件1

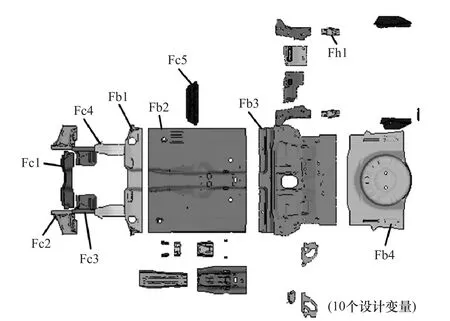
图4 白车身地板组件2

图5 白车身车头组件

图6 白车身车尾组件

2 响应定义

2.1 静态扭转工况

图7为扭转工况的载荷与约束示意图，即在左右前轮罩悬架弹簧支座支撑处施加大小相等、方向相反的铅垂力FT=5000N，并约束车身后悬架支撑点X，Y和Z向线自由度。

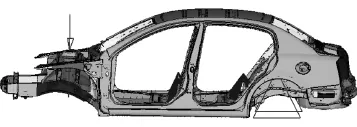
图7 扭转工况的载荷与约束

扭转刚度定义为

式中：MT为扭矩；Δφ为扭转角；B为轮距，B=1.0m；uT为悬架支座的铅垂方向与前纵梁交点的垂向位移。

式(1)是关于节点位移uT的函数。另外，还需要求解出该扭转工况下每个单元的应力其中e为单元编号。

2.2 静态弯曲工况

弯曲工况需约束后悬架支撑点Z向线自由度和前悬架固支撑点X，Y和Z向线自由度，并在前后座椅处施加模拟乘客质量的5个铅垂力其中1.6为安全系数。图8为弯曲工况的载荷与约束。

那么，弯曲刚度定义为

式中uB为门槛处的最大垂向位移。另外，还需要求解出该工况下每个单元的应力

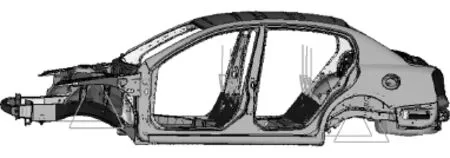
图8 弯曲工况的载荷与约束

2.3 模态工况

2.3.1 车身激振分析

行驶中车身受到的周期激励主要有路面不平整激励和发动机激励，车身结构的主要阶次固有频率应该避开激振频率。车轮不平衡激振，频率与车速有关，如车速控制在150km/h以内，频率在21Hz以下。

轿车在使用过程中，发动机的工作状态主要有两种：怠速状态和正常行驶状态。怠速状态即发动机空转耗油，车身制动未行驶的状态，转速范围为550～800r/min。轿车正常行驶状态下，发动机转速范围为1 500～3 500r/min。

发动机的振动激励频率为

式中：点火阶次为发动机一个完整周期内点火的次数。由于本文所研究的轿车使用的发动机类型为4缸4冲程汽油发动机，所以点火阶次等于2。将怠速转速范围与正常转速范围分别代入式(3)，得到发动机怠速状态和正常行驶状态激励频率范围为18.3～26.6Hz和50.0～116.7Hz。所以白车身前3阶固有频率一般应在27～45Hz之间。

2.3.2 车身模态分析

除去自由模态的前6阶刚体模态，对标车身第1阶固有频率为29.4Hz，不在两类激励频率范围内。本文中设置频率约束下限值为对标车身频率值，这样保证优化后前3阶频率仍不在激励频率范围内，同时动刚度也优于对标车身。

3 白车身尺寸优化

3.1 优化模型

建立白车身在以上3种工况下的优化模型为

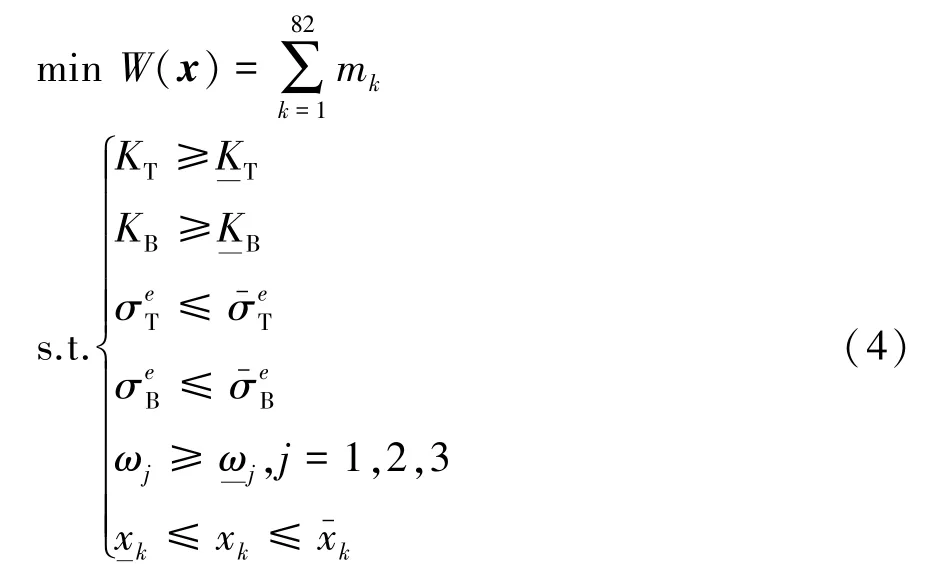
式中：mk和xk分别为第k个组件的质量和板厚设计变量；弯扭刚度与频率的约束下限值源于以上对标车身，其值分别为应力强度约束上限值为材料的屈服强度。

式(4)是高度非线性规划问题，一般采用序列线性规划求解，即将目标函数和约束函数线性近似展开，转化成线性规划问题。第l步迭代，将式(4)泰勒展开得到：

式中∇为梯度算子。单纯形法可求解式(5)的线性规划问题。此外，式(5)中需要提供弯扭刚度、应力以及频率关于设计变量的灵敏度，详细推导过程见文献[7]和文献[9]。由于该优化模型中，应力约束数量庞大，所以在优化中需要对应力进行筛选，选取接近约束边界的前20%的应力加入到优化模型中。当迭代过程中目标函数的改变量与初始目标函数之比小于0.3%时，满足收敛条件，终止迭代。

3.2 优化结果

在配置为Intel i7四核CPU、8G内存的笔记本电脑上求解，花费时间约10h，大部分时间花费于每一迭代步中的模态分析。经序列线性规划的26次迭代后满足收敛条件，得到最优解。目标函数车身质量变化曲线如图9所示。图10～图14显示了迭代过程中各响应的变化趋势。从图中可看出，最优解并未违反约束，优化得出的解是可行解。优化前后车身各部件厚度对比如图15所示，车身质量减轻34.6kg，减轻率为11.4%，最优解的弯扭刚度与对标车身持平，前3阶频率略有提升，弯扭工况下的应力也未超出屈服应力。

图9 白车身质量迭代过程

图10 扭转位移响应迭代过程

图11 弯曲位移响应迭代过程

4 结论

以车身质量最小化为目标，以弯扭刚度、弯扭强度以及前3阶固有频率为约束，以各组件板厚为设计变量，对白车身结构实施了轻量化设计。轻量化效果为：车身质量减轻34.6kg，减轻率为11.4%，最优解的弯扭刚度与对标车身持平，前3阶频率略有提升，弯扭工况下的应力也未超出屈服应力。相比于现有白车身刚度优化的研究成果，本文中的创新点是将应力强度约束也施加到优化模型中。传统的车身结构设计采用的是“刚度设计、强度校核”；本文实现了“刚度强度同时优化设计”。但没有考虑碰撞工况，下一步的工作拟通过基于梯度信息的等效静态载荷法将碰撞动态非线性优化转化为多工况静态优化进行求解。

图12 第1阶频率响应迭代过程

图13 第2阶频率响应迭代过程

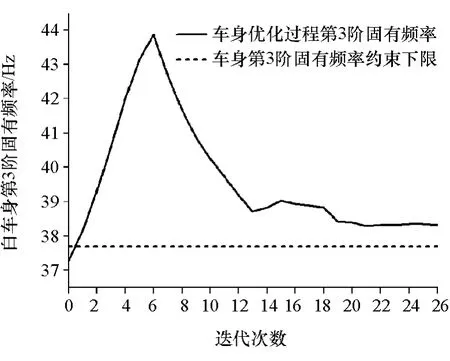
图14 第3阶频率响应迭代过程

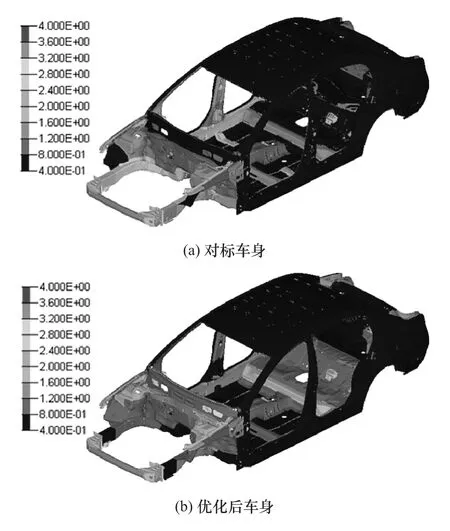
图15 优化前后车身板厚对比

[1] 钱令希.工程结构优化设计[M].北京：科学出版社，2011.

[2] 丁炜琦，田程，范子杰.基于代理模型的大客车结构动态特性多目标优化[J].汽车工程，2012，34(12)：1072-1075.

[3] 施颐，朱平，张宇，等.基于刚度与耐撞性要求的车身结构轻量化研究[J].汽车工程，2010，32(9)：757-762.

[4] 徐涛，左文杰，徐天爽，等.概念车身框架结构的多变量截面参数优化[J].汽车工程，2010，32(5)：394-398.

[5] 季枫，王登峰，陈书明，等.轿车白车身隐式全参数化建模与多目标轻量化优化[J].汽车工程，2014，36(2)：254-258.

[6] TORSTENFELT B，KLARBRINGA A.Conceptual optimal design of modular car product families using simultaneous size，shape and topology optimization[J].Finite Elements in Analysis＆Design，2007，43(14)：1050-1061.

[7] CHEN W，ZUO W，CHEN W，et al.Component sensitivity analysis of conceptual vehicle body for lightweight design under static and dynamic stiffness demands[J].International Journal of Vehicle Design，2014，66(2).

[8] ZUO W.An object-oriented graphics interface design and optimization software for cross-sectional shape of automobile body[J].Advances in Engineering Software，2013，64(5)：1-10.

[9] ZUO W.Bi-level optimization for the cross-sectional shape of a thin-walled car body frame with static stiffness and dynamic frequency stiffness constraints[J].Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering，2015，229(8)：1046-1059.

[10] 左文杰，白建涛，李亦文.考虑冲压工艺的前纵梁前端结构碰撞模型标定[J].汽车工程，2016，38(5)：561-566.

Size Optimization on Plate Thickness of BIW with Constraints of Stiffness，Strength and Frequency

Zuo Wenjie1，2，Chen Jishun3，Li Yiwen4＆Liu Nian1
1.Jilin University，State Key Laboratory of Automotive Simulation Control，Changchun130025； 2.Key Laboratory of Advanced Manufacture Technology for Automobile Parts(Chongqing University of Technology)，Ministry of Education，Chongqing400054；3.Department of Engineering Mechanics，Dalian University of Technology，Dalian116023；4.R＆D Center，China FAW Co.，Ltd.，Changchun130011

The lightweight design of the body-in-white(BIW)structure of a sedan is conducted with thorough considerations of stiffness，strength and frequency constraints.Firstly eighty-two key components are selected with the models for their BIW structure created，in which panels in the same component having same thickness. Then finite element analyses are conducted on car body structure under static bending，twisting and free-mode conditions，and an optimization model for BIW structure is set up with minimizing mass as objective，bending and torsional stiffness，stress and first three order frequencies as constraints and panel thickness as design variables.Finally sequential linear programming is adopted to perform a nonlinear optimization with a good lightweighting result obtained：the mass of BIW reduces by 34.6kg with a mass reduction rate of 11.4%achieved.

BIW；stiffness；strength；frequency；structural optimization；lightweight design

∗国家自然科学基金(51575226)、吉林省科技发展计划(20140101071JC)和汽车零部件先进制造技术教育部重点实验室开放课题(2014KLMT01)资助。

原稿收到日期为2015年9月1日，修改稿收到日期为2016年5月13日。

左文杰，副教授，E-mail：zuowenjie＠jlu.edu.cn。

10.19562/j.chinasae.qcgc.2017.02.005