好的例题教学是照亮学生解题的灯塔

臧 华

(安徽省池州市第八中学 247000)

提高课堂教学效果，充分发挥例题的作用，是减轻学生学业负担、把学生从题海战中解放出来的有效手段，已成不争的共识．笔者将通过一个例题的讲解，阐发自己的思考．

例已知函数f(x)=x3-ax2(a∈R)．若f(x)的切线过点(0,1) ，且它过点(0,1)的切线有2条，求实数a的值．

1 仔细审题是前提

读懂题目的条件和要求是正确解答的前提.本题给出了函数解析式(但含有参数a)、切线经过的点(0,1)、过点(0,1)的切线的条数，求参数a．

需要提醒学生注意的是对“f(x) 的切线过点(0,1)”的分析．将x=0,y=1 代入f(x)=x3-ax2，得1=0，不成立，可见，点(0,1)不在f(x)上．

对题目稍做变化，将函数改成f(x)=x3-x2+a(a∈R)，则不能断定点(0,1)是否在f(x)上．实际操作中，可能有的学生不假思索就把(0,1)当成f(x)上的点，将x=0,y=1代入f(x)=x3-x2+a，得a=1，从而使问题简单化，当然是错误的．想一想，这样就能得出结果，题目给出的条件“过点(0,1)的切线有2条”有什么用呢？

2 厘清思路好扬帆

由于是与切线相关的问题，而且是一元三次函数，学生立即想到用导数方法求切线斜率、进而求切线方程，再通过切线方程寻找求a的思路，是非常自然的．下面笔者顺着这一思路且讲且解．

因为点(0,1)在切线上，所以有

①

因为点(x0,y0)在f(x)=x3-ax2上，所以有

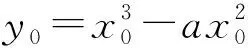
②

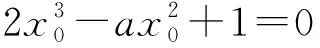
③

到此，可能有的学生不知道怎么进行下去了．可能有人会想，如果能直接求出x0就好了．事实上这是不容易的，因为方程中有两个未知量．不要因方程而迷失方向，我们要求的是a，至于x0是多少并非目标．怎么办？莫慌！还有一个条件未用．

由于过点(0,1)的切线的有2条，所以关于x0的方程③应有两个不同的实根．换句话说，若设g(x)=2x3-ax2+1，就是函数g(x) 的图像与x轴有两个交点．本来，如果g(x) 中不含参数a，则g(x)图像与x轴交点数是确定的，正因为有了含参数a，才导致g(x)图像与x轴交点数的不确定性．那么什么情况下图像与x轴有两个交点呢？这就要求我们研究g(x)图像的特征，特别是单调性和极值点．

设g(x)=2x3-ax2+1，

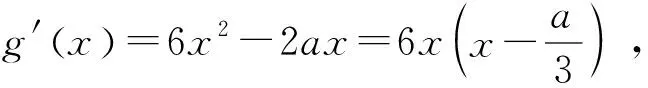
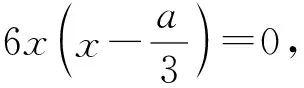
(1)当a>0时，

当x∈(-∞,0)时，g′(x)>0，g(x) 单调递增；

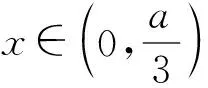
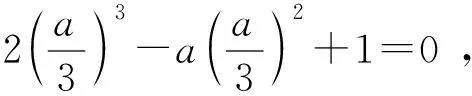
(2)当a=0 时，

曲线g(x)与x轴仅有一个交点，显然不合题意．

(3)当a<0 时，

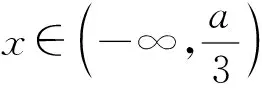
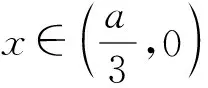
当x∈(0,+∞) 时，g′(x)>0，g(x) 单调递增.

综上可知，a=3．

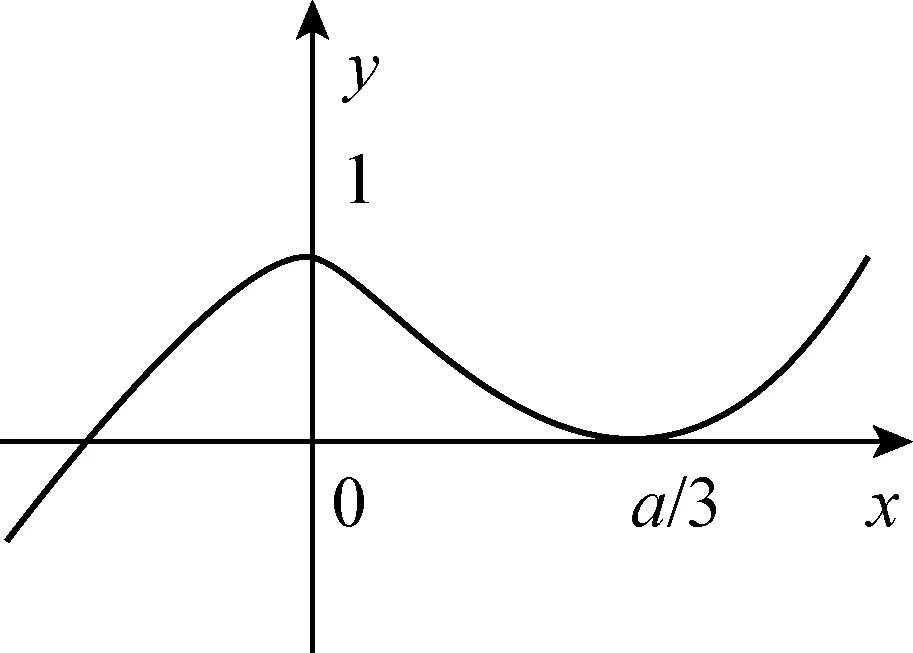
图1

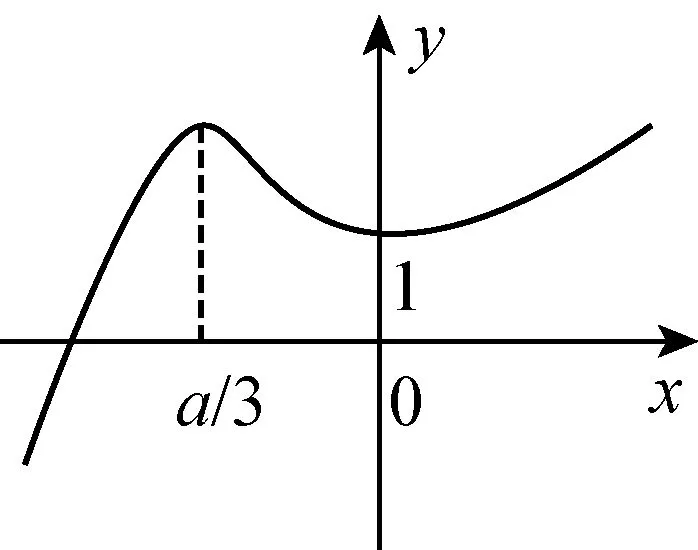
图2

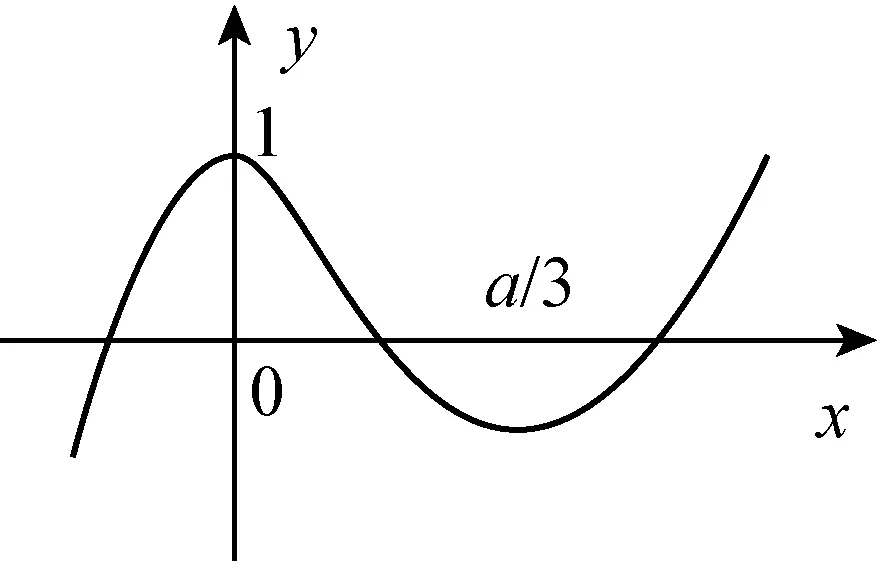
图3

3 一题多解思路活

设方程③左边多项式分解式为

2(x0-b)(x0-c)2，

展开整理得

比较方程③左边和上式得

a=4c+2b,c2+2bc=0 ，-2bc2=1 ，

联立上三个方程解得a=3．

这说明，解一道题可以灵活使用多种工具，不一定要一种方法走到底．

4 反思质疑求严密

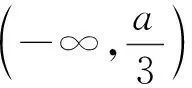
则g(-1)=-2-a+1=-1-a≤0；

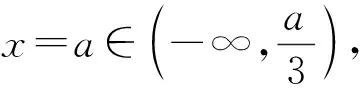
则g(a)=2a3-a3+1=a3+1<0．

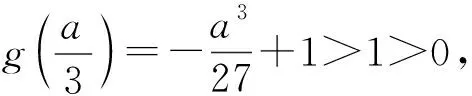
5 延伸拓展收获多

(1) 将“过点(0,1)的切线有2条”改为“过点(0,1)的切线有3条”．

当a=0 时，曲线g(x)与x轴仅有一个交点，不合题意．

当a<0 时，曲线g(x)与x轴仅有一个交点，不合题意．

综上可得a>3．

(2)将“过点(0,1)的切线有2条”改为“过点(0,1)的切线有1条”，结论又会怎样呢？

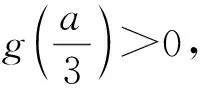
当a=0 时，曲线g(x)与x轴仅有一个交点．

当a<0 时，曲线g(x)与x轴仅有一个交点．

综上可得，a<3 ．

对于这一问，也可以直接分析得出.

曲线g(x)与x轴交点有四种可能：0个、1个、2个、3个.有2个、3个交点时，a的值已求出，分别为a=3、a>3．由于曲线g(x)与x轴至少有1个交点，即0个交点的情形不存在，所以曲线g(x)与x轴有1个交点时，a<3，即过点(0,1)的切线有1条时，a<3．

尊敬的读者，一题就讲了这么多，你是觉得啰嗦还是值得呢？笔者认为是值得的．如果我们贪多贪快，不把问题讲清讲透，“言及于数”，“不顾其安”，必然会使学生“隐其学而疾其师，苦其难而不知其益也”，“虽终其业，其去之必速”．作为学生，在老师讲过之后，还要经常复习、反复揣摩，温故而知新．倘若如此，例题的作用就会更大．