玩游戏学数学——一个八年级拓展性数学课程的实践

张安军

(浙江省台州市白云中学 318000)

2015年浙江省教育厅在《关于深化义务教育课程改革的指导意见》中指出，拓展性课程是指学校提供给学生自主选择的学习内容，明确要求，各地和学校要积极探索拓展课程的开发、实施、评价和共享机制，体现地域和学校特色，突出拓展性课程的兴趣性、活动性、层次性和选择性，满足学生的个性化学习需求，初中数学拓展性课程肩负着实现素质教育的责任和义务，是实现数学教学向数学教育转变的重要途径之一.笔者在本市组织的拓展性课程研讨会上，开设了八年级数学拓展课《玩游戏学数学》，现将本课的教学过程及教学点评撰写成文与各位同行研讨.

1 教学实录

1.1 体验游戏,激趣引入

师：这节课老师想和大家玩游戏，不过数学课中玩游戏，希望玩出数学味，在玩游戏[1](图1)之前，先熟悉其规则.

(学生阅读规则后，老师从反面提问，如图2，三支被吹灭的蜡烛，所选的是哪一支？又从正面追问，老师用椭圆的虚线选中一支蜡烛，将被吹灭的有几支？加深对游戏规则的理解.)

“吹蜡烛”游戏—18支 “吹蜡烛”游戏—18支

图1

图2

规则说明：

①甲、乙轮流任意选其中一支燃着的蜡烛，把它吹熄，同时所选的蜡烛及相邻的两旁都将被一起吹熄，每次轮流到只给一次吹的机会，②吹灭最后一支蜡烛者为胜。

师：同学们，你们认为该游戏的输赢和吹蜡烛的先后有关系吗？

(此时，教室里非常热闹，一部分同学认为游戏的输赢对先吹者有利，有的认为对后吹者有利，有的认为仅与博弈者的水平有关，还有的不清楚.老师前后邀请几位同学玩，这几位同学分别代表上述前三种观点，共玩了三局，在第一、三局中，先吹蜡烛者赢，在第二局中后吹蜡烛者赢.这时大家对输赢和吹蜡烛先后的关系更是议论纷纷.)

师：既然大家意见不一，那么我们就带着这个疑惑继续游戏探索之旅.

点评：以游戏为话题，点燃学生玩的欲望，为了更好玩游戏，老师引领学生解读游戏规则，边解读边提问为玩游戏作充分准备.当先吹者取胜时，后吹的挑战者又赢了先吹者，此时教师不失时机提出“游戏的输赢跟先吹或后吹有没有关系？”，会玩更要学会思考，要玩出数学味，把真实游戏情境、操作、体验融入一体，真正激起学生强烈认知冲突，点燃了学生探究的欲望.

1.2 合作交流，探究游戏

游戏2：有两行数量相等的扑克牌，甲、乙轮流在其中任意一行取扑克牌(每次取牌数量不限，但不能不取)，规定：谁取到最后一张牌者为胜.这个游戏的输赢和取牌的先后有关系吗？ 为什么？[2]

图3

(老师和学生一起解读游戏规则中的关键词并提出问题，如，你是怎样理解“任意一行取牌”？如果甲在第一行中取牌，那么乙能否再在第一行取牌？当所有学生全部理解游戏规则后，然后分组玩游戏，让学生在玩耍中验证自己的猜想.玩了4分钟左右，有的小组认为该游戏对先取牌者有利，有的认为对后取牌者有利，有的认为与博弈者的水平有关.)

师：大家对游戏的输赢与取牌的先后关系，意见不一，那么到底谁对呢？

生(众)：各自比试一下吧！

师：一开始时，我给每组分发20张，两行各10张扑克牌；现在我减少每行扑克牌的数量至8张，是否符合要求呢？

生(众)：符合要求.

师：那么每行还可以是几张？带着这样问题继续观看和思考几组的比试.

(老师让不同观点的同学比试，其它同学仔细观战；每局老师有意变化牌的数量，从多到少，随着局数的增多，后取牌者除了一次失误外，如图4，其余都赢.观看的同学慢慢地从中发现其中的奥秘.)

图4

师：刚才共观看三局，第一局每行8张，先取者赢；第二局每行5张，后取者赢；第三局每行3张，后取者赢.

师：如果第四局，每行都只有1张牌时，要想获得游戏胜利，你会选择先取还是后取？

生1:我会选择后取，因为先取者不管怎样取牌，总会留下1张牌给后取者.

师：当每行2张牌时，又如何呢？

生1：我还坚持后取，如果先取牌者在某一行中取1张，我在另一行也取1张，这时，两行都变成各1张，就转化为上述问题后取牌者有利；如果在某一行中取2张，我也取2张.总之，对后取牌者有利.

师：刚才第三局，每行3张牌，先取者取2张，后取者也取2张，这样转化为每行都只有1张牌，导致后取牌者赢；如果先取牌者取走1张，后取牌者应取几张，才能获胜.

生2：后取牌者也取1张.

师：为什么？

生2：当后取牌者也取1张时，就变成每行2张，由上述游戏解决知，后取牌者能赢.

师：两行数量分别为1、2、3张，这个游戏都对后取牌者有利，是否推广到任意数量相等的两行扑克牌呢？

生3：两行只要数量相等，这个游戏对后取者一定有利.

师：如图4所示，第一局每行8张，后取牌者为什么会输掉呢？

生3：是因为后取牌者失误了才输掉.

师：失误在哪一步呢？

生3：先取牌者第一次取了5张后，后取牌者应该取5张，而他因失误取了4张.

师：为什么后取牌者也要取5张.

生3：因为当后取牌者也取5张，这时两行都剩下3张牌，又转化每行都为3张牌.

师：刚才同学们很好地把数学中的化归思想迁移到游戏中来，对于两行任意数量相等的扑克牌，如果后取牌者要获胜，应如何取牌？

生4：后取牌者只要和先取牌者每次保持对称地取牌.

师：你这里所谓对称地取牌，是否指先取者在其中一行取牌，后取者一定要在另外一行相应的位置取相同数量的牌，也就是说后取者和先取者在形和数量上都要保持对称.

生4：是的.

师：还有不同的方法吗？

生5：后取牌者只要和先取牌者在另一行每次保持相等数量取牌，就可以，不必位置相同.

师：生5在生4的基础上，提出后取者和先取者只要保持数量相等就可以.其实游戏规则谁最后有牌取就赢，最终跟取牌的数量有关.因此生5把生4的想法推向更一般.

师：能否用数学的符号来描述两行数量相等扑克牌的取牌呢？

还真是报应，我在前一秒对那个女孩表示了鄙视之后，下一秒就看到那个和她眉目传情的家伙就是，我的男朋友，秦明。不过已经无所谓，因为下一刻，他就会被我称作，前男友。我在最后一刻还是犯了所有小女人都犯的矫情的毛病——我要和他在我们最初见面的地方说分手。

(学生一时理不出头绪，不知如何用符号化来表述问题，这时老师提示游戏中两行数量相等的扑克牌，这里扑克牌数量相等是不是一个具体的数呢？如何表示这个数呢？又如何表示每次取扑克牌的数量呢？在老师的这一启发下，学生想到用字母表示数，若设每行牌为a张，a为正整数，先取牌者第i次取ai张，后取牌者第j次取bj张，当i=j时，有ai=bj.)

师：刚才这个游戏对后取者有利，那么能否以扑克牌为背景设计一个游戏，对先取牌者利.

生6：如图5所示，一行5张，另一行7张，游戏规则不变.

图5

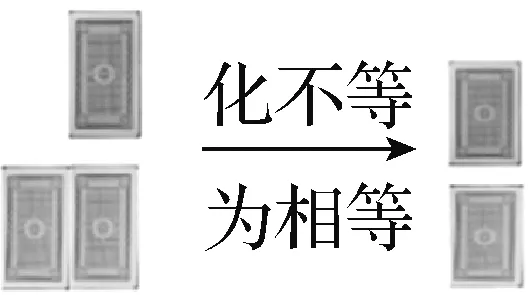
图6

师：说说你的理由？

生6：在图5所示的扑克牌中取走第二行中多余的2张牌，就化为两行数量相等，先取者就变成游戏2中的后取者.

师：还有不同的设计吗？

生7：一行5张，另一行6张，游戏规则不变.

师：先取者第一次应取几张牌？

师：刚才这两位同学分别给出两行为5、7张和5、6张，能否推广更一般呢？如“两行数量不等的扑克牌”，游戏规则不变，是否对先取者有利呢？

师：“两行数量不等的扑克牌”和刚才这两位同学分别给出两行为5、7张和5、6张，这两者有什么关系？

生(众)：是一般和特殊关系？

师：你们认为“两行数量不等的扑克牌”最特殊、最简单的是哪一种情形？

生(众):一行1张，另一行2张.

师：对于这种情况，先取者应如何取牌？

生(众):在一行2张牌中先取1张，化成二行各为1张(如图6).

师：对于一般情况，先取者又如何取牌呢？

生(众)：先取者在较多数量的一行中取走一些牌，使剩下的牌和较少一行数量保持相等，这样就转化为游戏2.

师：在上述两行数量相等或不等的扑克牌游戏中，你有什么收获或体会呢？

生7：当两行牌数量相等时，头绪比较乱，取一行扑克牌数量为1张，另一行为1张，这样有利于获得结论.

师：生7说得很好，为了简化问题，取特殊值，数学中把这种思想方法叫做特殊化思想.对于特殊化思想华罗庚曾说“ 善于退,足够的退,退到最原始而不失重要的地方,是学好数学的一个诀窍.”从中用数学的眼光看：做游戏和做数学题一样，都要善于特殊化.还有其它的感悟吗？

生8：做游戏和做数学题一样，都要善于转化，把陌生的游戏转化成熟悉的游戏.

生9：这些游戏的秘诀都是一方破坏数量相等，另一方重新建立新的数量相等从而达到新的平衡，使自己立于不败之地.

师：同学们都归纳得很好，当数量较多时首先要特殊化，首先把复杂问题简单化；其次学会转化的思想，把陌生的游戏转化成熟悉的游戏，这是最经济实效的方法；第三要用平衡的对称的思想去取牌.

点评：在学生充分理解游戏规则后，学生自主探究游戏.由于学生领会能力不一样，教师让各种不同观点的同学到讲台上进行操作演练，其它同学仔细观察并进行分析.为了让其它同学发现奥秘，老师有意控制牌的数量，慢慢的减少牌的数量，学生从中领悟到其中的奥秘.在解密“数量相等的扑克牌”游戏后，为了增强学生问题意识和培养提出问题的能力，教师让学生利用扑克牌自主设计“先下手有利，后下手不利”的游戏规则，很好地培养了学生提出问题能力.每一个游戏结束后，教师又注重对游戏操作过程的反思，学生在重复操作活动经验中，思维经历了从模糊到朦胧，从朦胧到清晰，学生做游戏的过程就是从无意识盲目地取牌到有点方法(特殊化)取牌，从有点方法取牌到有策略性地取牌，在重复操作和反思总结中不断优化学生的思维，提升学生数学思想方法.

1.3 游戏变式，深入探究

游戏3：如图7，用12张扑克牌摆成如下图所示的一个圆圈，甲、乙轮流从中取1张或2张牌，如果取走的是2张，这2张必须相邻，规定：取走最后一张牌者为胜.这个游戏的输赢和取牌的先后有关系吗？ 为什么？

图7

(在学生熟悉游戏规则后，然后分组演练，几分钟后，各小组的意见不一，在新的情景游戏中许多学生未能很好迁移上述游戏中解决的策略，如特殊化思想、化归思想、对称思想.教师通过比较上述游戏中的相同点和不同点，从而启发学生解决问题的策略)

师：这个游戏跟以上我们刚刚玩过的有类似吗？

生(齐)：有.

师：那些类似呢？

生10：都是取最后一张牌者为胜.

生11：不同点是这一次取牌仅取1张或2张，取2张时，这2张必须是相邻的，而上述游戏每次在一行中可以任意取多少张.

师：这两位同学都从游戏规则上加以总结，还能否从其它角度去思考吗？比如从取牌的策略和方法上.

师：上述游戏2用到哪些数学思想方法？

生12：从特殊到一般，转化思想，对称地取牌

思想等.

(这时，一位同学突然有所感悟，举手示意)

生13：这个游戏对后取者有利.

师：为什么？

生14：先特殊化，当牌为2张时，如图8所示，先取者取完2张就赢了；当牌为4张时，如图9，先取者只要取一张，此时后取者无论如何取1或2张牌，都留下2或1张，同样也是先取者为赢.因此我猜想，偶数张扑克牌，先取者赢.

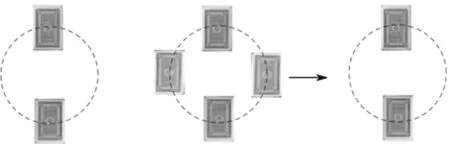
图8 图9 图10

师：刚才这位同学利用上面玩游戏的经验，对牌的数量进行特殊化，从而得出猜想对先取者有利.对生14同学的想法，其它同学有不同的想法吗？

生15：不对，当牌的数量为4张时，对先取者不利，当先取者取1张时，后取者在其正对面取1张(如图9到图10)，留下2张，但这2张不是相邻的牌，由于规则中“若取2张牌必须是相邻的”，就相当于两行各1张牌，转化成上述两行数量相等，由上述游戏可知先取者输；当先取者取2张，后取者也取2张，总之，对先取者不利.

师：生15注重对游戏规则的解读，并指出4张牌时，对后取者有利.现在牌为12张时，还是对后取者有利吗？

生16：后取者有利，理由如下：在图11中，当先取者取一张牌时，后取者在其正对面也取1张，如图12，转化成两行数量相等的牌；若当先取者取2张时，后取者在其正对面也取2张，如图13，也转化成两行数量相等的牌.

图11

图12

图13

师：在12张圆形扑克牌中，后取者只要和先取者关于圆心对称地取牌(如图12)，这样剩下的扑克牌在形式上转化为数量相等的两行牌，然后只要后取者保持与先取者呈对称地取牌就可.如果把12张扑克牌改成13张扑克牌，其它不变那么还是后取牌者有利吗？

图14

图15

(学生慢慢学会以退为进，当3张牌时，通过特殊化的方式加以猜想得到结论：“对后取者有利”；师生在特殊中总结经验，增加牌的数量，利用上述游戏对称的取牌策略，化图14为图15，即当先取者取2张牌时，后取者在其正对面取1张牌，把圆形的扑克牌转化成两行数量相等的扑克牌.)

师：在这个游戏的玩耍中，你们又有怎样的体会？

生17：当你思考问题没有头绪时，要善于把问题简单化、特殊化.

生18：感受最深的是要学会转化，把陌生的转化成熟悉的，把做不来转化成已会的.

师：上述游戏的形式虽变，但解决游戏策略和方法却没有变.如化繁为简的特殊化思想，化生为熟的转化思想等，却是解决游戏关键所在.

点评：游戏2中“从两行数量相等”的扑克牌游戏到学生自主设计“两行数量不等”的扑克牌游戏，再到游戏3中“偶数张”扑克牌到“奇数张”扑克牌，扑克牌排列的形状从线性到非线性，取牌策略和思维从易到难，问题层层递进，后一个游戏都是前一个游戏螺旋往复上升，符合学生的认知.通过这样一组变式游戏训练，使学生重复性经历了相同的数学活动经验，并把这种同一经验的数学活动应用到不同背景的游戏中去，在这一过程中积累更一般、更有效、更抽象的数学活动经验，这样用相同的经验和方法去做不同的事情，是活动经验上升到数学思想方法关键所在.

1.4 破解游戏，迁移方法

(再回到本节课的开头吹“蜡烛游戏”，学生通过对游戏3和“蜡烛游戏”进行比较，发现“吹蜡烛游戏”其实质是游戏3中牌的数量从12张推广到18张，后吹者为了确保胜出，如图16，后吹者乙只要在先吹者的对面吹灭相同数量蜡烛，图17把它分成两行数量相等的燃着蜡烛就转化成游戏2.)

图16

图17

师：上述的诸多游戏虽精彩纷呈，但游戏背后思想方法却是相同，如果把这种思想方法运用到数学解题中去，那么解数学题就如同玩游戏.

点评：“吹蜡烛”游戏问题的提出到最后解决“吹蜡烛”游戏，前后呼应，高潮迭起，学生在游戏2、3中重复经历同一活动经验，并在反思中抽象为一种游戏的策略和数学思想方法，到最后又一次通过真实的吹蜡烛游戏体验，来检验有效的活动经验和游戏的策略，并同时把这种有效的数学思想方法和策略迁移到数学解题中去，在解决问题中变得更方便、更简约、更有效，在解决问题过程中，学生不仅学会了学习，学会了方法，而且也品味到数学的乐趣和魅力.

2 进一步思考的问题

(1)游戏进一步变式

就本节课而言，游戏3还可以进一步变式并进行推广.

推广之一，游戏问题一般化，从原来的12张扑克牌变成n张牌围成一个圆圈，例如“n张扑克牌围成一个圆圈，甲、乙轮流从中取m(1≤m≤n)张,且这m张必须相邻…”

推广之二，取消m张扑克牌相邻的位置为任意位置，其它不变.

推广之三，改取扑克牌为放扑克牌，如“甲、乙轮流交替向一张长方形的桌子上放扑克牌,每次放一张且牌全落在桌子内部，每张牌必须平放且不准重叠.规定：放下最后一张扑克牌即为胜者.”

或许推广后的扑克牌游戏，思维会朝向纵深处发展，学生拓展的空间和潜能会更大.

(2)游戏可进一步抽象化

游戏2和游戏3博弈的策略是数量对称性地取牌，还可以进一步抽象化，例如游戏2中，可以把每一张扑克牌抽象一个点，设每行相等点的数量为n，甲、乙轮流从中取牌，设甲的取牌为a1,a2,…,am,乙的取牌为b1,b2,…,bm,游戏2中后取者乙为了获胜，则有a1=b1,a2=b2,…am=bm,这样就得到a1+a2+…+am=b1+b2+…+bm=n.同样游戏3也可以抽象成数.如果课堂中从数的层面领会取牌，更能领会到游戏的本质.