第二十届北京高中数学知识应用竞赛决赛试题及参考解答

2017年3月26日

一、下图是只印有月、日及星期的年历．

(1)这份2017年的年历最早能在公元哪一年再次使用？请说明理由．

(2)这样的公元2016年(闰年)的年历，最早能在公元哪一年再次使用？请说明理由．

解(1)2023年，(2)2044年．

理由如下：

(1)因为2017、2018、2019、2021、2022、2023年都是非闰年，每年365天，365≡1(mod 7)，而2020年是闰年，366≡2(mod 7)．这样从2017年元旦到2022年12月31日，正好经过7的倍数天数，因此2023的年历与2017年的年历中日、月、和星期的信息一样，这一年是最早可以再次使用2017年历的．

(2)2016年是闰年，和它一样的年历也必须是闰年．而每一个闰年周期是4，3×365+366=1461≡5(mod 7)，而5和7是互质的，因此，经过7个闰年周期,即28年，年历中的日、月和星期的信息与2016年一样的，这一年是2044．

二、罗盘经纬仪是一种工程测量仪器，如图．其中的罗盘用于测定东西南北方向的方位，经纬仪视筒可以水平或竖直旋转，通过刻度盘读出视线的水平或垂直旋转角度．它适用于农田水利、土地规划、地形规划、地形测绘等一般的工程测量．今使用罗盘经纬仪分别从观测点A1(-120.4°W, 48.6°N)、A2(-120.6°W, 48.6°N)，(括弧中的一组数量表示的是西经、北纬的度数)观测目标点S，这两条视线的方位角(视线与正北方向的水平夹角)分别为242°和 198°．如果过A1、A2和S这三点的平面可以近似地表示地球的表面．求点S的经纬度．

解建立以经度，纬度为坐标的直角坐标系，如下图。取平行于纬线的直线为横轴(x轴)，正东方的指向为正向．平行于经线的直线为纵轴(y轴)，正北方向的指向为正向．通过点A1(x1,y1)、A2(x2,y2)观测目标S的视线分别为过A1、A2点的直线，与纵轴的夹角分别为α1和α2．他们相交于目标点S(x,y) ．

由此可以得到这两条直线的点斜式为

y-yi=cotαi(x-xi),i=1,2，

即

y-(cotα1)x=y1-(cotα1)x1

y-(cotα2)x=y2-(cotα2)x2

即

(sinα1)y-(cosα1)x=(sinα1)y1-(cosα1)x1

(sinα2)y-(cosα2)x=(sinα2)y2-(cosα1)x2

将数据(x1,y1)=(-120.4°W, 48.6°N)、(x2,y2)=(-120.6°W, 48.6°N)和α1=242°，α2=198°带入模型中，求解得到

(x,y)= (-120.64°W, 48.47°N) ．

三、一辆小汽车在普通路面上行驶，测得一组数据，见下表(表1)

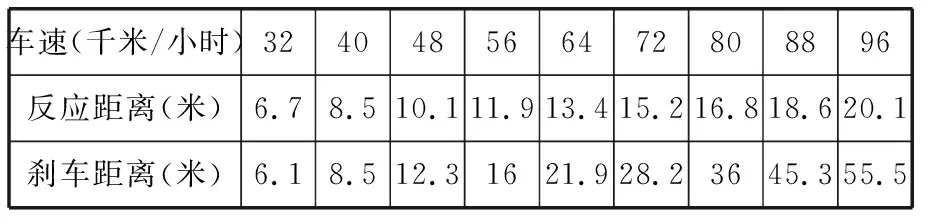
车速(千米/小时)324048566472808896反应距离(米)6.78.510.111.913.415.216.818.620.1刹车距离(米)6.18.512.31621.928.23645.355.5

其中反应距离是指从驾驶员做出反应动作到刹车制动开始起作用这段时间内汽车行驶的距离；刹车距离是指从刹车制动开始起作用到汽车完全停止这段时间内汽车行驶的距离．请以这组数据回答下面问题：

(1)对于这个小汽车和这个驾驶员，建立反应距离关于车速的函数模型。

(2)对于这个小汽车和这个驾驶员，建立刹车距离关于车速的函数模型。

(3)若十字路口最大限速为v=50千米/小时，路口宽度为30米，如果只考虑小轿车的通行安全，并以表1为依据，那么信号灯的黄灯至少要亮多少时间？

解设驾驶员反应时间为t，反应距离为s1，刹车距离为s2，车速为v．

车速(千米/小时)324048566472808896t(秒)0.75380.76500.75750.76500.75380.76000.75600.76090.7538

由此表可见，反应时间非常接近，t的均值= 0.7584，方差= 2.0927×10-5．于是，将反应时间设为常数0.7584是合理的．

反应距离关于车速的函数模型为s1=0.7584v．

车速(千米/小时)32404856647280889612a(秒2/米)0.07720.06890.06920.06610.06930.07050.07290.07580.0780

(3)因为最大限速为50千米/小时(约为13.88米/秒，从安全角度考虑，可近似为14米/秒)，路口宽度(记作m)为30米，黄灯亮的时间应该允许离停车线距离小于停车距离(s2+s2)的汽车开过十字路口，而

s1(14)= 0.7584×14=10.6176(米)，s2(14)= 0.072×142=14.112(米)．

根据匀速运动规律，有

所以，信号灯的黄灯至少要亮4秒．

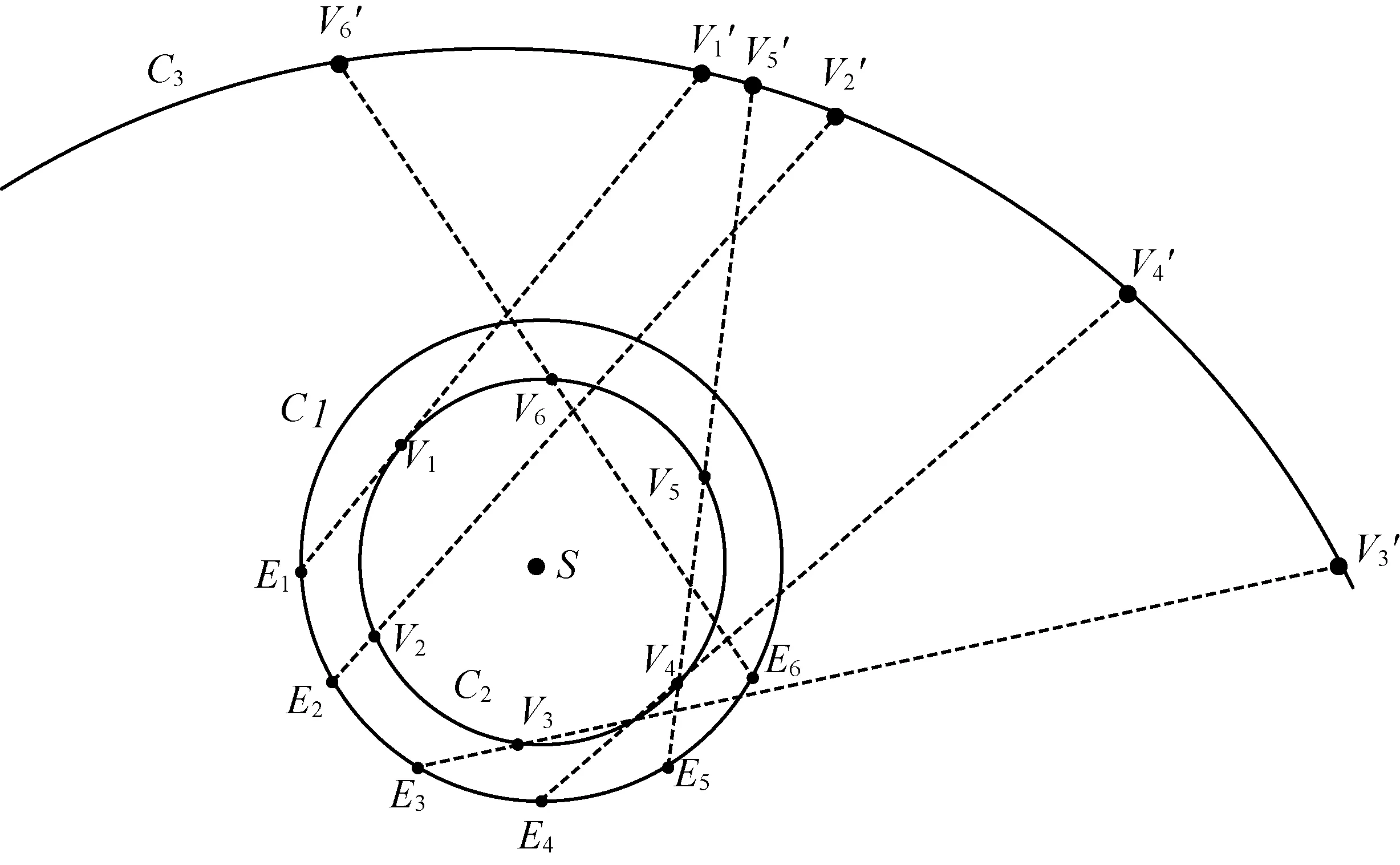
四、1543年哥白尼发表《天体运行论》提出了日心体系，目前普遍认定太阳系八大行星都绕着太阳做圆周运动．其中，水星和金星的轨道半径比地球的小，称为内行星；火星、木星、土星、天王星和海王星的轨道半径比地球的大，称为外行星．那么，在地球上观察其它行星的运动时，会看到它们有时“前进”，有时“后退”．例如，通过连续的若干天观察，发现金星在天空中的位置是由左向右移动(顺行)，接下来若干天又是由右向左移动(逆行)，较长时间观察会发现，金星在天空呈“顺行→逆行”循环的变化规律．

请借助下图，在图上进一步标记出运动中的地球、金星的位置，解释金星在天空呈“顺行→逆行”的变化规律．

(为了方便分析，在不影响对运动变化规律分析的前提下，设金星轨道半径等于地球轨道半径的四分之三(实际约为0.723)，金星公转角速度等于地球公转角速度的2倍(实际约为1.626))．

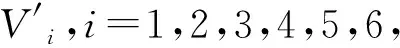
五、现有一条较长的等间隔地串连在一起的彩灯链，其中有一个灯泡坏了，致使链上的彩灯都不亮了．如果我们手里有完好的导线，可以用“二分法”将坏灯泡排查出来． 步骤如下．

第一步：将有坏灯泡的彩灯链记为AB，完好的导线记为CD，将AB连接到电路中后，再将C连到A处，D连到AB的中点M处．

第二步：如果MB段灯泡亮，则表明坏灯泡在AM段上，这时我们排除掉MB段，并且将M改记作B，对新的AB段重复第一步的过程；如果彩灯MB段灯泡不亮，则表明坏灯泡在MB段上，这时我们排除掉AM段，并且M改记作A，对新的AB段重复第一步的过程．

第三步：重复上面两步，直到找到坏灯泡为止．

对上述排查步骤，一名学生有如下观点：

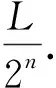
请你通过计算n次“第一步”之后所得包含坏灯泡的区间长度都可能取哪些值和分别对应的概率，比较“取中点”和“取三等分点”策略的优劣．

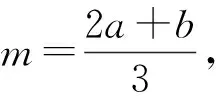
据此，得到离散型随机变量Ln的概率分布列为：

Ln13 n(b-a)13 n-123 (b-a)…13 n-k23 k(b-a)…23 n(b-a)PC0n13 nC1n13 n-123 …Ckn13 n-k23 k…Cnn23 n

于是，随机变量Ln的数学期望为

这表明，在平均意义下，n次“第一步”之后，“取三等分点”法所得包含坏灯泡的区间长度期望更大一些，没有“取中点”的精度高．

从而“取中点”比“取三等分点”的策略更好一些．