利用矩阵分析一个向量序列的收敛性

管 涛 范兴亚

(1.中国人民公安大学信息技术与网络安全学院102600 2.北京市第四中学数学组 100037)

我们知道，利用矩阵可以求解斐波那契类型的递推数列的通项公式. 事实上很多递推问题都可以利用矩阵解决. 我们来看下面这样一个有趣的数学游戏：一个正方形，画出它的中点正方形；再画出新正方形的中点正方形，依此类推，会生成一个漂亮的图案. 如果在原正方形的四个顶点处随意各写一个自然数，将相邻顶点处的自然数相减(用较大的数减较小的数，若两数相等，则差为0，称这种运算为相邻做差运算)，计算结果写在每条边的中点；依此类推.

例如：最先写下2、12、15、8，运算1次后得到10、3、7、6，运算2次后得到7、4、1、4，运算3次后得到3、3、3、3，运算4次后得到0、0、0、0. 如下图：

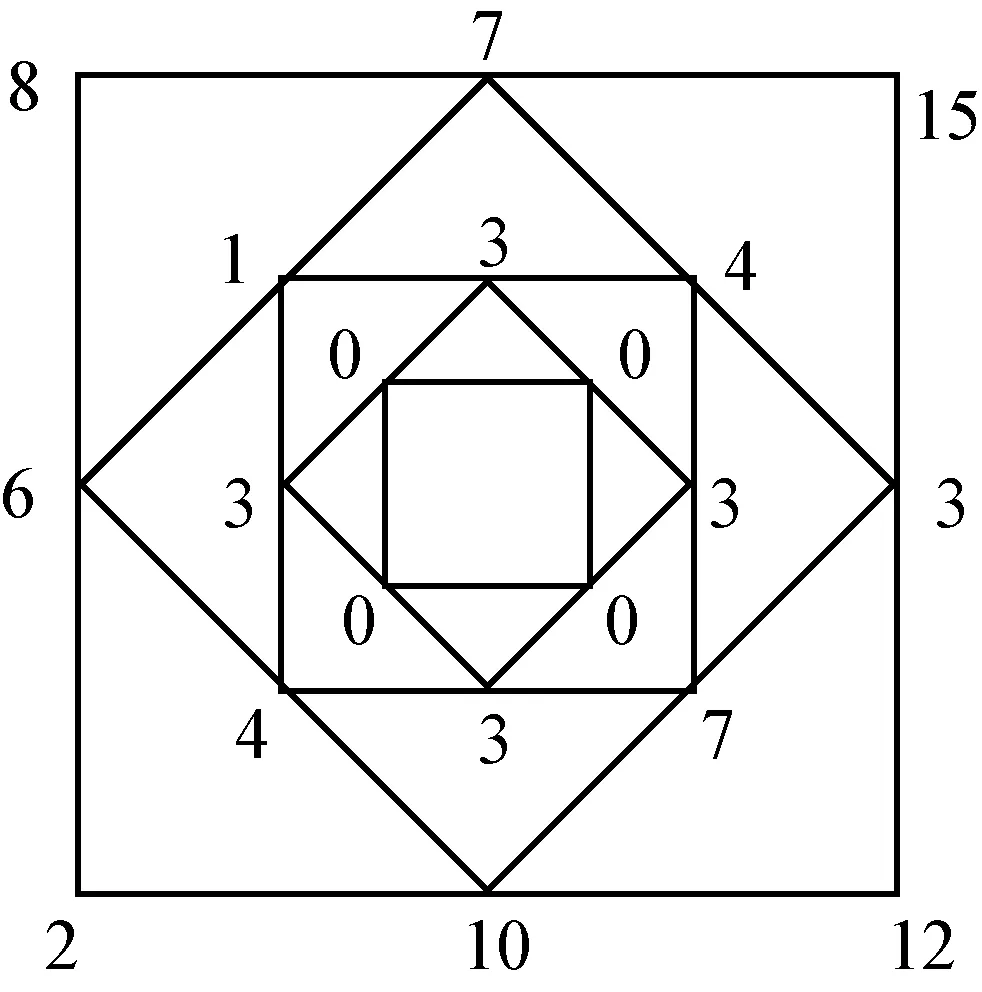
如果我们重复几次这样的游戏，就会发现不管开始写下什么数，似乎最后总会化为0. 因此可以猜想对于正方形进行相邻做差运算，最终一定会化为四个数都是0的状态. 这一猜想是否正确？如果把正方形换成正n边形，又会有什么样的结论呢？

更一般的，我们可以借助向量序列的概念来描述这一问题.

问题1如下定义n维向量序列.α1=(a11,a12,…,a1n)中的元素都是自然数，当i≥2时，向量αi=(ai1,ai2,…,ain)中的元素aij=|ai-1,j-ai-1,j+1|，其中规定ai-1,n+1=ai-1,1.在上述定义下，向量αi是否会收敛到零向量？

换句话说，令max{ai1,ai2,…,ain}=Ai，数列{Ai}是否会在有限步之内收敛到零？答案是否定的，但是我们可以得到如下的性质.

性质1{Ai}极限一定存在，可设其为A，而且必定在有限步内收敛到其极限值A.

证明根据定义易知Ai≤Ai-1，也就是数列{Ai}单调减(非严格单调减)，又因为{Ai}非负，根据单调有界准则[1]，{Ai}必有极限值A. 又因为任意aij都不大于A1，因此向量αi只有有限多种不同的形式，迟早会进入周期循环状态，那就是说{Ai}必定会在有限步之内达到A并在之后保持恒定.即存在某个下标k，当i≥k时，Ai恒等于A. 证毕.

但是A并不一定等于零，它也有可能是一个正整数. 例如当n=3时，令α1=(a11,a12,a13)=(1,1,0)，那么α2=(a21,a22,a23)=(0,1,1)，可看作是(a11,a12,a13)中的元素做了一个3轮换，如果作为环排列写在正三角形的三个顶点，则等同于(a11,a12,a13)，此后必然是一个周期为3的循环状态，所以A=1. 那么很自然的会想到如下问题.

问题2当n取何值时Ai必然收敛到零.

为解决问题2，我们需要进行较复杂的推理和分析. 我们已经知道，存在下标k，使得当i≥k时Ai恒等于其下限也就是极限值A. 接下来分析在此之后的向量αi中的元素可以取哪些自然数？

性质2当i≥k即Ai已经达到其下极限A时，ai1,ai2,…,ain只能取0或A.

证明设当i=k时，Ai已经达到其下极限A. 那么在ak+n-1,1,ak+n-1,2,…,ak+n-1,n中存在至少一个元素等于A，不妨设ak+n-1,1=A. 逆推回去，ak+n-2,1和ak+n-2,2必然一个是0一个是A，再继续逆推，ak+n-3,1、ak+n-3,2和ak+n-3,3也必须都取值0或A，并且至少有一个是A. 依此类推，ak1,ak2,…,akn全都要取0或A，因此对所有的i≥k以及有意义的j，aij都等于0或A. 证毕.

假定A为正数，那么不妨设A=1. 为解决问题2，我们只需对n维的0-1向量进行讨论，搞清楚当n取何值时，任意0-1向量一定会在有限步内化为零向量.

由于向量中的元素只取0和1，问题1中的递推公式也可以等价的描述为问题3.

问题3如下构造定义在2元域F2={0,1}[2]上的n维向量序列.首先任给α1=(a11,a12,…,a1n)，当i≥2时，令向量αi=(ai1,ai2,…,ain)中的元素aij=ai-1,j+ai-1,j+1，其中规定ai-1,n+1=ai-1,1. 当维数n取何值时，一定存在某个下标k使得αk=0.

问题3也可以用2元域F2上的矩阵进行表述，设n阶方阵

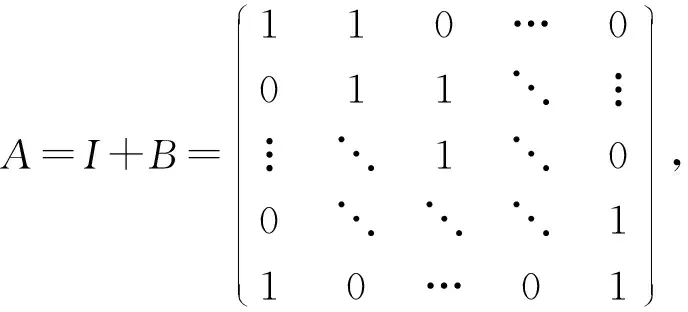
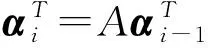
首先给出一个引理.

证略. 读者可自行阅读参考文献[3]中75页习题31的解答.

借助引理1能得到下述结论.

定理1当n=2m时，A作为2元域F2上的矩阵是幂零的，An=0.

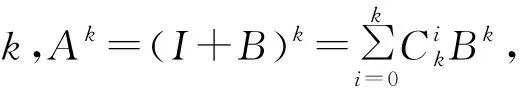
所有元素均为偶数，因此在A是2元域F2上的幂零矩阵. 证毕.

由定理1容易推出，当n=2m时，按上述定义的任意n维0-1向量，至多经过n次相邻做差运算就可以得到零向量. 再进一步得到下面的性质3.

性质3当n=2m时，在正n边形的每个顶点上随意写一个整数，进行相邻做差运算，经过有限步后一定会化为都是0的形式. 文章最初正方形的问题作为性质3的一个特例也随之解决.

为了考虑n不是2的幂时的情况，我们需要借助Hamilton-Cayley定理.

引理2(Hamilton-Cayley定理)数域F上，方阵的特征多项式一定是零化多项式.

证略.

在F2中考虑A的特征多项式f(λ)=|λI-A|=(λ-1)n+(-1)n-1. 当n=2m时，特征多项式可化为λn，由此也可得到前面定理1的结论. 当n不是2的幂时，在f(λ)=(λ-1)n+(-1)n-1是一个至少含有两项的n次多项式，并且其常数项为0.

定理2当n不是2的幂时，A作为2元域F2上的矩阵不是幂零的.

证明在F2中考虑矩阵B的特征多项式g(λ)=|λI-B|=λn+(-1)n-1=λn+1，由引理2可知g(B)=0. 而对于任意次数小于n的m次多项式h(λ)，h(B)中第1行第m+1列的元素非零，因此g(λ)也是矩阵B的极小多项式.

下面考虑矩阵A的极小多项式，由于B=A-I，因此A的特征多项式

f(λ)=g(λ-1)=(λ-1)n+1=(λ+1)n+1

也就是A的极小多项式.

当n不是2的幂时，根据引理1可知，将f(λ)展开后除λn以外至少还有一项，即f(λ)不是单项式. 因此对任意正整数i，单项式λi都不能被f(λ)整除，这意味着λi不是A的零化多项式，所以A不幂零. 同时这也说明对任意的i，总能找到0-1向量γ使得Aiγ≠0. 证毕.

在定理2的证明中，我们已经得到了如下性质，

性质4当n不是2的幂时，在正n边形的每个顶点上随意写一个整数，进行相邻做差运算，有可能无法化为都是0的形式，而是陷入循环，这个循环中只出现0和某个正数A.

例如，在正六边形的顶点写下9、5、2、6、9、6，经过一次相邻做差运算后变为4、3、4、3、3、3，继续做下去，得到的结果如下表

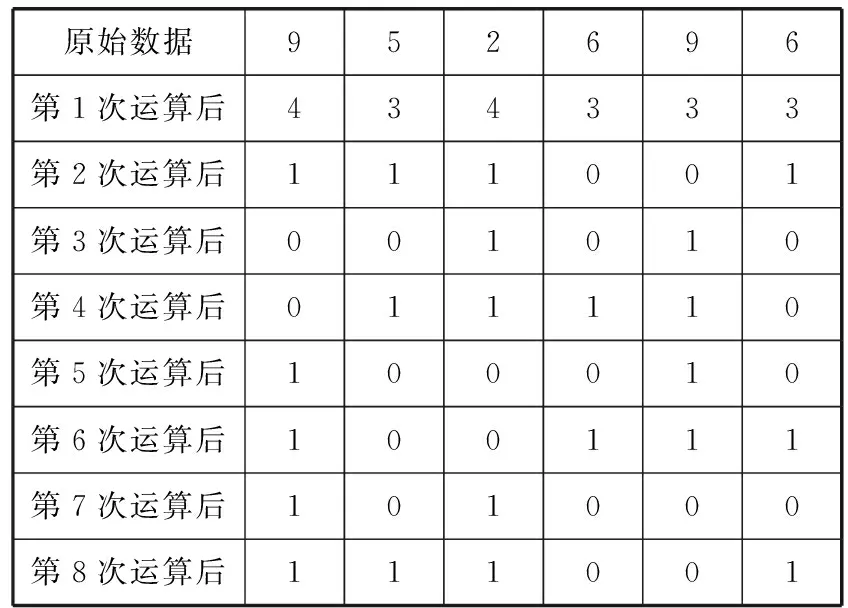
原始数据952696第1次运算后434333第2次运算后111001第3次运算后001010第4次运算后011110第5次运算后100010第6次运算后100111第7次运算后101000第8次运算后111001

第8次运算结果和第2次运算结果相同，从此开始循环，循环周期为6.

这样我们完全搞清楚了正n边形上的相邻做差运算产生的向量序列的收敛性问题. 当然其中还有很多定量计算的东西值得进一步探讨. 例如任给一个2m维的向量，能否计算出它收敛到0所需要的步数；再比如，当维数不是2的幂时，循环的最小正周期是多少. 希望本文能起到抛砖引玉的作用，让各位读者进一步思考并解决这些问题.